Iteration
... ist ein Verfahren, bei dem ein bereits gewonnenes (Zwischen)ergebnis wieder den Startwert für den nächsten strukturell gleichen Rechenschritt bildet:
Eine Funktion f wird auf z0 angewendet, f(z0) ist dann der neue Startwert und es wird nun f(f(z0))=f2(z0) berechnet usw.
Die Iterationsfolge kann beschränkt sein oder auch divergieren.
Ein Beispiel für eine solche Rechenvorschrift ist das Heronsche Wurzelziehen oder das Näherungsverfahren von Newton-Raphson zur Nullstellenbestimmung.
Affine Abbildungen: 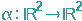
Bildet man eine Ebene auf sich selbst ab und ist diese Abbildung umkehrbar und geradentreu, so heißt sie affine Abbildung.
Geraden, Parallelität und Teilverhältnisse bleiben dabei erhalten, Längen und Winkel i. a. jedoch nicht.
Die zugehörigen Abbildungsgleichungen können dabei in Vektorschreibweise, in Koordinatenschreibweise oder in Matrizenschreibweise dargestellt werden:
Beispiel: Der Punkt P(3/5)=P(x1/x2) werde auf den Punkt P'(5/11)=P'(x1'/x2') abgebildet, die ff. Vektoren seien gegeben:
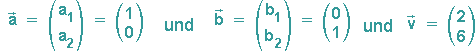
Dann gilt: 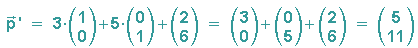
Die Vektorschreibweise der affinen Abbildung:
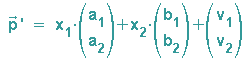 ,
,  und
und  linear unabhängig.
linear unabhängig.
Beispiel: Der Punkt P(3/5) = P(x1/x2) werde auf den Punkt P'(5/11)=P'(x1'/x2') abgebildet:
Dann gilt:
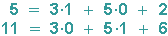
Die Koordinatenschreibweise der affinen Abbildung:
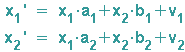
Beispiel: Der Punkt P(3/5) = P(x1/x2) werde auf den Punkt P'(5/11)=P'(x1'/x2') abgebildet.
Gegeben sei der Vektor  und die Matrix A.
und die Matrix A.
-
Einschub Matrix A = (aij):
Eine mxn-Matrix ist ein Zahlenschema, das aus m Zeilen und n Spalten besteht
Dann ergibt das Produkt der mxn-Matrix mit einem Vektor, der n Komponenten hat, wieder einen Vektor mit n Komponenten:
Für das i-te Vektorelement des Ergebnisvektors gilt dabei:
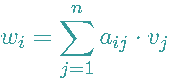
Es gilt dann:
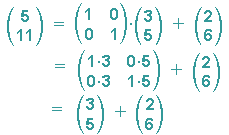
Die Matrizenschreibweise der affinen Abbildung:
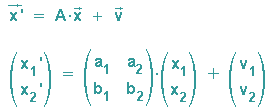
Gebrochene Dimension (Fraktaldimension)
Die Idee, den Begriff "gebrochene Dimension" einzuführen, stammt von Felix Hausdorff.
Zunächst eine Vorüberlegung:
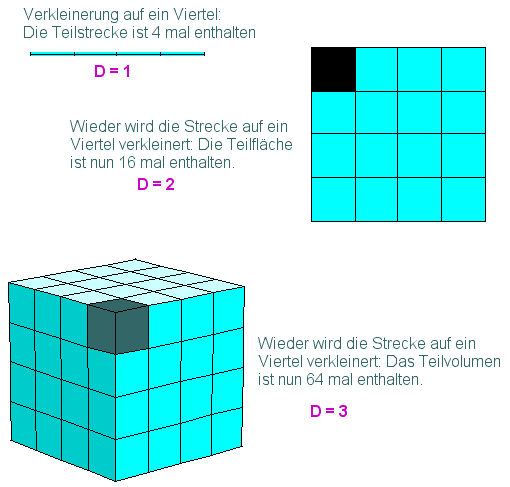
Für alle 3 Abbildungen ist der Streckfaktor= Bildlänge : Originallänge = 0.25, der Verkleinerungsfaktor s ist also der Kehrwert davon: s=4.
Es sei nun a = Anzahl der Objekte nach Verkleinerung der Strecke. Dann gilt:
| Nr. der Abb. | Dimension | Verkleinerungs - faktor s | Anzahl a der Objekte n.Verkleinerung | Formelzusammen - hang |
| 1. Abb. | D = 1 | s = 4 | a = 4 | 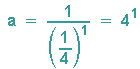 |
| 2. Abb. | D = 2 | s = 4 | a = 16 | 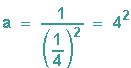 |
| 3. Abb. | D = 3 | s = 4 | a = 64 | 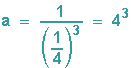 |
Sieht man sich den jeweiligen Formelzusammenhang an, so erkennt man:
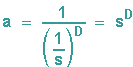
Da ja nun der Begriff "gebrochene Dimension" erläutert werden soll, ist es ungünstig, dass ausgerechnet D als Hochzahl auftaucht, kein Problem für all diejenigen, die sich noch an die Logarithmen aus Klasse 10 erinnern, wir schreiben diese Gleichung einfach um:
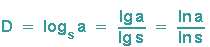
... und haben schon mal die Möglichkeit gewonnen, die Dimension eines Fraktals sinnvoll zu definieren:
Die Vorüberlegung hat uns zu einer Formel geführt, mit der wir nun die Dimension des Sierpinski-Dreiecks bestimmen:

Die Seitenlänge des Dreiecks wird halbiert, also 1:Streckfaktor=s=2.
Da das mittlere kleine Dreieck jeweils entfernt wird, haben wir nach der Verkleinerung noch 3 Objekte, also a=3.
Die Dimension des Sierpinski-Dreiecks wird also sinnvollerweise wie folgt festgelegt:

... und aus ist's mit den ganzzahligen Dimensionen aus der euklidischen Geometrie, wir haben eine "gebrochene Dimension"!
Sehen wir uns noch ein weiteres Beispiel an, den Cantor'schen Staub - auch Cantor-Menge genannt (Georg Cantor, Begründer der Mengenlehre, 1845 - 1918):
Die Erzeugungsregel der Cantor-Menge: Nehme eine Strecke und entferne aus ihr das mittlere Drittel:

Nach n-maliger Anwendung der Erzeugungsregel hat man also 2n Teilstrecken, wobei die Summe deren Längen jedoch (2:3)n ist und der zugehörige Limes für n gegen unendlich also 0 ist.
Hier ist s=3 und a=2, bei Anwendung unserer Formel ergibt sich die Dimension D=0,63093.... , schon wieder eine gebrochene Dimension.
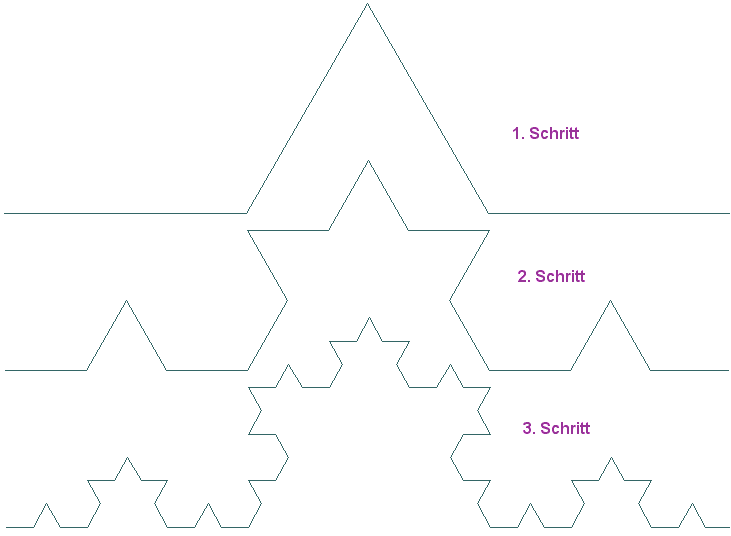
Und zum Schluss noch eine kleine Aufgabe:
Ersetze in einem gleichseitigen Dreieck das mittlere Drittel jeder Seite durch eine Spitze, deren Seitenlängen diesem Drittel entprechen, führe dies mehrmals für ein gleichseitiges Dreieck durch und Du erhältst die Kochsche Schneeflocke (Helge von Koch, schwedischer Mathematiker, 1870-1924). Bestimme ihre Dimension ... Dein Ergebnis sollte 1,26186... betragen.
Fixpunkt und Fixpunktgleichung
Fixpunktgleichung: Ein Wert x, der die Gleichung f(x) = x erfüllt, d.h. der durch die Anwendung der Funktion f unverändert bleibt, heißt Fixpunkt.
Sei f(x)=x2. Es ist f(1)=1, 1 ist also Fixpunkt.
Nicht nur für Zahlen, sondern auch für "echte" Punkte gilt diese Aussage.
Abbildung DREHUNG: Das Drehzentrum ist Fixpunkt.
Bewege mit gedrückter Maustaste die Ecke Ai des Dreiecks. Beim linken Dreieck ändern sich die Koordinaten aller Punkte der Dreiecksfläche, beim rechten Dreieck ist das Drehzentrum Fixpunkt, solange es innerhalb des Dreieckes liegt.
Winkel und Längen der Strecken bleiben erhalten.
|
|
Abbildung ZENTRISCHE STRECKUNG: Das Zentrum ist Fixpunkt. Winkel und Längenverhältnisse bleiben erhalten.
Bewege mit gedrückter Maustaste die Ecken des Vierecks oder den Schieberegler s.
|
|
Kombiniert man also eine Drehung mit einer Streckung, so bleiben folglich wie bei der zentrischen Streckung die Längenverhältnisse und Winkel erhalten.
Mit Würfeln und ein bisschen Zeit zum Sierpinski-Dreieck
Die Idee stammt von Jürgen Giesen: Vortrag "Chaosforschung - Fraktale - Chaos - Ordnung" . Der Vortrag ist auch für EinsteigerInnen sehr gut verständlich.
Ein Applet zum Würfelspiel findet man hier.
Die Spielregel:
- Wähle in einem großen gleichseitigen Dreieck ABC einen Startpunkt S0.
- Du würfelst 1 oder 2: Gehe die halbe Streckenlänge SA in Richtung A und benutze nun diesen Punkt als Startpunkt S1.
- Du würfelst 3 oder 4: Gehe die halbe Streckenlänge SB in Richtung B und benutze nun diesen Punkt als Startpunkt S1.
- Du würfelst 5 oder 6: Gehe die halbe Streckenlänge SC in Richtung C und benutze nun diesen Punkt als Startpunkt S1.
- Wiederhole diese Regel möglichst oft.
Du erwartest, dass die Zielpunkte mehr oder weniger gleichmäßig
über das Dreieck gestreut sind? Weit gefehlt! Es entsteht ein Muster:
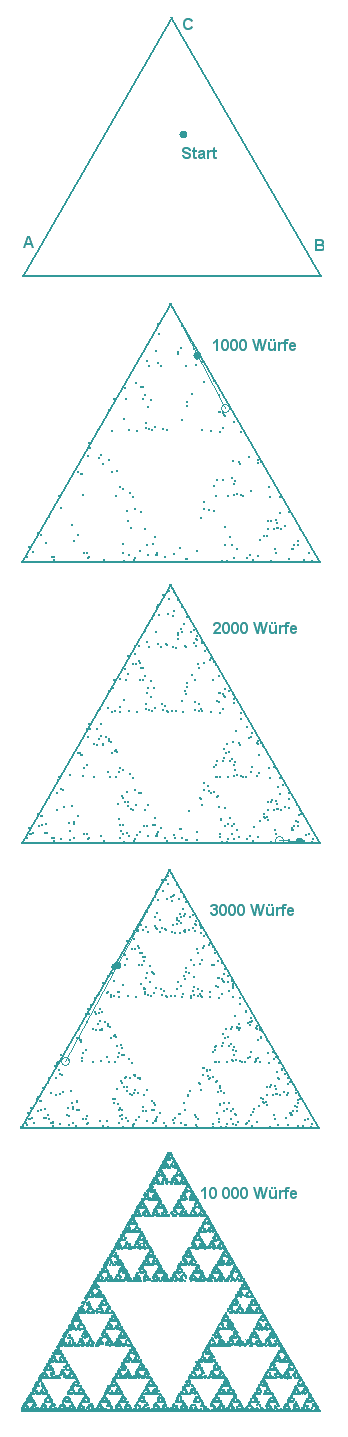
Waclaw Sierpinski (polnischer Mathematiker, 1862 - 1969) hat dieses Dreieck, das schon als Muster z.B. in der romanischen Kathedrale von Anagni benutzt wurde, ausführlich beschrieben:

Verwendet man die Erzeugungsregel "Nehme ein gleichseitiges Dreieck, teile es in 4 flächengleiche Dreiecke, nimm das mittlere heraus, und wiederhole diesen Vorgang mit den Teildreiecken", dann entsteht eine exakt selbstähnliche Form, ein "Fraktal" (der Begriff wurde von Benoit Mandelbrot (französischer Mathematiker polnischer Herkunft, geb. 1924, Mitbegründer der Chaostheorie) eingeführt).

Es hat eine "gebrochene Dimension". Siehe auch hier.
Strahlensätze
Von einem Punkt S gehen zwei Strahlen aus, die von 2 Parallelen geschnitten werden.
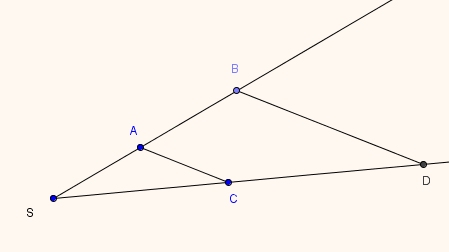
Für diese sog. Strahlensatzfigur gilt dann (wg. Ähnlichkeit der entsprechenden Dreiecke):
Die Längen der Abschnitte auf dem einen Strahle verhalten sich wie die entsprechenden Längen der Abschnitte auf dem anderen Strahl:
SA : SB = SC : SD
Die Längen der Abschnitte auf den Parallelen verhalten sich wie die Längen der Abschnitte der vom Scheitelpunkt S aus gemessenen entsprechenden Abschnitte:
SA : SB = AC : BD
und
SC : SD = AC : BD
Hier nochmal eine Übersicht über die Strahlensätze im Internet.
Asymptote
Betrachtet man z. B. die gebrochen rationale Funktion
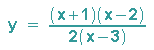
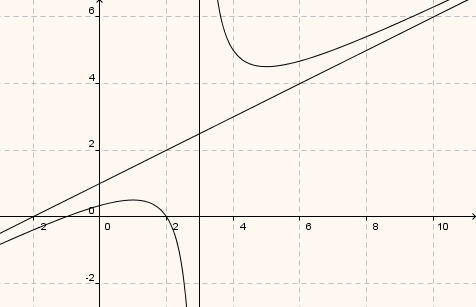
und untersucht ihr Verhalten für x gegen +/- unendlich, dann kann man im Funktionsterm den ganzrationalen Term abspalten:
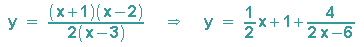
und erkennt, dass der Wert des Bruches für diesen Fall gegen Null strebt. Die verbleibende Gerade wird Asymptote der Funktion genannt. Manchmal wird auch noch die Polstelle x=3 so genannt.
| © 2009-2024 Asti | PoVRay-Site |