Komplexe Zahlen
Im Bereich der reellen Zahlen ist die Gleichung x2 = -1 nicht lösbar. Was können wir tun?
Erinnern wir uns zunächst an Addition, Subtraktion und Multiplikation reeller Zahlen am Zahlenstrahl:
Addition und Multiplikation positiver reeller Zahlen: 3+3=6 und 2.3=6
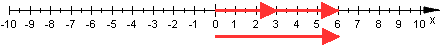
Soll die 3 mit -2 multipliziert werden, dann kommt eine Drehung um 180° dazu:
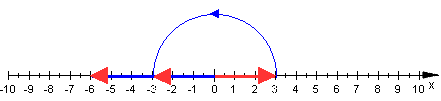
Gehen wir zurück zu unserer Gleichung x2=-1. Wir suchen eine Zahl, die mit sich selbst multipliziert, -1 ergibt. Wir nennen diese Zahl i.
Es soll also gelten: i . i = -1
Die zweimalige Multiplikation mit i soll der Multiplikation mit -1 entsprechen, d. h. einer Drehung um 180° am Zahlenstrahl, also muss die einmalige Multiplikation mit i einer Drehung um 90° am Zahlenstrahl entsprechen.
Wir erhalten also die folgenden Darstellung:
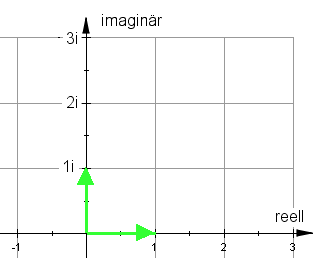
Setzt sich eine komplexe Zahl nun aus einem Real- und einem Imaginärteil zusammen, dann wird sie als Zeiger dargestellt:
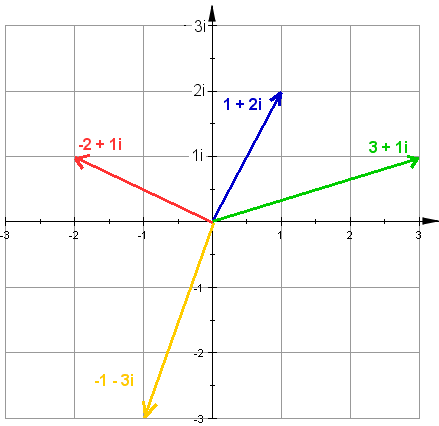
Für die 4 Grundrechenarten mit komplexen Zahlen gelten nun die altbekannten Rechengesetze, insbesondere das Distributivgesetz:
Beispiel:
(2-5i).(-4+3i)
= 2.(-4)+2.3i-5i.(-4)-5i.3i
= -8 + 6i + 20 i - 15.i2
= -8 + 26i - 15.(-1)
= 23 + 26i
Für die geometrische Darstellung der Rechenarten wird Zeigerdarstellung benutzt. Auch die Darstellung komplexer Zahlen in Polarform ist möglich:
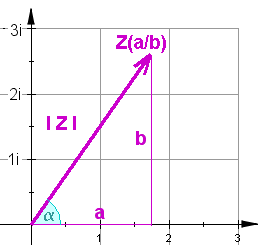
Real- und Imaginärteil der komplexen Zahl Z können mit Winkel und Betrag angegeben werden:
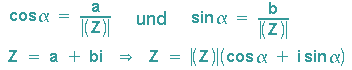
Dabei gilt:
Addition / Subtraktion komplexer Zahlen in Zeigerdarstellung:
Die Addition komplexer Zahlen entspricht in Zeigerdarstellung der Vektoraddition:
Multiplikation komplexer Zahlen in Zeigerdarstellung:
Multipliziert man reelle Zahlen am Zahlenstrahl, dann wird die eine um den Betrag der anderen Zahl gestreckt, bei Multiplikation mit einer negativen Zahl kommt zusätzlich noch eine Drehung um 180° hinzu.
Ebenso entspricht auch die Zeigermultiplikation komplexer Zahlen einer Drehstreckung:
z2 wird gestreckt, Streckfaktor ist der Betrag von z1. Zusätzlich wird z2 noch um den Winkel gedreht, den z1 mit der x-Achse bildet.
Siehe auch "affine Abbildungen"!
Mit Hilfe des Distributivgesetzes kann die Voreinstellung (2+i)(3-i)=7+i überprüft werden.
Division komplexer Zahlen (algebraisch)
Es sei z1= a + bi und z2 = c + di.
Wir suchen also den Bruch
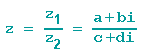
Wer will schon die imaginäre Zahl i im Nenner eines Bruches? Wir benutzen also die 3. binomische Formel zum Erweitern und multiplizieren aus:
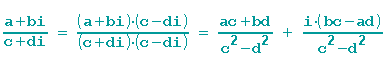
Konjugiert komplexe Zahlen
Sei z = a + bi, dann heißt 
die zu z konjugiert komplexe Zahl. In der Gaußchen Zahlenebene erhält man sie durch Spiegelung des Zeigers z an der reellen Zahlenachse.
Für das Produkt einer komplexen mit ihrer konjugiert komplexen Zahl gilt:
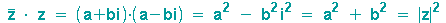
(Satz des Pythagoras)
Darstellung einer konjugiert komplexen Zahl in Polarkoordinaten:
Wegen
gilt
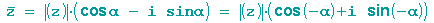
Bei der Multiplikation in Polarform werden die beiden Beträge multipliziert, die jeweiligen Winkel werden addiert: (Formel mit Distributivgesetz und Additionstheoremen für sin und cos herleitbar )
Bemerkung zu einer eventuellen Erweiterung der komplexen Zahlen
Da die Zahl i ja 'erfunden' wurde, um Gleichungen lösen zu können, die auf x2 = -1 führen, könnte man sich ja die Frage stellen, ob man für x2 = i eine neue 'superkomplexe' Zahl benötigt, mit der dann die Wurzel aus i bezeichnet wird. Denken wir das doch mal durch:
Gesucht ist z mit z2 = i .
Also quadrieren wir z:
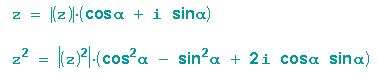
Der Betrag unserer gesuchten Zahl z muss 1 sein (nur 12=1), sie ist natürlich rein imaginär, somit ist der reelle Teil Null
und der Betrag 1 kann nur aus dem imaginären Teil resultieren, es gilt also
Schon haben wir ein Gleichungssystem mit 2 Unbekannten, das wir lösen können: Wir lösen die 2. Gleichung nach dem Sinus auf und setzen das Ergebnis in die 1. Gleichung ein:
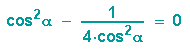
Dies führt zu den Lösungen
und wir erhalten
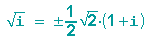
| © 2011 Asti | Links für Unterricht | PoVRay-Site |