Matrix
Wir betrachten die Vektorabbildung
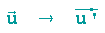
für die gelten soll (ui und ui' sind dabei die Komponenten der beiden Vektoren):
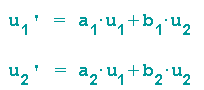
Dafür wird eine abkürzende Schreibweise benutzt:

Das Zahlenschema
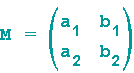
wird dann Matrix genannt (selbstverständlich gibt es nicht nur (2,2)-Matrizen, aber da wir beim Thema 'Möbiustransformation' dauernd komplexe Zahlen benutzen, werden hier nur solche Beispiele vorgestellt).
Einfache Beispiele:
Beispiel 1: Streckung um den Faktor s
Hierzu gehört die Matrix

denn
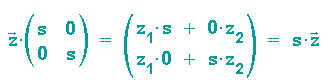
Beispiel 2: Rotation einer komplexen Zahl um den Winkel ß
-
Einschub Additionstheoreme Sinus und Kosinus:
Für die Addition zweier Winkel x und y gilt:
sin (x+y) = sin x cos y + cos x sin y
cos (x+y) = cos x cos y - sin x sin y
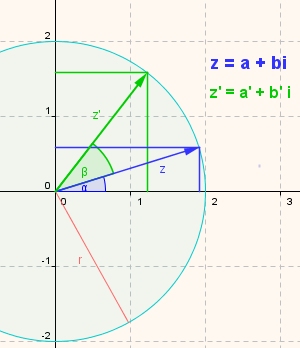
Für Realteil und Imaginärteil der komplexen Zahlen z und z' gilt:

Die zweite Zeile wird mit Hilfe des Additionstheorems umgeformt, die erste Zeile wird dann in die zweite Zeile eingesetzt. Man erhält:
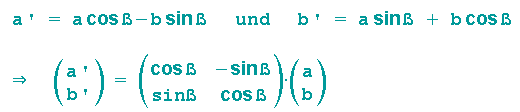
Beispiel 3: Die komplexe Zahl z=1+0i wird durch eine Drehstreckung in die komplexe Zahl z'=a+bi überführt.
also
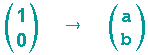
dann gehört dazu die (2,2)-Matrix
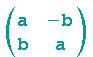
denn
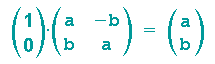
Ist ja schön und gut, aber warum denn ein -b??? Durch die Multiplikation mit 0 fällt es ja eh weg. Also ein genaueres Hinsehen ist angesagt:
Die Matrix für die Drehung ist bereis bekannt, nämlich:
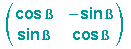
Auch die Matrix für Streckung kennen wir, für den Streckfaktor s gilt:
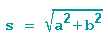
Also führen wir nun beide Abbildungen hintereinander aus:
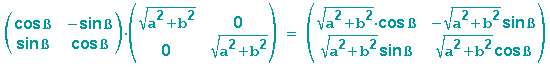
Mit

erhalten wir
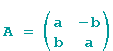
und das Geheimnis um -b ist gelöst.
Rechengesetze für Matrizen kann man dann in einem geeigneten Mathebuch nachlesen, oder auch im Netz aller Netze.
Inversion einer Matrix
Auch hier wieder die Beschränkung auf (2,2)-Matrizen, da dies ja das vergessene Vorwissen zum Thema 'Möbiustransformation' mit komplexen Zahlen ist.
-
Einschub Determinante:
Als abkürzende Schreibweise für die Differenz zweier Produkte kann man eine (2,2)-Determinante verwenden:
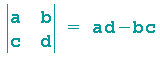
Wenn ad-bc von Null verschieden ist (die zugehörige Matrix wird in diesem Fall regulär genannt), dann definiert man die zu
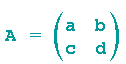
inverse Matrix A* als die zur inversen Abbildung gehörende Matrix.
... und weil dies weder anschaulich ist noch verständlich klingt, gibt's nun ein Beispiel.
Eine affine Abbildung sei durch die folgenden Abbildungsgleichungen gegeben:

Wir suchen nun die inverse Abbildung, d. h. diejenige Abbildung, die dies wieder rückgängig macht, also x' und y' wieder auf x bzw. y abbildet.
Wir müssen also unser Gleichungssystem nach x und y auflösen:
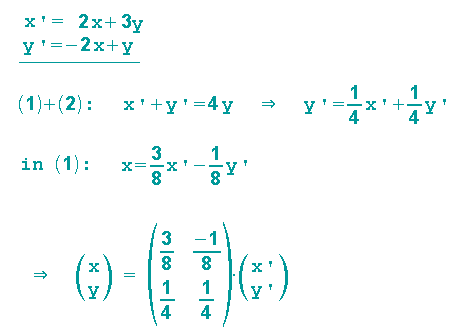
Wir haben also die inverse Matrix A* gefunden!
Da das Produkt von A mit A* der Hintereinanderausführung der beiden entsprechenden Abbildungen entspricht, folgen wir der Devise "Vertrauen ist gut, aber Kontrolle ist besser" und überprüfen unser Ergebnis am Beispiel der komplexen Zahl z=a+bi.
Zunächst wenden wir die ursprüngliche Abbildung A auf z an, um z' zu erhalten:
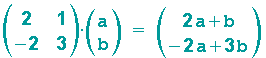
Nun wenden wir die Umkehrabbildung auf z' an (und hoffen schon mal, dass wir auch wieder z erhalten):
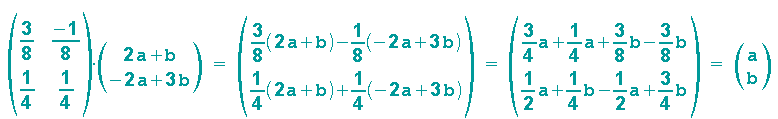
So soll es sein!!! ... und wir erkennen auch noch, dass die Multiplikation von Matrix mit inverser Matrix die Einheitsmatrix ergibt:
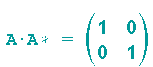
Hätten wir die inverse Matrix auf diese Weise definiert, wer hätte sie dann zu einem geg. Beispiel ausrechnen können?
Unser Beispiel hilft uns nun, für eine (2,2)-Matrix eine Formel für das Berechnen der inversen Matrix zu finden: Wir lösen unser Gleichungssystem eben mit den Koeffizienten a,b,c und d.
Um etwas Schreibarbeit zu sparen, bezeichnen wir die zug. Determinante mit det:
det = ad - bc
Zur Abbildung schreiben wir das Gleichungssystem auf:
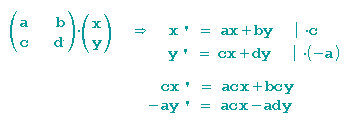
und lösen es nach geeigneter Multiplikation und anschließender Addition der beiden Gleichungen nach y auf:
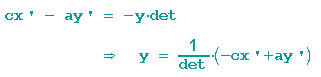
Das Ergebnis wird in die erste Gleichung eingesetzt und dann nach x aufgelöst.
An den beiden Lösungen für x und y können wir dann die inverse Matrix A* ablesen:
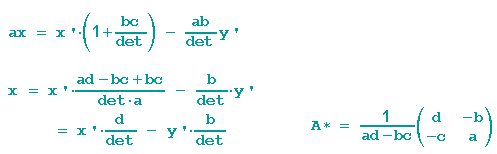
... und wer nun ein paar eigene Beispiele berechnen will, kann sein Ergebnis hier überprüfen!
Und wer's genauer wissen will und sich mit Eigenvektoren, Rechengesetzen, Gruppen, (n,n)-Matrizen und Ähnlichem vergnügen will, der schlage ein Mathebuch auf! Hier geht's nun zurück zur inversen Möbiustransformation.
| © 2009/10 Asti | Links für Unterricht | PoVRay-Site |