Kegelschnitte

Die Menge aller Punkte, deren Abstand von einem Brennpunkt F das n-fache des Abstandes zu einer fixen Geraden g ist, ergibt eine Parabel für n=1.
Die Menge aller Punkte, deren Abstand von einem Brennpunkt F das n-fache des Abstandes zu einer fixen Geraden g ist, ergibt eine Ellipse für n<1.
Die Menge aller Punkte, deren Abstand von einem Brennpunkt F das n-fache des Abstandes zu einer fixen Geraden g ist, ergibt eine Hyperbel für n>1.

Die Parabel

Im folgenden Beispiel: Parabel mit Brennpunkt F und fixer Gerade g. Die Strecken PQ und PF sind gleichlang. Ziehe mit der Maus den Punkt Q auf der Geraden g und beobachte, auf welcher Linie sich der Punkt P bewegt.

Erläuterung zur Konstruktion: Für alle Parabelpunkte P _n soll der Abstand von Q_n zu F gleich dem Abstand von P_n zu F sein, d. h. P_n liegt immer auf der Mittelsenkrechten der Verbindung Q_nF und gleichzeitig senkrecht über Q_n.

Alle 3 Kegelschnitte gemeinsam: Ziehe wieder mit der Maus den Punkt Q.

Im Folgenden noch 2 Animationen und einige Links im Internet zum Thema "Kegelschnitt":



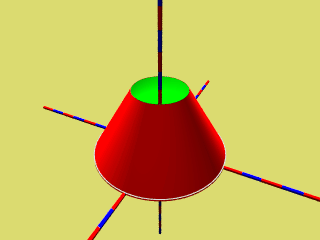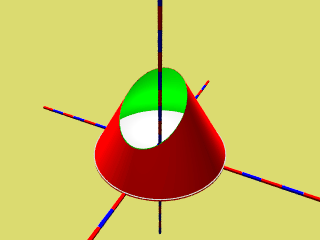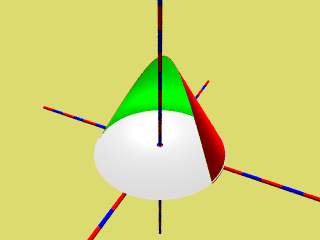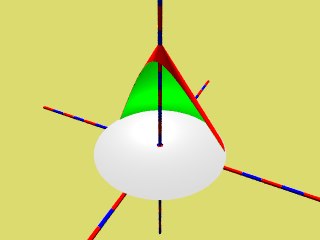
Dreht man die schneidende Ebene geeiget, so erkennt man nacheinander Kreis, Ellipse, Parabel und Hyperbel als Schnittkante des Kegels.

Ebenso kann man die Kegelschnitte Parabel, Ellipse und Hyperbel als Zentralprojektion eines Kreises auf eine zur Kreisebene nicht parallele Ebene erhalten:



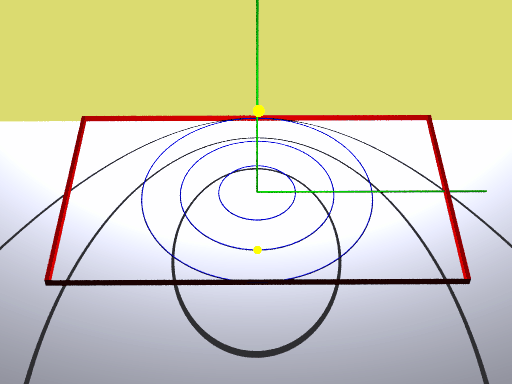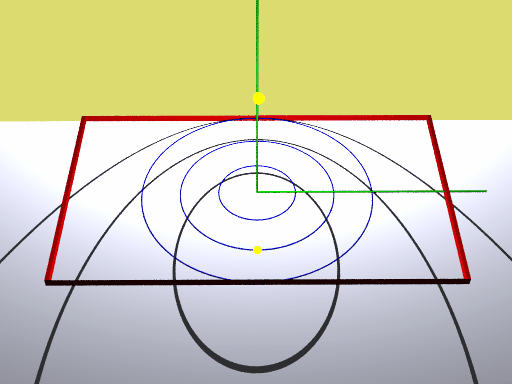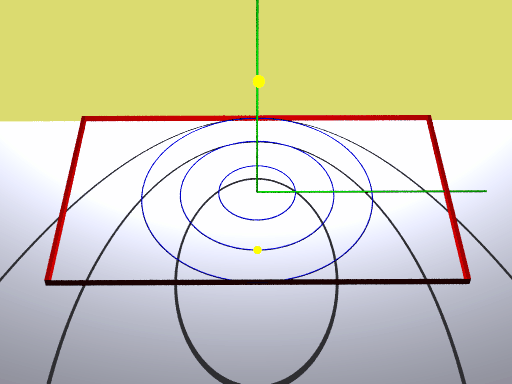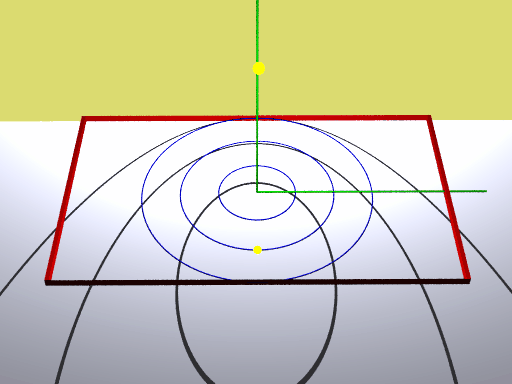
In der obigen Animation gibt die untere gelbe Kugel die Projektion der Lichtquelle auf die xz-Ebene an, die obere gelbe Kugel stellt die Lichtquelle dar. Die Kreise liegen in der xz-Ebene und werden auf die yz-Ebene projiziert. Die Kreisradien betragen eine, zwei und drei Längeneinheiten.

Man erkennt:
Ist der Kreisradius kleiner als der Abstand der LQ vom Koordinatenursprung, so erhält man als Zentralprojektion des Kreises eine Ellipse.
Ist der Kreisradius gleich dem Abstand der LQ vom Koordinatenursprung, so erhält man als Zentralprojektion des Kreises eine Parabel.
Ist der Kreisradius größer als der Abstand der LQ vom Koordinatenursprung, so erhält man als Zentralprojektion des Kreises eine Hyperbel.

Links im Internet:

Eim Überblick über die Kegelschnitte und die zugehörigen Gleichungen.
Interaktives JAVA-Applet zur Demonstration von Kegelschnitten
Verschiedene Kegelschnittkontruktionen
Kegelschnitte als Ortskurven mit DYNAGEO (Euklid)

• Zum Seitenanfang