Fläche von Quadrat und Rechteck
Für die Fläche eines Quadrates gilt: A = a2.
Dabei ist a die Seitenlänge des Quadrates.
Für die Fläche eines Rechteckes gilt: A = a b.
Dabei sind a und b die Seitenlängen des Rechteckes.
Quadratwurzel
Die Quadratwurzel aus einer nichtnegativen Zahl a ist diejenige nichtnegative Zahl, die mit sich selbst multipliziert wieder a ergibt.

Zusammenhänge der trig. Funktionen
Hier verwendet:
sin ß : cos ß = tan ß
cos ß : sin ß = cot ß
cot ß = 1 : tan ß
Diese Beziehungen ergeben sich direkt aus der Definition von Sinus, Kosinus, Tangens und Kotangens.
Mittelwert
Der Mittelwert (Durchschnittswert) von zwei oder mehr Zahlen ist der "in ihrer Mitte liegende" Wert:
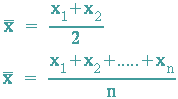
Ableitung
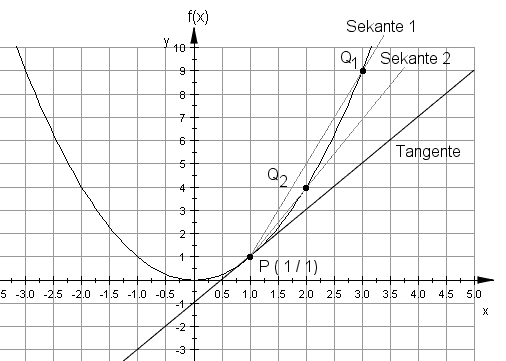
Sucht man die Steigung einer nichtlinearen Funktion in einem Punkt P, so wählt man zunächst die Sekante durch die Punkte Q1 und P, läßt dann den Punkt Q1 zu P wandern (Punkt Q2), bis er schließlich auf P trifft und die Sekante zur Tangente wird.
Die Steigung der Tangente im Punkt P wird dann als Steigung (Ableitung) an dieser Stelle bezeichnt.
Führt man dies für alle Punkte P auf dem Funktionsgraphen durch (sofern f(x) überall differenzierbar ist), so erhält man die Ableitungsfunktion:
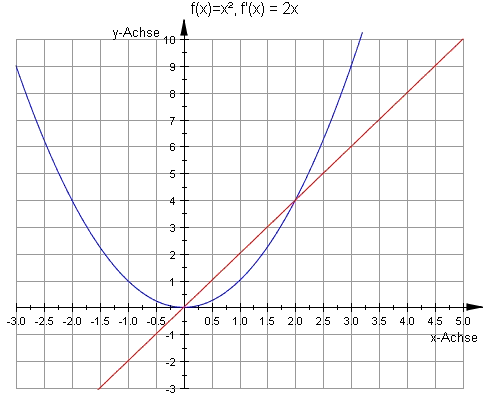
Von der ersten Ableitung f'(x) kann man dann auch die zweite Ableitung f''(x) bilden, die dann die Steigung von f'(x) angibt, uund so weiter, Differenzierbarbkeit sei jeweils vorausgesetzt:
|
|
... und wer noch ein bisschen üben will und seinem Mathelehrer eine Zusatzkorrektur verschaffen will, kann sich noch selbst am folgenden Ableitungspuzzle testen. In der ersten Zeile ist die Funktion f dargestellt, in Zeile 2 ihre 1. Ableitung f', in Zeile 3 ihre zweite Ableitung f''.
Drucke dir die Grafik aus und ergänze die leeren Felder. Achte dabei auf die Skalierung der Koordinatenachsen und zeichne so genau wie möglich.
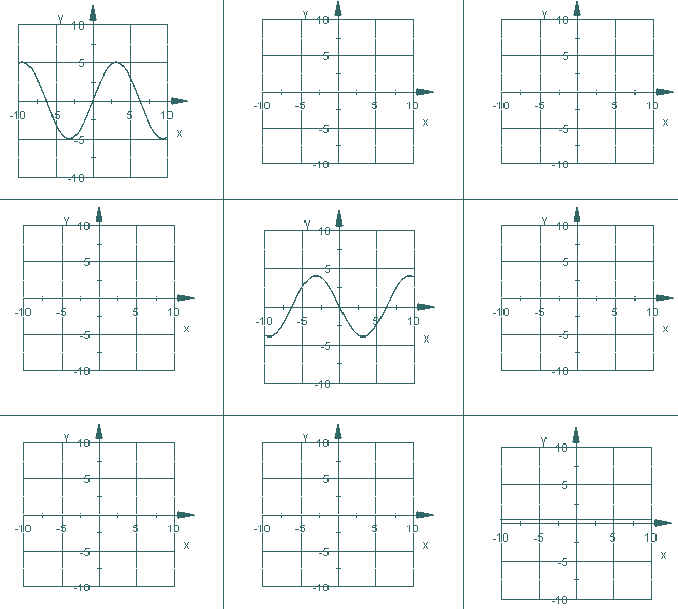
... und wer damit nicht klar kommt, kann hier Angebote zum Ausfüllen der leeren Felder finden, diese sind nicht in der richtigen Reihenfolge angegeben!!!
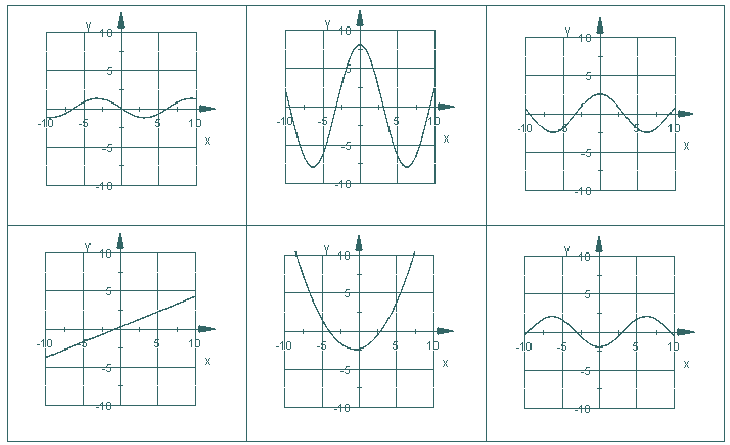
... noch ein zweites Ableitungspuzzle, diesmal jedoch ganz ohne Lösungsvorschläge:
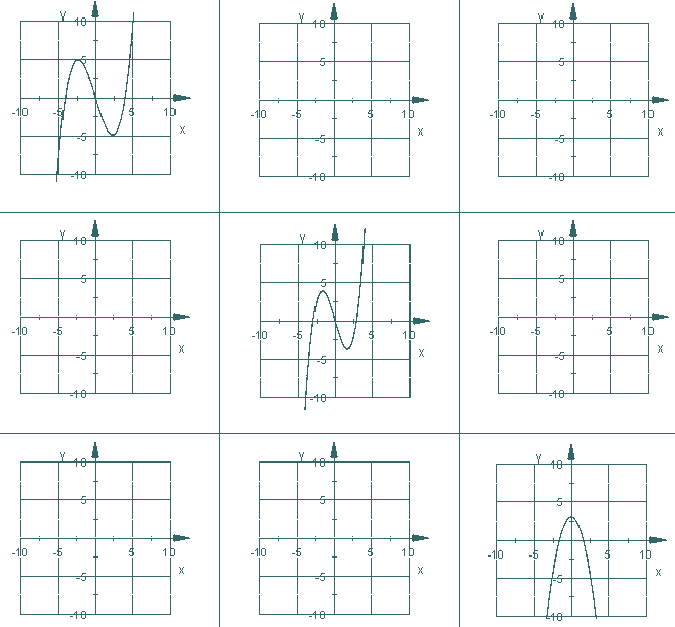
Geradengleichungen
| Hauptform | y = mx +b |
| 2-Punkte-Form | 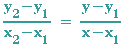 |
| Punkt-Steigungs-Form | 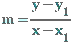 |
Distributivgesetz (Verteilungsgesetz)
Eine Summe wird mit einer Zahl multipliziert, indem man jeden Summanden mit der Zahl multipliziert und anschließend die Produkte addiert:
(a+b)c = ac + bc
Ebenso gilt:
(a-b)c = ac - bc
(a+b): c = a : c + b : c
(a-b): c = a : c - b : c
Konvergenz und Divergenz
Eine Folge von Zahlen hat möglicherweise die Eigenschaft, sich mit wachsender Anzahl der Folgeglieder einem Grenzwert (Limes) zu nähern. Sie wird dann konvergent genannt.
So hat z. B. die Folge
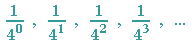
den Grenzwert 0. Existiert der Limes nicht, ist die Folge divergent wie z. B. die alternierende Folge -5, +5, -5, +5, ...
Newton'sches Verfahren und Konvergenz: Für die Nullstelle gilt
f(x) = 0,
was sich auch als Fixpunktgleichung darstellen läßt (Ein Wert x, der die Gleichung
f(x) = x
erfüllt, d.h. der durch die Anwendung der Funktion unverändert bleibt, heißt Fixpunkt):
g(x) = f(x) - 0 + x
Nach unterschiedlichen Fixpunktsätzen gibt es daher mehrere Ansätze zur Untersuchung der Konvergenz des Verfahrens.
Beispielsweise kann die lokale Konvexität, bzw. Konkavität untersucht werden: Ist f(x) zweimal differenzierbar und ist die 2. Ableitung in einer Umgebung der Nullstelle positiv, dann konvergiert die Newtonfolge für alle Startwerte im betreffenden Intervall, die größer als die Nullstelle sind, gegen die (größte) Nullstelle im Intervall.
Im Beispiel ist dies erfüllt:
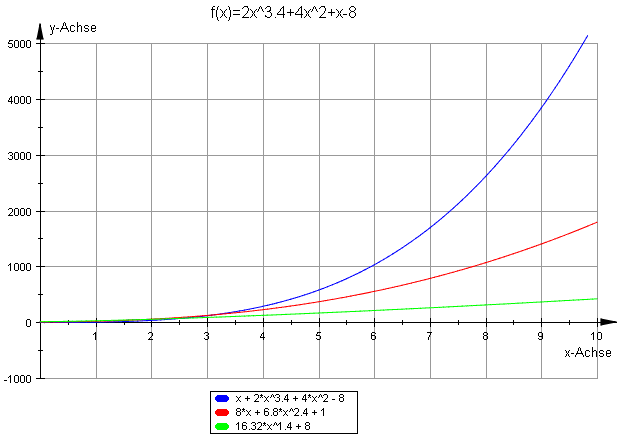
Für die Nullstellen der sinus-Funktion läßt sich jedoch kein solches Intervall finden: Die 2. Ableitung ist an den Nullstellen ebenfalls Null.
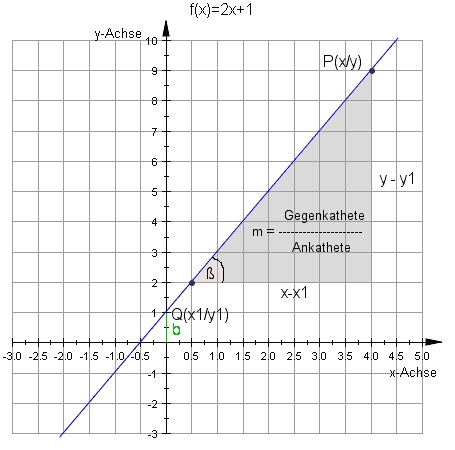
Tangente
Eine Gerade, die eine nichtlineare Funktion f(x) in (mindestens) einem Punkt berührt (nicht schneidet), heißt Tangente in diesem Punkt.
Rekursion
"Rekursion" stammt aus dem Lateinischen und bedeutet "Zurückführung". Ein Objekt ist dann rekursiv, wenn es Varianten von sich selbst enthält oder mit Hilfe von Varianten seiner selbst definiert ist (z.B. Geschichten innerhalb von Geschichten, Bilder innerhalb von Bildern, ...
Kreis
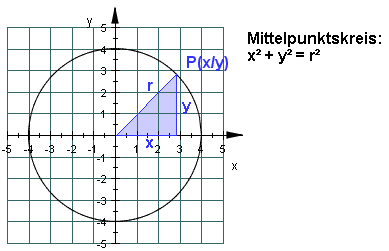
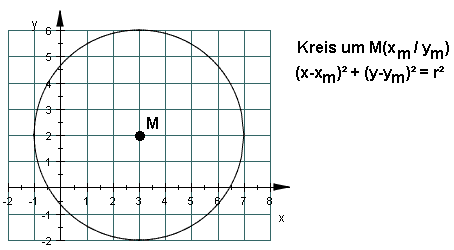
Für Flächeninhalt und Umfang eines Kreises mit dem Radius R gilt:
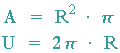
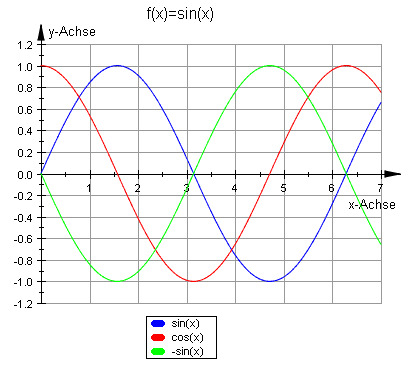
Sinus und Kosinus
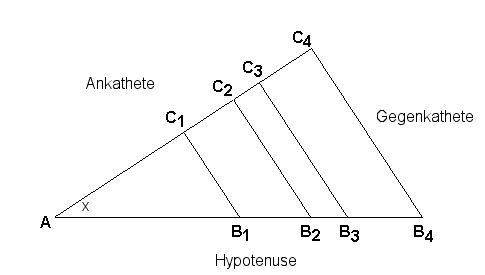
Im rechtwinkligen Dreieck wird sin(x) als das Verhältnis von Gegenkahete zu Hypotenuse definiert. Variiert man den Winkel x, so erhält man die Sinusfunktion:

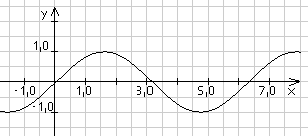
Entsprechend ist cos(x) das Verhältnis von Ankathete zu Hypotenuse:
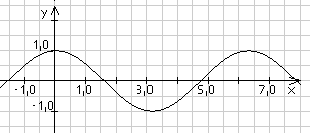
Winkelgeschwindigkeit 
Rotiert ein Körper mit konstanter Geschwindigkeit um eine feste Achse, dann rotieren alle seine Punkte mit ihm. Betrachtet man den Quotienten aus dem überstrichenen Winkel 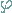 im Bogenmaß und der dazu benötigten Zeit, dann erhält man die Winkelgeschwindigkeit:
im Bogenmaß und der dazu benötigten Zeit, dann erhält man die Winkelgeschwindigkeit:
Bezeichnet man die Zeit für einen vollen Umlauf um den Winkel 360° = 2 mit T, dann gilt also:
mit T, dann gilt also:

Für die mittlere Winkelgeschwindigkeit gilt:
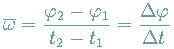
bzw.
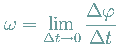
Dabei ist 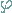 (im Bogenmaß) der dabei überstrichene Winkel.
(im Bogenmaß) der dabei überstrichene Winkel.
Für dem Momentanwert der Winkelgeschwindigkeit gilt dann:
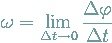
Bogenmaß
Für den Umfang eines Kreises gilt U = 2 r, was einem vollen Winkel von 360° entspricht. Wählt man den Radius r = 1 LE (Einheitskreis), dann entspricht 360° der Bogenlänge 2
r, was einem vollen Winkel von 360° entspricht. Wählt man den Radius r = 1 LE (Einheitskreis), dann entspricht 360° der Bogenlänge 2 . Man spricht nun von Bogenmaß. Für jeden Winkel
. Man spricht nun von Bogenmaß. Für jeden Winkel  kann man im Einheitskreis die zu ihm gehörende Kreisbogenlänge zuordnen und diese als Maßeinheit benutzen.
kann man im Einheitskreis die zu ihm gehörende Kreisbogenlänge zuordnen und diese als Maßeinheit benutzen.
Umrechnung Grad zu Bogenmaß am Besipiel  =25°:
=25°:
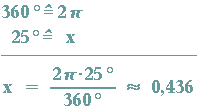
An der Formel erkennt man auch, dass nicht mehr die Einheit Grad, sondern eine unbenannte Zahl vorliegt.
Umrechnung Bogenmaß zu Grad am Besipiel x = 0,5 
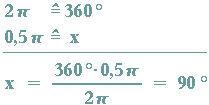
| © 2009-2024 Asti | PoVRay-Site |