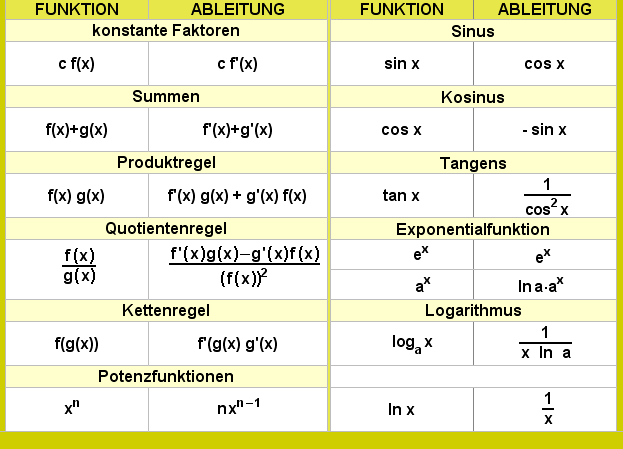
Differenzenquotient und Differentialquotient
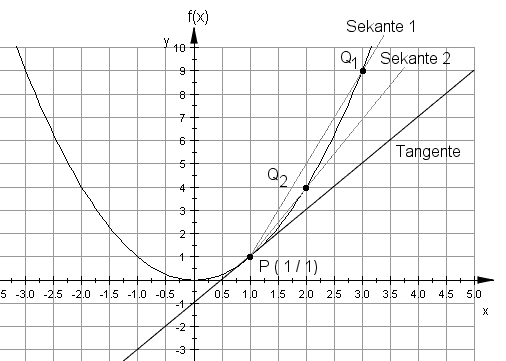
Sucht man die Ableitung einer differenzierbaren Funktion im Punkt P, so kann man zunächst die Steigung einer passenden Sekante (Gerade durch P und Q1, Gerade durch P und Q2,...) betrachten: Man erhält den Differenzenquotient.
Lässt man einen Punkt Q zum Punkt P hin wandern, so erhält man schließlich die Steigung der Tangente an die Funktion im Punkt P: Differentialquotient.
Bezeichnet man mit h die Differenz xQ - xP, so gilt:
Differenzenquotient:
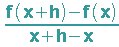
Differentialquotient:
Subtangente und Subnormale
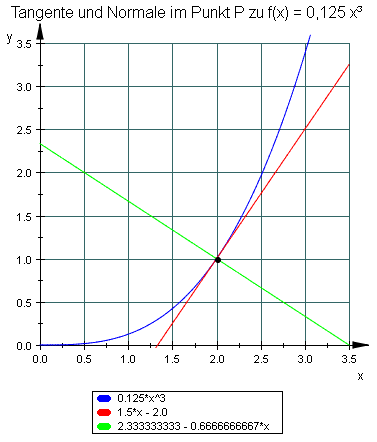
Projiziert man die Tangente im Punkt P einer differenzierbaren Funktion auf die x-Achse, so nennt man das Projektionsstück vom Schnittpunkt mit der x-Achse bis zum x-Wert des Berührpunktes P Subtangente:
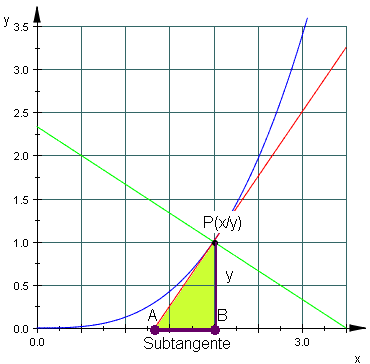
Für die Tangentensteigung gilt:
Ebenso erhält man die Subnormale als Projektion der Normalen auf die x-Achse als Strecke vom x-Wert des Berührpunktes P bis zum Schnittpunkt der Normalen mit der x-Achse:
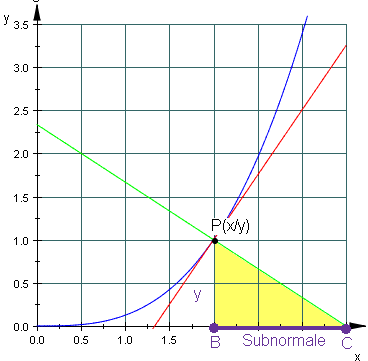
Für die Steigung der Subnormalen mn gilt:
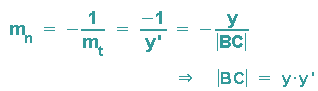
Ortsfaktor, Erdbeschleunigung
In Gegensatz zur Masse ist die Gewichtskraft FG vom Ort abhängig. An einem bestimmten Ort ist die Masse eines Körpers proportional zu dessen Gewichtskraft. Der Proportionalitätsfaktor heißt Ortsfaktor g. Er ist charakteristisch für den jeweiligen Orts. Andere Ortsfaktoren ergeben sich für Jupiter, Mond, Mars, ... im Vgl. zur Erde.
Aus der Gleichung FG=mg folgt, dass gilt:
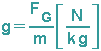
Aufgrund der Erdrotation und der daraus resultierenden Zentrifugalkraft ist der Ortfaktor an den Polen größer als am Äquator, als mittlerer Wert kann
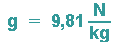
benutzt werden.
Ein frei fallender Körper (vernachlässigbar kleiner Luftwiderstand) fällt mit einer Beschleunigung, die vom Ort abhängt. Da
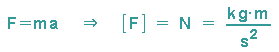
gilt, ergibt sich für g auch die Einheit einer Beschleunigung. g wird auch Erdbeschleunigung genannt:
Euklidische Geometrie
ist die Geometrie unseres Anschauungsraumes. Euklid von Alexandria (4. Jh. v. Chr.) fasste in Stocheia (Elemente der Mathematik) das damalige diesbezügliche Wissen zusammen. Noch bis zum Ende des 19. Jahrhunderts wurden Teile davon als Lehrbuch benutzt. In den "Elementen" wurde zum ersten Mal ein axiomatisch-deduktiver Aufbau der Mathematik gegeben: Grundbegriffe und -relationen werden aus der Wirklichkeit abstrahiert, weitere Aussagen müssen allein mit Hilfe logischer Schlussfolgerungen aus ihnen hergeleitet werden, ohne dass Anschauung zu Hilfe genommen werden darf. Erst um moderne physikalische Erkenntnisse (Relativitätstheorie, Gravitationstheorie) zu beschreiben, muss man zu allgemeineren Geometrien übergehen.
Als Beispiel für Euklids Axiomensystem hier die Inzidenzaxiome:
1. Zu zwei verschiedenen Punkten gibt es genau eine Verbindungsgerade.
2. Auf jeder Geraden liegen wenigstens 2 Punkte.
3. Es gibt wenigstens 3 Punkte, die nicht auf einer Geraden liegen.
Die Anordnungsaxiome befassen sich mit der Lage von Punkte auf Geraden.
Das Parallelenaxiom sagt aus, dass es zu einer Geraden g höchstens eine sie nicht schneidende zweite Gerade h gibt, die durch einen nicht auf g liegenden Punkt geht.
Die Kongruenzaxiome handeln von zueinander kongruenten Strecken.
Das Stetigkeitsaxiom (Archimedisches Axiom): Eine Strecke P0P1 wird n mal auf einer Halbgeraden abgetragen und erzeugt so die Punkte Pn und Pn+1 (entsprechende Strecken zueinander kongruent). Für einen Punkt dieser Halbgeraden gibt es eine nat. Zahl m, sodass dieser Punkt zwischen P0 und Pm liegt.
Hyperbolische Geometrie
Nur Euklids Parallelenaxiom wird wie folgt ersetzt: Liegt ein Punkt P nicht auf einer Geraden g, dann gibt es mindestens 2 Geraden, die die Gerade g nicht schneiden.
Anwendung findet sie in Differentialgeometrie, Topologie, Gruppentheorie, Dynamik, Zahlentheorie.
Zwei kleine Beispiele aus der Schulmathematik: Der Satz des Thales ist nun nicht mehr gültig. Weiterhin gilt jedoch: Haben 2 Höhen eines Dreiecks einen Schnittpunkt S, dann verläuft auch die dritte Höhe durch diesen Schnittpunkt.
Elliptische Geometrie
Zwei Geraden sollen immer einen Punkt gemeinsam haben. Ein Modell für die ebene elliptische Geometrie ist in der sphärischen Geometrie gegeben, wobei man als elliptische Ebene die Kugeloberfläche betrachtet. Die e-Geraden sind dann die Großkreise der Kugel, ein e-Punkt ist ein Paar sich diametral gegenüberliegender Kugelpunkte, womit klar wird, dass 2 e-Geraden immer einen gemeinsamen e-Punkt haben (2 Großkreise müssen sich ja immer in 2 diametralen Punkten schneiden).
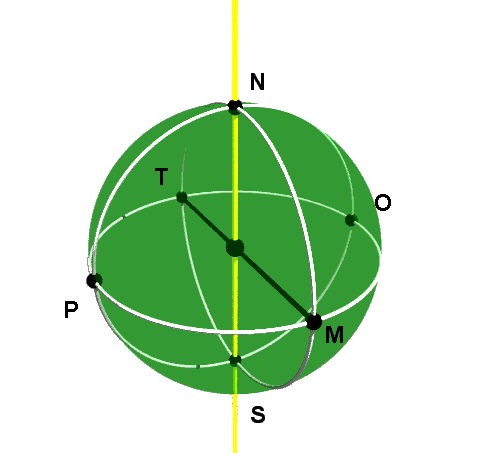
Die e-Punkte (N,S) und (M,T) bestimmen nun genau eine e-Gerade, nämlich die Gerade (NMST). Man kann jedoch vom e-Punkt (N,S) unendlich viele Lote auf die e-Gerade (MOTP) fällen.
Als Entfernung zweier e-Punkte kann man nun den kleineren Bogen des durch sie bestimmten Großkreises zwischen ihnen wählen. Die größtmögliche Entfernung in der elliptischen Geometrie ist dann 0,5*pi.
Die Winkelsumme in einem e-Dreieck ist immer größer als zwei Rechte.
Der Satz des Thales
Thales von Milet (ca 624 - 546 v. Chr., Vorsokratiker, Naturphilosph, Mathematiker, Astronom,... ) fand heraus, dass der Winkel an der Ecke C eines Dreieckes in einem Halbkreis über einer Strecke 90° beträgt. (Kurzformulierung: Die Winkel im Halbkreis sind rechte Winkel.) Auch die Umkehrung des Satzes ist gültig: Der Umkreismittelpunkt eines rechtwinkligen Dreiecks liegt in der Mitte seiner Hypotenuse.
|
|
Involution
... ist eine Abbildung, bei der Definitions- und Wertebereich identisch sind und die zu sich selbst invers ist (lat. involvere = einwickeln), d. h. der Bildpunkt des Bildpunktes ist wieder der Originalpunkt:
(P')' = P
Beispielsweise ist die Achsenspiegelung eine involutorische Abbildung, bei der jeder Punkt der Spiegelachse Fixpunkt ist.
Polarkoordinaten
... wurden 1691 von Bernouilli eingeführt: Ein Punkt ist charakterisierbar durch seinen Abstand von (0/0) und durch den Winkel, den seine Verbindungslinie zum Ursprung mit der x-Achse bildet.
Also lässt sich auch jede komplexe Zahl z = a+bi in Polarkoordinaten darstellen, d. h.
z = r (cos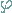
+ i sin) mit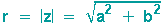 
.
Die Berechnung des Winkels 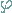hängt vom Quadranten ab, in dem z liegt.
Quadratische Ergänzung
... als Lösungsmethode für quadratische Gleichungen.
Gesucht seien die Nullstellen für y=x2-6x+8 .
Wenn anstelle der Zahl 8 eine 9 da stünde, dann könnten wir die 2. binomische Formel anwenden. Also addieren wir auf beiden Seiten der Gleichung die Zahl 1:
y+1=x2-6x+9=(x-3)2
.. und bringen die 1 auf der linken Seite wieder nach rechts:
y=x2-6x+9-1=(x-3)2 -1
Dies ergibt (zeichnerisch) eine Normalparabel, die um 3 Einheiten nach rechts und anschließend um 1 Einheit nach unten geschoben wurde:
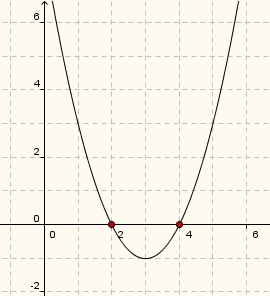
Die Nullstellen sind bereits ablesbar, können aber auch berechnet werden:
0=x2-6x+8
1=x2-6x+9
1=(x-3)2
1. Lösung: x1-3=+1, also x1=4
2. Lösung: x2-3=-1, also x2=2
Die Gleichung x2+bx+c=0 wird also so ergänzt, dass auf der linken Seite die erste oder zweite binomische Formel angewendet werden kann.
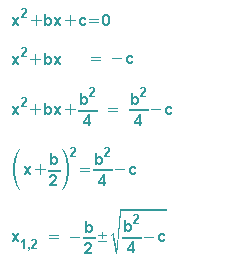
Man kann also auf diese Weise die p-q-Formel herleiten.
| © 2009-2024 Asti | PoVRay-Site |