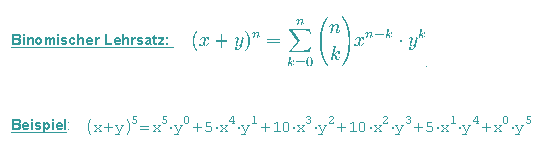Zufallsgröße

Eine Zuordnung



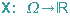
,die jedem Ergebnis eines Zufallsversuchs eine reelle Zahl zuordnet, wird Zufallsgröße (Zufallsvariable, stochastische Variable) genannt.

Hat X nur endlich viele oder abzählbar unendlich viele Werte mit positiver Wahrscheinlichkeit und liegen in jedem endlichen reellen Intervall nur endlich viele Werte, dann nennt man X und ihre Verteilung diskret.









































Erwartungswert

Eine Zufallsgröße X kann die Werte x1, x2, ..., xn annehmen. Die Zahl



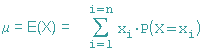
heißt Erwartungswert von X. Sie ist das gewichtete arithmetische Mittel der Elemente aus der Wertemenge von X.









































Varianz

Vorbemerkung: Statistische Maßzahlen

Mittelwert: Sind k=n Merkmalswerte x1, x2, ..., xn einer Stichprobe gegeben, so heißt



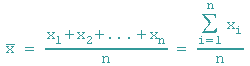
Mittelwert der Merkmalswerte.

Auch die relativen Häufigkeiten können zur Berechnung des Mittelwertes verwendet werden:




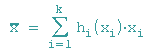
Der Zentralwert (Median) z der Merkmalswerte einer geordneten (rangierten) Stichprobe ist für ungeraden Stichprobenumfang der in der Mitte stehende Wert, für geraden Stichprobenumfang das arithmetische Mittel der beiden mittleren Werte.


Die Differenz zwischen dem größten und dem kleinsten Wert einer Stichprobe wird Spannweite s* oder Variationsweite s* genannt.


Als mittlere quadratische Abweichung s² oder empirische Varianz s² bezeichnet man das arithmetische Mittel der Abweichungsquadrate:(k=n)

Anmerkung:
s² wird v.a. in der "schließenden Statistik" (von einer Stichprobe werden Schlüsse auf die Gesamtheit gezogen) benutzt, die Formel (auch in manchen Taschenrechnern) hat oft den Nenner n -1 statt n.


Durch das Quadrieren der Abweichungen ändert sich die Maßeinheit, um dies zu verhindern wird wieder die Wurzel gezogen: Die Wurzel aus der mittleren quadr. Abweichung nennt man empirische Standardabweichung s.(k=n)


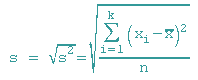
Bei der Durchführung eines Zufallsversuchs streuen die Werte, die eine Zufallsvariable X tatsächlich annimmt, um den Erwartungswert E(X). Um ihr Streuungsverhalten zu untersuchen, werden auch hier die Streuungsmaße aus der Statistik benutzt:
Die einzelnen quadr. Abweichungen werden anstatt mit der rel. Häufigkeit mit ihrer Wahrscheinlichkeit gewichtet: Die emprische Varianz wird zu


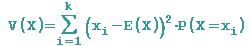
und wird als Varianz bezeichnet.












































Pascal'sches Dreieck

Das folgende Zahhlenschema wird Pascal'sches Dreieck genannt. Jede Zahl entsteht aus der Summe der über ihr stehenden Zahlen.






























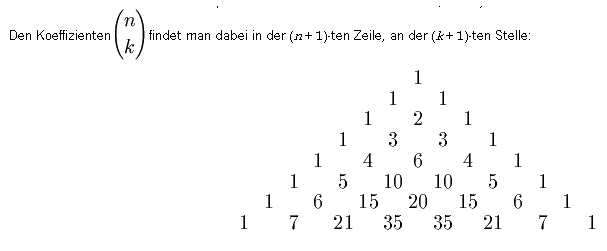
Der Binomische Lehrsatz




































Der Binomialkoeffizient

... ist eine abkürzende Schreibweise für



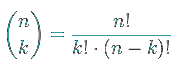
Das Ausrufungszeichen steht dabei für Fakultät.
























































Wahrscheinlichkeitsverteilung

Ordnet man jedem möglichen Wert xi, den die Zufallsgröße X annehmen kann, die Wahrscheinlichkeit P(X=xi) zu, dann nennt man dies die Wahrscheinlichkeitsverteilung der Zufallsgröße X. Die Wahrscheinlichkeitsverteilung kann graphisch dargestellt werden.
























































Verteilungsfunktion

Betrachtet man zu einer gegebenen reellen Zahl x die Wahrscheinlichkeit 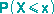, mit der die Zufallsvariable X einen Wert kleiner oder gleich x annimmt, dann erhält man eine Funktion Fx(x), die als Verteilungsfunktion bezeichnet wird.

Aus der Verteilungsfunktion lässt sich die Wahrscheinlichkeit einfach berechnen:

Sei E1 das Ereignis "X ist kleiner oder gleich a", sei E2 das Ereignis "a kleiner X und X kleiner gleich b".
Die beiden Ereignisse schließen dann einander aus, es ist dann


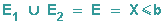
Also gilt



und
























































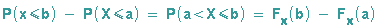
Wahrscheinlichkeitsfunktion

Eine Zufallsgröße X soll die folgenden Wahrscheinlichkeiten haben: P(X=xi)=pi

Dann heißt

Wahrscheinlichkeitsfunktion der betreffenden Zufallsgröße X.

Die Summe aller fx(xi) muss dann 1 ergeben, da X ja immer einen Wert annimmt. Für diskrete Zufallsvariable X ist also die Wahrscheinlichkeit für a kleiner X und X kleiner gleich b für beliebige Intervalle einfach berechenbar:






































































































































































































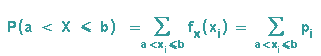
Exponentialfunktionen, die Eulersche Zahl e und der natürliche Logarithmus

Die Reserven in einer Kupfermine sinken jährlich um die Hälfte, der qm-Preis eines Grundstückes steigt jährlich auf das 1,5-fache, die Höhe einer Zimmerpflanze verdreifacht sich während der ersten 4 Jahre jährlich,.... Diese und ähnliche Sachverhalte führen bei graphischer Darstellung auf Funktionen der Form f(x) = k ax + c .

Erweitert man den Potenzbegriff derart, dass als Hochzahl beliebige reelle Zahlen erlaubt sind, und betrachtet man die Hochzahl als variabel, dann liegt eine Exponentialfunktion vor. Exponentielles Wachstum (ein Beispiel für eine Bakterienkultur findet Ihr hier), radioaktiver Zerfall (hier wieder ein Beispiel),... sind Beispiele für ihre Verwendung.

Das ff. Applet zeigt f(x)= ax, die Basis a ist am Schieberegler einstellbar.

Nur für a>0 und a ungleich 1 erhält man sinnvolle Ergebnisse.


Mit Hilfe des Schiebereglers sind nun die Monotonieeigenschaften in Abhängigkeit von der Basis a erkennbar. Auch wird ersichtlich, dass für a=1 kein exponentielles Wachstum (Zerfall) mehr vorliegt.

Die Ableitung der Exponentialfunktion

Bildet man den Limes, wendet das passende Potenzgesetz an und klammert ax aus, dann erhält man ff. Ergebnis:



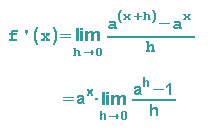
Sehen wir uns mal an, wie die Ableitung an der Stelle x=0 aussieht:



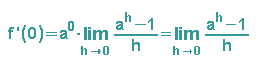
Man sieht also, dass bei der Berechnung der Ableitung einer Exponentialfunktion ax die Steigung an der Stelle x=0 eine Rolle spielt. An der vorherigen Formel sehen wir, dass dieser Limes an allen Stellen x auftaucht, er wird natürlicher Logarithmus von a genannt und mit ln a bezeichnet.



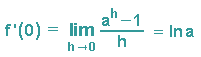
Insgesamt haben wir also folgendes Ergebnis erhalten:



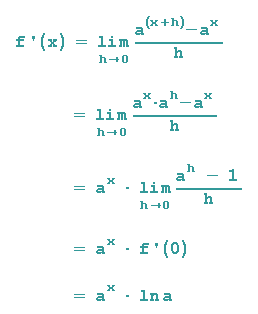
Da bei Exponentialfunktionen die Steigung an der Stelle x=0 in der Ableitung
f'(x)= ax ln a = ax f'(0)
auftaucht, zeichnen wir bei x=0 die Tangente ein und stellen uns die Frage, für welche Basis a ihre Steigung den Wert 1 hat.
Mit dem Schieberegler im ff. Applet kannst Du das herausfinden: Jeweils an der Stelle x=1 kannst Du die Basis ablesen, indem Du senkrecht nach oben bis zum Graphen eine Linie ziehst.


Sehen wir uns das genauer an:


Unser Ergebnis:

Hat die Basis von f(x)=ax ungefähr den Wert a=2,71, dann hat die Tangente bei x=0 die Steigung 1. Diese Zahl wird Eulersche Zahl e (Leonhard Euler,1707 bis 1783, Schweizer Mathematiker) genannt.
Da die Tangente bei x=0 die Steigung a0 ln a = ln a hat, gilt ln e=1.


Weitere Informationen über e sind in gängigen Mathebüchern und auch bei Wikipedia zu finden.

Zum Abschluss des Themas noch e-Funktion und Logarithmus naturalis als Umkehrfunktionen:
Graphisch geht die Umkehrfunktion durch Spiegelung der Ausgangsfunktion an der Winkelhalbierenden des 1. Quadranten hervor, für jeden Punkt P(x/y) werden x und y miteinander vertauscht:

y=ex wird zu x=ey , was durch Logarithmieren nach y aufgelöst wird:

y ln e = ln x, d. h. y = ln x, da ln e = 1.































































Standardabweichung
Die empirische Standardabweichung



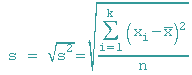
wird zu



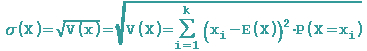
und wird als Standardabweichung bezeichnet.




















































































































































© 2010-2024 Asti PoVRay-Site