Singularitäten
Eine Kurve in einer Ebene kann eine Störung des glatten Verlaufs aufzeigen.
Solche Stellen werden Singularitäten genannt: Die Polstelle der ersten Funktion, die Spitze der zweiten Funktion, der zeitliche Verlauf eines Börsenkurses, ...
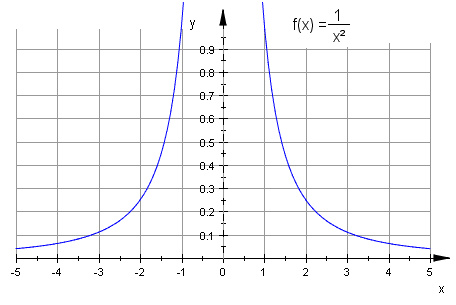
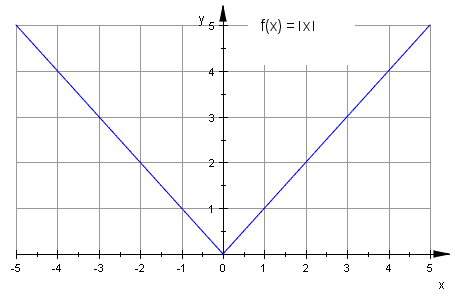
Auch 3-dimensionale Flächen können Singularitäten ("spitze Stellen") aufweisen. Eine sogenannte A1+- - Singularität hat der Doppelkegel: x2+y2-z2=0

Ändert man die Gleichung dieser Fläche nur geringefügig:
x2+y2-z2=a
und benutzt -0,5 < a < +0,5 , dann verschwindet die Singularität.
Die folgende Animation startet bei a = -0,5 und endet bei a = + 0,5. Nur bei a=0 ist die Singularität vorhanden.

Algebraische Flächen
Eine 2-dimensionale Fläche hat 2 Freiheitsgrade der Bewegung, d. h. zwei aufeinander senkrecht stehende Richtungen, derart, dass von einem Startpunkt aus jeder andere Punkt der Fläche erreicht werden kann, indem man sich ein Stück in der einen und in der anderen Richtung bewegt.
Auf der Erdoberfläche werden diese Richtungen durch die Längen- und Breitengrade vorgegeben.
Algebraische Flächen sind Lösungsmengen eines Polynoms mit 3 Variablen x, y und z und bestehen daher aus Zahlentripeln..
Beispiel 1: x + y + z = 1
Lösungen sind beispielsweise die Tripel (1/1/-1), (4/5/-8), (3/-2/0), .....
Beispiel 2: x2 + y2 + z2 + 1 = 0
hat keine reelle Lösung (die Summe dreier Quadratzahlen kann nicht -1 ergeben).
Beispiel 3: x2 + y2 + z2 = 0
hat die einzige reelle Lösung (0/0/0).
Beispiel 4: x2+ y2 = z
hat als Lösungsmenge ein Drehparaboloid: Wählt man P(x/y) frei in der Ebene und trägt darüber als Höhe x2 + y2 ab, dann stellt dies die Lösungsmenge dar.
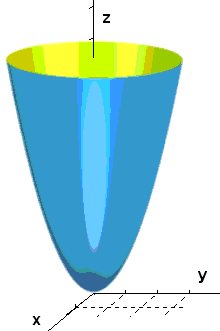
Man kann also auch sagen, x2+ y2 = z ist die Gleichung der abgebildeten Fläche.
Erweitert man auf den Zahlbereich der komplexen Zahlen, dann gehen keine Freiheitsgrade verloren.
Versucht man, die Gleichung
x2y3 + y2z3 + z2x3 = xyz
nach einer der drei Variablen aufzulösen, ist man schnell am Rand der Verzweiflung. Der Begriff "Lösen" muss neu präzisiert werden: Man spricht von der "Auflösung der Singularitäten algebraischer Varietäten" und unterscheidet zunächst zwischen glatten Flächen und solchen mit singulären Punkten.
Eine glatte Fläche ist z. B. eine Kugeloberfläche, eine mit singulären Punkten (Ecken und Kanten) ist eine Würfeloberfläche.
Beispiel 5: x2 - y2 = z2
hat die folgende Lösungsmenge:
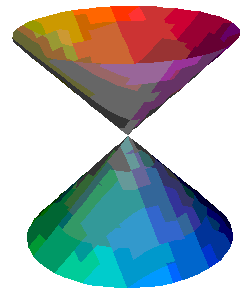
Software:
Viele Beispiele sind im Paket JavaView integriert:
Berechnung algebraischer Flächen mit der Software Singsurf
Eigenes Programmieren von 3D-Flächen mit PoVRay
Eine sehenswerte Galerie solcher Flächen bietet Tore Nordstrand .
Weitere Visualisierungen bietet das Programm SURFER, das für die Ausstellung IMAGINARY enwickelt wurde, präsentiert vom Mathematischen Forschungsinstitut Oberwolfach zum Jahr der Mathematik 2008. SURFER basiert auf der Software SURF
Quellenangaben für ein tieferes Einsteigen in das Thema:
Herwig Hauser: Die Auflösung von Singularitäten
Fakultät für Mathematik Universität Wien
www.hh.hauser.cc
herwig.hauser@univie.ac.at
Auflösungen von Singularitäten, oder: Wie bügele ich ein Tischtuch
Prof. Dr. Uwe Jannsen
Vortrag Universität Regensburg 03.04.2009
Wolfgang Wildgen: Das dynamische Paradigma in der Linguistik, 1987
Betrachtet man eine Ausgangskurve und deren Krümmungskreismittelpunkte, so entsteht die Evolute (lat: evolvere: entwickeln, deutlich machen, abspinnen, abwälzen) aus einer aufeinanderfolgenden Reihe von Krümmungskreismittelpunkten.
Krümmungskreise einer Parabel: Diejenigen Kreise, die sich bestmöglich an das Krümmungsverhalten der Parabel anpassen. Bei Bewegung des Punktes P auf der Parabel wird der zugehörige Krümmungskreis gezeigt.
|
|
Weitere Informationen zu Krümmungsradius und Krümmungskreismittelpunkt bei "Hüllkurven/Krümmung"!
Die Verbindungslinie von P zum Kreismittelpunkt M liegt jeweils auf der Normalen zur Parabel an der betreffenden Stelle. Zeichnet man also die Normalen, so kann man ebenfalls die Evolute als Hüllkurve (Enveloppe, Einhüllende) der Parabelnormalen erkennen:
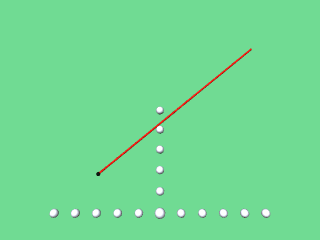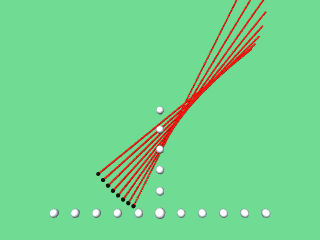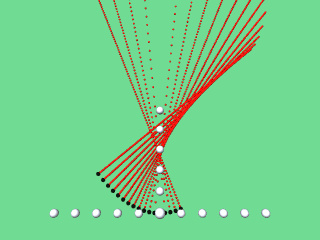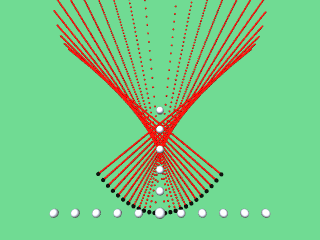 |
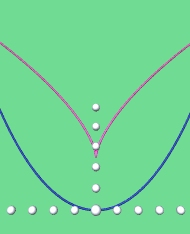 |
Zur Animation (f(x) = 0,2 x 2) noch die Evolute im Koordinatensystem mit beschrifteter Skala:
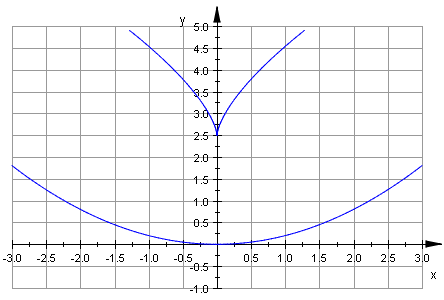
Krümmungskreise einer Ellipse:
Stelle zunächst mit gedrückter Maustaste an den Schiebereglern die Achsen a und b der Ellipse ein. Wähle dann im Menü "Ansicht auffrischen". Bewegen dann mit gedrückter Maustaste c.
Achtung: Bei Überschreitung der Grenzen verschwindet c, ist aber mit der Maustaste wieder holbar, ansonsten a vergrößern! A und B markieren die Grenzen des Schiebereglers c.
|
|
Bemerkungen:
- Die Evolute einer Ellipse wird ASTROIDE genannt.
- Für a=b erhält man einen Kreis und erkennt, dass dieser an jedem Punkt sein eigener Krümmungskreis ist. Als Evolute könnte man daher allenfalls seinen eigenen Mittelpunkt bezeichnen.
- Die Ellipse ist ihrerseits die Evolvente der Astroiden.
Eine Gerade ist nicht gekrümmt, ein Kreis hat eine konstante Krümmung, die jedoch mit wachsendem Radius kleiner wird. Bei einer beliebigen 2 mal differenzierbaren Funktion ändert sich die Krümmung von Punkt zu Punkt und wird daher mit Hilfe eines Kreises definiert, der sich im Berührpunkt möglichst gut an die Funktion "anschmiegt". Es macht Sinn, die Krümmung k als den Kehrwert des Radius' zu definieren:
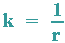
Es werden die folgenden Forderungen gestellt:
- Im Berührpunkt P(x0/y0) sollen Krümmungskreis und Funktion dieselbe Steigung haben.
- Der Kreismittelpunkt M(xm/ym) soll auf der Normale der Funktion liegen. Der Berührpunkt P liegt auf der Kreislinie.
- Die beiden zweiten Ableitungen sollen gleich sein.
Zunächst sammeln wir alle notwendigen Gleichungen und beginnen mit der Gleichung des Kreises und ihren beiden ersten Ableitungen (1. Ableitung: Kettenregel beachten, 2. Ableitung: Produktregel beachten):
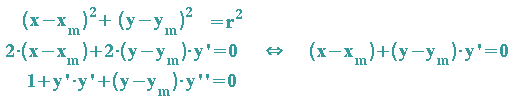
Tangente t(x) an die Funktion f(x) im Berührpunkt P:
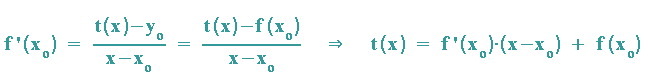
Normale n(x) zur Tangente:
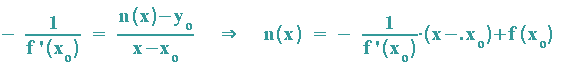
Als nächstes kümmern wir uns um die oben gestellten Forderungen:
A: P liegt auf der Kreislinie, wir setzen also die Koordinaten von P in die Kreisgleichung ein:
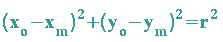
B: Der Krümmungskreismittelpunkt M liegt auf der Normalen im Berührpunkt P, seine Koordinaten werden also in die Normalengleichung eingesetzt:
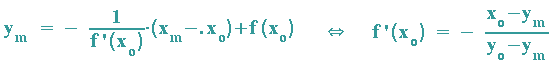
C: Im Berührpunkt P haben die ersten Ableitungen von Funktion und Krümmungskreis denselben Wert:
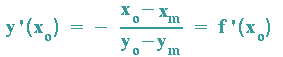
Man erkennt sofort, dass diese Gleichung zur Gleichung aus Forderung B identisch ist!
D: Im Berührpunkt P haben auch die zweiten Ableitungen von Funktion und Krümmungskreis denselben Wert: d. h. in der Gleichung 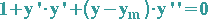 gilt:
gilt:

Also gilt:
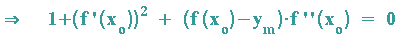
Wegen der Gleichheit von B und C haben wir nun 3 Gleichungen mit 3 Unbekannten xm, ym und r.
Nochmal im Überblick:
| (I) | 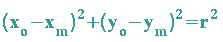 |
| (II) | 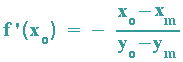 |
| (III) | 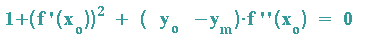 |
Skizzierte Möglichkeit, das Gleichungssystem zu lösen:
II und II werden nach y o - ym aufgelöst und beide Ergebnisse gleichgesetzt. Man erhält:
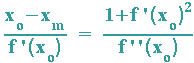
xo - xm = .... und yo - ym = .... werden beide in I eingesetzt und man erhält:
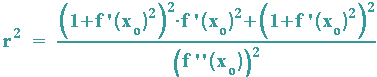
Mit Ausklammern und Wurzelziehen folgt:
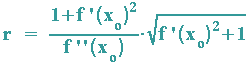
Für die Krümmung k erhält man dann den Kehrbruch dieses Wertes.
Nun können auch xm und ym berechnet werden:
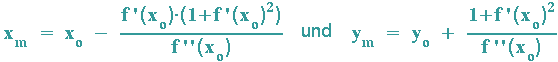
Quelle dazu im Internet: Prof. Dr. Dörte Haftendorn, Uni Lüneburg
Eine Seite mit ausgesprochen vielen mathematischen Themen in ausgesprochen unübersichtlicher Darstellung.
Das Huygenssche Prinzip
Ausgehend von verschiedenen Experimenten entwickelte Christiaan Huygens (1629 bis 1695) eine konstruktive Modellvorstellung, mit deren Hilfe das Verhalten von Wellen nach Hindernissen oder Öffnungen in einem Hindernis beschrieben werden kann, auch Reflexion und Brechung einer Welle werden hiermit beschreibbar.
Jeder Punkt einer fortschreitenden Wellenfläche wird als Ausgangspunkt einer neuen Kugelwelle, der sog. Huygensschen Elementarwelle, betrachtet, die nach FRESNEL in Richtung der alten Wellennormale ihre größte Amplitude hat und mit zunehmender Neigung gegen diese Richtung abnimmt.

Links im Internet:
Java Applet von Walter Fendt
Infos über Huygens aus Wikipedia
Versuche mit der Wellenwanne - Uni München
Applet zur Reflexion einer Welle für verschiedene Medien
Mechanische Wellen
Breitet sich eine mechanische Schwingung im Raum aus, so spricht man von einer mechanischen Welle.
Schwingungsfähige Teilchen, die kräftemäßig miteinander gekoppelt sind, müssen vorhanden sein, durch Energiezufuhr muss wenigstens ein Teilchen zu Schwingungen angeregt werden. Ohne Transport von Teilchen wird also Energie übertragen.
Sind Ausbreitungsrichtung der Welle und Schwingungsrichtung der einzelnen schwingenden Teilchen identisch, so liegt eine Longitudinalwelle vor (Beispiel: Schallwelle), stehen die beiden Richtungen senkrecht zueinander, so hat man eine Transversalwelle (Beispiel: Wasserwelle).
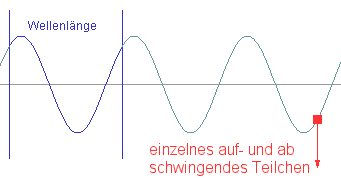
Die Ausbreitungsgeschwindigkeit einer mechanischen Welle ist das Produkt aus Wellenlänge und Schwingungsfrequenz.
Links im Internet:
Zusammenhang Schwingung-Welle und charakteristische Größen einer Welle (JAVA-Applet)
Wellenwanne und Interferenz von Wasserwellen
Download des Programmes "Wellenmaschine"
Darstellung von Longitudinal- und Transversalwelle (JAVA-Applet)
Materialseiten der Uni München zu mechanischen Wellen
Entstehung von Longitudinal- und Transversalwelle, 2 JAVA-Applets
| © 2009-2024 Asti | PoVRay-Site |