Herons Methode zur Bestimmung von Quadratwurzeln
Heron ging bei der Bestimmung einer Quadratwurzel von der folgenden Überlegung aus:
Ein Quadrat mit dem Flächeninhalt 16 cm2 hat eine Seitenlänge von 4 cm, was der Quadratwurzel des
Flächeninhaltes entspricht. Will man nun beispielsweise die Wurzel von 5 bestimmen, so braucht man ein Quadrat
mit dem Flächeninhalt von 5 cm2, die Seitenlänge liefert dann das gewünschte Ergebnis. Leider kann man
diese Seitenlänge graphisch nur sehr ungenau bestimmen.
Um ein genaues Ergebnis zu bestimmen, beginnt man mit einem Rechteck von 5 cm2 Flächeninhalt.
Die eine Seite wählt man z. B. x0 = 5 cm , die zweite Seite hat dann die Länge b = 1 cm.
x0 = 5 wird als erste Näherung für 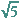 betrachtet, geradezu haarsträubend
schlecht, aber immerhin ein Anfang.
betrachtet, geradezu haarsträubend
schlecht, aber immerhin ein Anfang.
Für den nächsten Näherungswert x1 wählt man den Mittelwert der beiden Rechteckseiten. Der Mittelwert
von 5 und 1 ist 3, also x1 = 3 cm, die Seite b muss dann 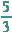 cm lang sein
und das Ganze sieht schon etwas "quadratischer" aus.
cm lang sein
und das Ganze sieht schon etwas "quadratischer" aus.
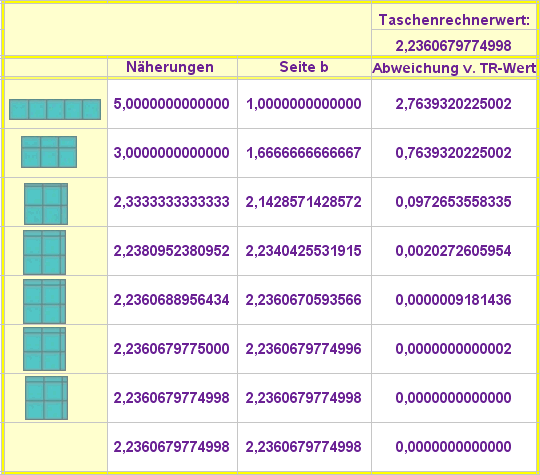
Im Folgenden sind mehrere Schritte dieses Verfahrens durchgeführt, die Näherung xiwird jeweils mit
dem Taschenrechnerwert von 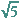 verglichen:
verglichen:
Man erkennt, dass x i schnell ein sehr genaues Ergebnis liefert.
Rekursionsformel für das Heron'sche Verfahren
Gesucht ist 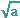 , man stelle sich also ein Rechteck mit dem Flächeninhalt a vor,
das in ein Quadrat mit demselben Flächeninhalt a und der Seitenlänge
, man stelle sich also ein Rechteck mit dem Flächeninhalt a vor,
das in ein Quadrat mit demselben Flächeninhalt a und der Seitenlänge 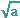 umgewandelt werden soll.
umgewandelt werden soll.
Die erste Näherung (Seite des ersten Rechtecks) sei x0, die zugehörige Seite b erhält man dann durch Division
des Flächeninhaltes a durch x0.
Es gilt also:
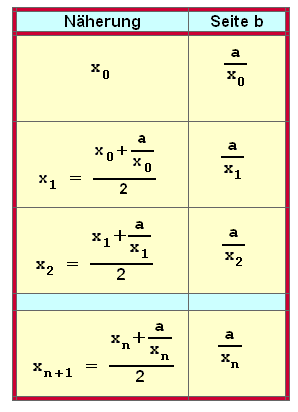
Die letzte Tabellenzeile liefert also die Rekursionsformel für Herons Verfahren zum Berechnen von Quadratwurzeln. Häufig wird sie in der folgenden Form dargestellt:
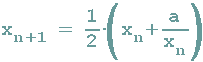
| © 2009 Asti | Links für Unterricht | PoVRay-Site |