Newton, Raphson und die näherungsweise Nullstellenbestimmung von Funktionen
Gesucht sind die Nullstellen einer Funktion f(x).
Am Beispiel der Funktion
f(x) = 2 x3,4 + 4 x2 + x - 8
erkennt man beim Zeichnen des Funktionsgraphen, dass der Schnittpunkt mit der x-Achse graphisch nicht genau abgelesen werden kann.
Als lineare Annäherung an die Funktion f(x) wird die Tangente t(x) im Punkt P(x0/f(x0) verwendet und mit der x-Achse geschnitten.
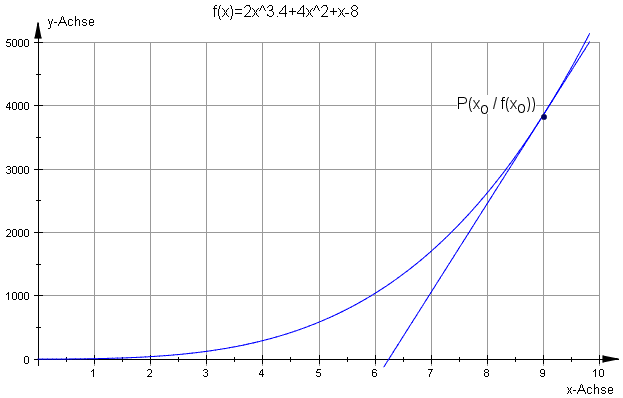
Der Punkt P(x0/f(x0) liegt also sowohl auf der Tangente als auch auf dem Funktionsgraphen.
Für die Tangentensteigung in P gilt: mt = f'(x0).
Nach der Punkt-Steigungs-Formel für Geradengleichungen gilt also:
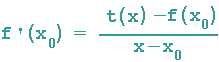
Diese Tangente schneidet die x-Achse im Punkt P1 (x1 / 0) =
( x1 / t(x1) , den man also in die Punkt-Steigungsformel der Tangentengleichung einsetzen darf:
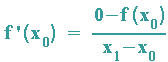
Diese Gleichung wird nun nach x1 aufgelöst:
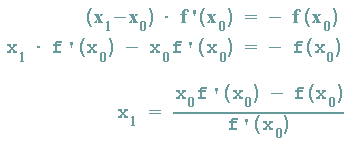
Nun betrachtet man die Tangente an f(x) am Schnittpunkt mit der x-Achse(x1 / 0) der ersten Tangente und wiederholt dieselben Überlegungen:
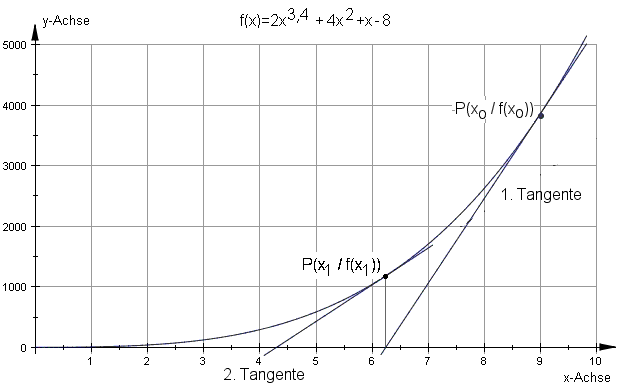
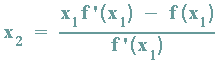
Im dritten Schritt wird nun die Tangente an f(x) an der Stelle x2 betrachtet, usw.
Ist man schließlich beim n-ten Schritt angelangt, erhält man also die folgende Formel:
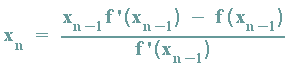
Häufig wird auch der (n+1)-te Schritt betrachtet:
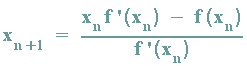
Unter Verwendung des Distributivgesetzes wird diese letzte Formel noch vereinfacht:
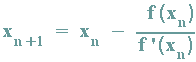
Da hierbei der Wert xn+1 mit Hilfe des vorherigen Wertes xn berechnet wird, (... ebenso auch xn mit Hilfe des vorherigen Wertes xn-1), wird eine solche Formel Rekusionsformel genannt.
Nullstellenberechnung der Funktion
f(x) = 2 x3,4 + 4 x2 + x - 8
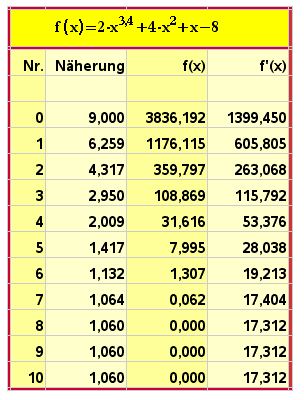
Bei diesem Beispiel konvergiert das Verfahren, ein Beispiel für Divergenz ist die Sinus-Funktion.
| © 2009 Asti | Links für Unterricht | PoVRay-Site |