Logarithmus
... ist nichts weiter als eine Hochzahl und dennoch bei den meisten Schüler/innen sehr unbeliebt.
Beispiel: 23=8, man nennt 3 den Logarithmus von 8 zur Basis 2. Und dazu gehört dann die folgende Schreibweise:

Zur Gleichung y = loga x gehört natürlich auch das Schaubild der Funktion:
Mit dem Schieberegler kannst Du bei gedrückter Maustaste die Basis a verändern.
Die Voreinstellung ist 23=8.
|
|
Willst Du das Schaubild einer Logarithmusfunktion mit Hilfe einer Wertetabelle zeichnen, dann gehst Du folgendermaßen vor:
y = log2x.
Um die Wertetabelle auszufüllen, stellst Du dir die Frage "2 hoch wieviel ergibt x?" Die Lösung trägst Du dann bei y ein. Sofort erkennst Du, dass negative Zahlen und die Zahl Null nicht das Ergebnis einer Zweierpotenz sein können: Der Definitionsbereich (die erlaubten Werte für x) der Logarithmusfunktion ist also die Menge der positiven reellen Zahlen. Da alle reellen Zahlen als Hochzahl für unsere positive Basis a benutzt werden dürfen, ist der Wertebereich (die Menge aller im Graph vorkommenden y-Werte) die Menge der reellen Zahlen.
Für x=1 gilt 20=1, also wird y=0 bei x=1 eingetragen.
Für x=2 gilt 21=2, also wird y=1 bei x=2 eingetragen.
Für x=3 gilt 2Kommazahl=3, also lassen wir den Tabellenplatz erst mal frei, suchen uns für x die Zweierpotenzen heraus und erhalten die ff. Wertetabelle (mit dem Applet kannst Du sie überprüfen):

Vertauscht man in der Funktionsgleichung x mit y, dann erhält man die Umkehrfunktion y = ax. Graphisch entspricht die Vertauschung von x mit y der Spiegelung eines Punktes Q(x/y) an der Winkelhalbierenden des ersten Quadranten.
Im ff. Applet sind Logarithmusfunktion und zugehörige Umkehrfunktion zu sehen. Wieder ist die Basis mit Hilfe des Schiebereglers veränderbar.
Für die Umkehrfunktion y = ax sind Definitions- und Wertebereich natürlich auch vertauscht.
|
|
Mit dem Schieberegler kannst Du nun verschiedene Werte für die Basis a einstellen und anhand der Funktionsgraphen die zugehörigen Monotonieeigenschaften in Abhängigkeit von a erkennen. Was stellst Du für a=1 fest?
Will man mit Logarithmen rechnen, dann braucht man auch einige
Logarithmengesetze.
Bildet man das Produkt aus zwei Potenzen gleicher Basis, wendet darauf das entsprechende Potenzgesetz an und logarithmiert dann das Ergebnis, dann erhält man:
Der Logarithmus eines Produktes ist gleich der Summe der einzelnen Logarithmen:
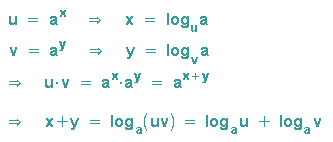
Mit den entsprechenden Potenzgesetzen sind auch die beiden nächsten Gesetze herleitbar:
Der Logarithmus eines Quotienten ist gleich der Differenz der einzelnen Logarithmen:
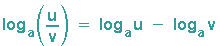
Der Logarithmus einer Potenz un ist gleich das n-fache des einzelnen Logarithmus:
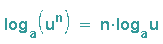
Viele Taschenrechner können nur mit dem Logarithmus zur Basis 10 (mit lg bezeichnet) und dem Logarithmus zur Basis e (mit ln bezeichnet) umgehen. Daher hier noch die zugehörige Umrechnung:
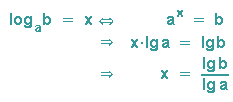
Anstelle von Zehnerlogarithmen kann zur Umrechnung natürlich auch der Logarithmus naturalis (ln) verwendet werden.
Exponentialfunktionen, die Eulersche Zahl e und der natürliche Logarithmus
Die Reserven in einer Kupfermine sinken jährlich um die Hälfte, der qm-Preis eines Grundstückes steigt jährlich auf das 1,5-fache, die Höhe einer Zimmerpflanze verdreifacht sich während der ersten 4 Jahre jährlich,.... Diese und ähnliche Sachverhalte führen bei graphischer Darstellung auf Funktionen der Form f(x) = k ax + c .
Erweitert man den Potenzbegriff derart, dass als Hochzahl beliebige reelle Zahlen erlaubt sind, und betrachtet man die Hochzahl als variabel, dann liegt eine Exponentialfunktion vor. Exponentielles Wachstum (ein Beispiel für eine Bakterienkultur findet Ihr hier), radioaktiver Zerfall (hier wieder ein Beispiel),... sind Beispiele für ihre Verwendung.
Das ff. Applet zeigt f(x)= ax, die Basis a ist am Schieberegler einstellbar.
Nur für a>0 und a ungleich 1 erhält man sinnvolle Ergebnisse.
|
|
Mit Hilfe des Schiebereglers sind nun die Monotonieeigenschaften in Abhängigkeit von der Basis a erkennbar. Auch wird ersichtlich, dass für a=1 kein exponentielles Wachstum (Zerfall) mehr vorliegt.
Die Ableitung der Exponentialfunktion
Bildet man den Limes, wendet das passende Potenzgesetz an und klammert ax aus, dann erhält man ff. Ergebnis:
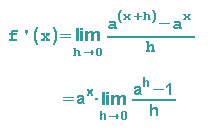
Sehen wir uns mal an, wie die Ableitung an der Stelle x=0 aussieht:
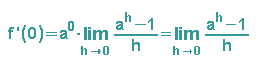
Man sieht also, dass bei der Berechnung der Ableitung einer Exponentialfunktion ax die Steigung an der Stelle x=0 eine Rolle spielt. An der vorherigen Formel sehen wir, dass dieser Limes an allen Stellen x auftaucht, er wird natürlicher Logarithmus von a genannt und mit ln a bezeichnet.
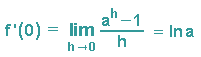
Insgesamt haben wir also folgendes Ergebnis erhalten:
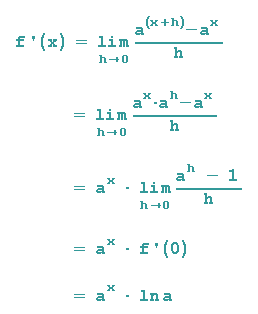
Da bei Exponentialfunktionen die Steigung an der Stelle x=0 in der Ableitung
f'(x)= ax ln a = ax f'(0)
auftaucht, zeichnen wir bei x=0 die Tangente ein und stellen uns die Frage, für welche Basis a ihre Steigung den Wert 1 hat.
Mit dem Schieberegler im ff. Applet kannst Du das herausfinden: Jeweils an der Stelle x=1 kannst Du die Basis ablesen, indem Du senkrecht nach oben bis zum Graphen eine Linie ziehst.
|
|
Sehen wir uns das genauer an:
|
|
Unser Ergebnis:
Hat die Basis von f(x)=ax ungefähr den Wert a=2,71, dann hat die Tangente bei x=0 die Steigung 1. Diese Zahl wird Eulersche Zahl e (Leonhard Euler,1707 bis 1783, Schweizer Mathematiker) genannt.
Da die Tangente bei x=0 die Steigung
a0 ln a = ln a hat, gilt ln e=1.
Weitere Informationen über e sind in gängigen Mathebüchern und auch bei Wikipedia zu finden.
Zum Abschluss des Themas noch e-Funktion und Logarithmus naturalis als Umkehrfunktionen:
Graphisch geht die Umkehrfunktion durch Spiegelung der Ausgangsfunktion an der Winkelhalbierenden des 1. Quadranten hervor, für jeden Punkt P(x/y) werden x und y miteinander vertauscht:
y=ex wird zu x=ey , was durch Logarithmieren nach y aufgelöst wird:
y ln e = ln x, d. h. y = ln x, da ln e = 1.
|
|
| © 2010 -2024 Asti | PoVRay-Site |