Möbiustransformationen: Symmetrien und Gruppen

Symmetrien aus dem Matheunterricht:

Beim Thema "Kurvendiskussion" in den Jahrgangsstufen 11 und 12 werden Funktionen / Relationen auf Achsensymmetrien zur x-Achse und y-Achse und auf Punktsymmetrie zum Koordinatenursprung hin untersucht.
f(x) ist zu einer zweiten Funktion g(x) symmetrisch zur x-Achse, wenn g(x) = - f(x) gilt. Es gilt:

Der Mathematiker Felix Klein (1849-1925) erweiterte den Symmetriebegriff. Bei Wikipedia könnt Ihr mehr über Felix Klein nachlesen.
Im Buch INDRA'S PEARLS von David Mumford, Caroline Series und David Wright wird im 1. Kapitel gut verständlich beschrieben, wie der erst 23-jährige Felix Klein bei seiner Berufung an die Universität Erlangen den Symmetriebegriff erweitert. Zitat aus o.g. Buch:
"... the study of the properties of the space which are invariant under a given group of transformations." (Drehungen, Verschiebungen, Spiegelungen, d.h. Transformationen, die ein 'Startobjekt' nicht verändern, ergeben seine Symmetriegruppe.)

Mit dem Begriff 'Gruppe' (siehe Schaltfläche am oberen Seitenrand) werden Regeln festgesetzt, die den sich wiederholenden Aspekt symmetrischer Muster wiedergeben.

Die 3 grundlegenden Symmetrien:


• Verschiebung eines Punktes (einer Punktmenge) der Ebene um a Einheiten nach rechts und um b Einheiten nach oben:
  T(x,y) = (x+a, y+b)
  T steht für Translation.


• Drehung gegen den Uhrzeigersinn um den Koordinatenursprung um einen Winkel ß:
  R(x,y) = (x cos ß - y sin ß , x sin ß + y cos ß)
  R steht für Rotation.


• Spiegelung an der y-Achse:
  S(x,y) = (-x,y)
  S steht für Spiegelung.

Während die Formeln für Verschiebung und Spiegelung unmittelbar einleuchten, ist die Formel für die Rotation nicht so leicht verständlich. Hier also ihre Herleitung:

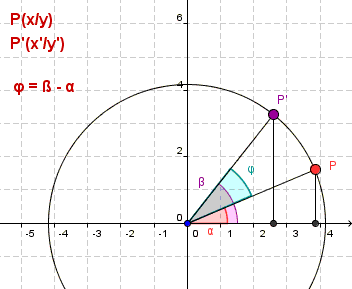
Es ist:



Nach den Additionstheoremen für trigonometrische Funktionen gilt dann:



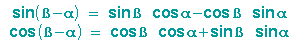
Einsetzen ergibt:



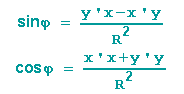
Wir haben nun ein Gleichungssystem mit den 2 Unbekannten x' und y':



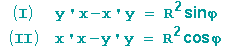
Wir setzten y' aus der 1. Gleichung in die 2. Gleichung ein:



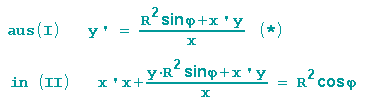
und erhalten



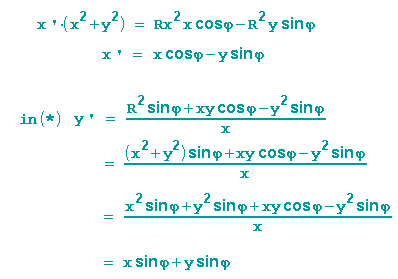
qed

Wenden wir uns nun den Gruppeneigenschaften (siehe Schaltfläche am oberen Seitenrand) zu:

Wir müssen die genannten Abbildungen miteinander verknüpfen, d.h. nacheinander ausführen, um zu sehen, ob die Verknüpfung tatsächlich wieder ein Gruppenelement (eine Symmetrie) ergibt, also eine Verschiebung, eine y-Achsenspiegelung oder eine Drehung gegen den Uhrzeigersinn um den Koordinatenursprung.

Im Buch Indra's Pearls gibt es viele Illustrationen mit Fliesenböden aus quadratischen oder sechseckigen Fliesen. Da ich PoVRay-Fan bin, zeige ich Beispiele, die mit dieser Freeware programmiert sind. Bei Mausklick auf die jeweilige Abbildung ist dann jeweils der Programmcode einsehbar. Die folgenden Beispiele erheben keinen Anspruch auf Vollständigkeit, d. h. die interessierten Leser/Innen müssen allgemein die Gruppeneigenschaften selbst überprüfen!

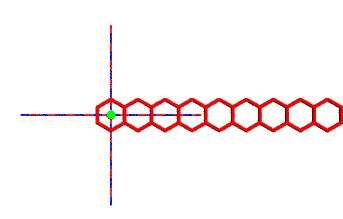
1. Mehrmalige Verschiebung einer Punktmenge A (Fliese o.ä.)
   Auf ein Sechseck mit Mittelpunkt im Ursprung wird die Verschiebung T(x,y)=(x+3,y) angewendet. Es ist unmittelbar zu erkennen, dass
   
   T² (x , y) = T (T (x , y)) = T (x+3 , y) = (x+6 , y)
   
   wieder eine Verschiebung und somit ein Gruppenelement ist:
   
   
   


2. Inverses und neutrales Element einer Symmetriegruppe:
   
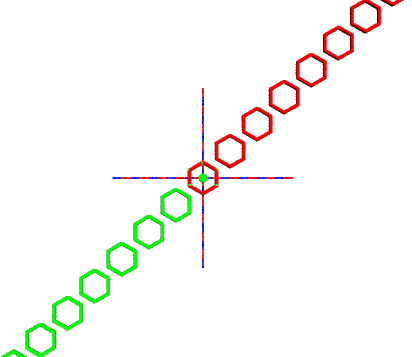
   Die Verschiebung
   
   T (x , y) = (x+3 , y+3)
   
   ist in der nächsten Abbildung dargestellt. Verschiebt man die Ausgangspunktmenge auch in die Gegenrichtung, hat man gleich das dazu inverse Gruppenelement T ^-1 .
   T ^-1 T = T T ^-1 = I (neutrales Element)
   T ^-1 = (x-3 , y-3)
   
   



3. Kombination zweier verschiedener Verschiebungen

Das Startsechseck wird schräg nach oben rechts und nach rechts waagrecht verschoben. Gleichzeitig werden die dazu inversen Verschiebungen dargestellt (Im Programmcode laufen die beiden Zählschleifen etwas 'früher' los, um das Skript nicht unnötig aufzublasen.)

Die Abbildung zeigt unmittelbar, dass jedes Sechseck aus einer Verschiebung des Originalsechsecks hervorgehen kann. Auch das Assoziativgesetz gilt.
T₁, T^-1₁, T^-2₁, ... T₂, T^-1₂, T^-2₂, ... sind Elemente einer Gruppe.



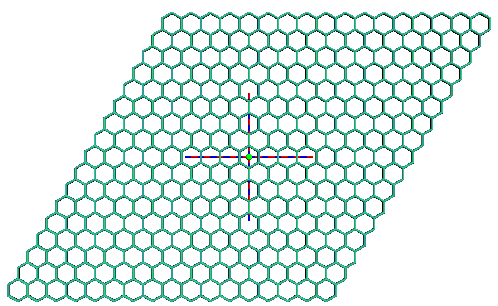
Hat man mal eine solche verschachtelte Zählschleife programmiert, kann man sie für die Verwendung verschiedener Objekte benutzen und so symmetrische Muster erzeugen.
Durch unsymmetrisch angeordnete Lichtquellen und deren Reflexe auf die Objekten ist die Symmetrie nicht so ganz gewahrt:



Durch starke Reflexion kommt man schon in die Nähe von WADA-Fraktalen:



Selbes Bild mit veränderter Kameraposition:




4. Kombination verschiedener Rotationen:
   Es ist unmittelbar einsichtig, dass das Hintereinanderausführen zweier Rotationen wieder eine Ratation ergibt.



5. Bermerkung 1:
   Die jeweils betrachtete Gruppe muss nicht kommutativ sein, es gilt jedoch das Assoziativgesetz.



6. Bermerkung 2:
   Die Menge aller Punkte, die durch Abbildung eines Punktes mit den Gruppenelementen erhalten werden kann, wird ORBIT bzgl. der betreffenden Gruppe genannt.



7. Konjugierte Transformationen:
   
   Siehe zunächst HIER.
   
   Die Abbildung T* = S T S ^-1 = S (T(S^-1(A))) wird KONJUGAT von T genannt, S die konjugierte Abbildung.
   Eine Anwendung ist die Abbildung der Fixpunkte 0 und unendlich auf die Fixpunkte -1 und 1, die im obigen Link vorgestellt wird.
   Ein gut verständliches Beispiels liefert Indra's Pearls S. 26 mit Hilfe eines Fliesenbodens.

Zum Vertiefen des Themas 'Objekte mit Symmetrie' hier noch ein Link zur Antrittsvorlesung v. P. Fiebig an der Uni Erlangen-Nürnberg von 2010.