Moebiustransformationen: Einfache Beispiele

Beispiel 1:
Für die komplexen Zahlen a,b,c,d wählen wir die folgenden Werte:

a = 1 + 0*i
b = 3 + 4*i (beliebig)
c = 0 + 0*i
d = 1 + 0*i

Aus



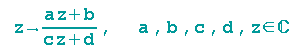
wir dann z' = z + b, d. h. eine Verschiebung.



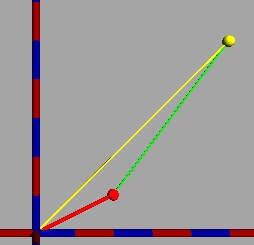
Unser Startpunkt (2/1) (z = 2 + 1i, in der Abb. rot) wird 3 nach rechts und 4 nach oben verschoben (Verschiebung in grün).

Mit dem ff. PoVRay-Makro kann man mit verschiedenen Werten experimentieren:

#macro moebius (ax, ay, bx,by,cx, cy, dx, dy, zx, zy,iter)
//z'= (az+b)/(cz+d), alle komplex

 #declare j=1;
 #while (j<iter+1)

 #macro produkt (ux, uy, vx,vy)
    #declare RE=ux*vx-uy*vy;
    #declare IM=ux*vy+uy*vx;
 #end


 //zähler berechnen
 produkt (ax,ay,zx,zy)
 #declare obenx=RE+bx; //Verschiebung dazu
 #declare obeny=IM+by;
 #undef RE
 #undef IM

 //Nenner berechnen
 produkt (cx,cy,zx,zy)
 #declare untenx=RE+dx; //Verschiebung dazu
 #declare unteny=IM+dy;
 #undef RE
 #undef IM


 #declare Radius=0.15;
 //Startzahl
 sphere { <zx,zy,0>, Radius pigment{Red*2} no_shadow}
 cylinder {<0,0,0> <zx,zy,0> 0.05 pigment {Red*2} no_shadow}


 //algebraische Formel für die Division zweier komplexer Zahlen a+bi und c+di:
 // a+bi   ac+bd      bc-ad
 // ---- = ------- +  ------- * i
 // c+di   c*c+d*d    c*c+d*d


 #declare zx_neu=(obenx*untenx+obeny*unteny)/(untenx*untenx+unteny*unteny);
 #declare zy_neu= (obeny*untenx-obenx*unteny)/(untenx*untenx+unteny*unteny);
 #declare mitte=<zx_neu,zy_neu,0>;


 //Startzahl
 sphere { <zx,zy,0>, Radius pigment{Red*2} no_shadow}
 cylinder {<0,0,0> <zx,zy,0> 0.025 pigment {Red*2} no_shadow}

 //möbiustransformiert
 sphere {mitte, Radius pigment{farbe} no_shadow}
 cylinder {<0,0,0> mitte 0.025 pigment {farbe*2} no_shadow}

 //Verschiebungsvektor dazu zeichnen:
 cylinder {<zx,zy,0> mitte 0.025 pigment {Green*2} no_shadow}

 #declare zx=zx_neu;
 #declare zy=zy_neu;



  #declare j=j+1;
  #end                   //end while

  #undef zx
  #undef zy
  #undef zx_neu
  #undef zy_neu


#end // end macro


union {
   //moebius (ax,ay,     bx,by,     cx,cy,      dx,dy,       zx,zy,      iter)
     moebius  ( 1,0,     3,4,       0,0,       1,0,          2,1,          1)
      }

Beispiel 2:
Für die komplexen Zahlen a,b,c,d wählen wir die folgenden Werte:

re(a) und im(a) ungleich Null
b = 0 + 0*i (beliebig)
c = 0 + 0*i
d = 1 + 0*i

Aus



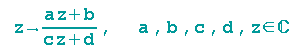
erhalten wir dann z' = az, d. h. eine Drehstreckung.

In der ff. Abbildung ist a=-3+4i in grüner Farbe abgebildet, Startzahl rot, az gelb.



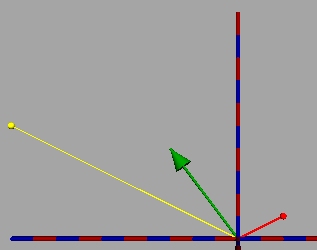
Unser Startpunkt (2/1) (z = 2 + 1i, in der Abb. rot) wird mit dem Faktor 5 gestreckt und um den Winkel, den a mit der reellen Achse bildet, gedreht.

Beispiel 3:
Wählt man im 2. Beispiel zusätzlich b von Null verschieden, dann kommt zur Drehstreckung noch eine Verschiebung dazu. Mit dem PoVSkript zur vorherigen Abbildung ist dies leicht durchführbar.

Beispiel 4: Spiegelung an der reellen Achse
Die komplexe Zahl z soll also durch die konjugiert komplexe Zahl ersetzt werden:
z_x + z_y*i wird zu z_x - z_y*i

a = 1 + 0*i
b = 0 - 2*z_y*i
c = 0 + 0*i
d = 1 + 0*i



Bei dieser Programmierung ist keine Iteration möglich (aber z würde eh nur "hin und her" gespiegelt werden).

Beispiel 5:
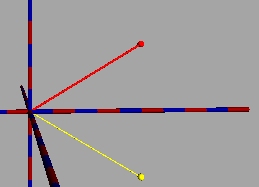
Für die Inversion am Einheitskreis (siehe Schaltfläche oben an der Seite) gilt die Abbildungsvorschrift:



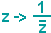
Auch sie kann durch eine Möbiustransformation realisiert werdern:

Um die komplexen Zahlen a,b,c und d für



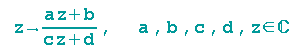
zu bestimmen, betrachten wir das Produkt aus z und der konjugiert komplexen Zahl zu z:



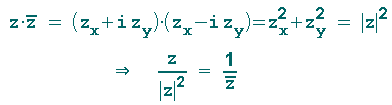
Vergleicht man das Ergebnis mit der Möbiustransformation, hat man sofort die gewünschten Zahlen a bis d:



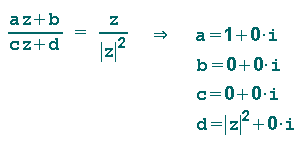
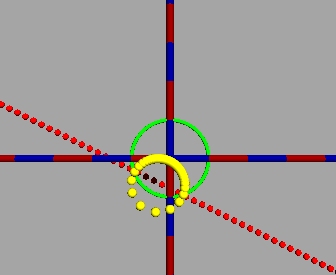
Rot: z, gelb: z', grün: Einheitskreis


Möglich ist es auch, die Abbildung



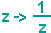
mit einer nachfolgenden Spiegelung an der reellen Achse stattdessen zu benutzen.

Im ff. Beispiel wird ein Mittelpunktskreis mit Radius 3 (rot) am Einheitskreis invertiert:



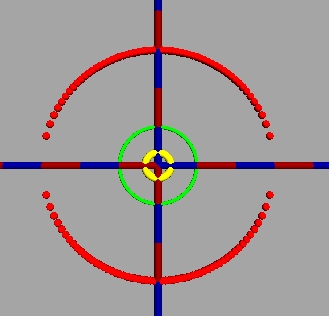
... und für diejenigen, die's mit povray nicht können, hier noch ein geogebra-Applet zur Inversion komplexer Zahlen am Einheitskreis:

Beispiel 6:
Variieren die darzustellenden komplexen Zahlen sehr stark (z.B. komplexe Widerstände in der Hochfrequenztechnik) , kann entweder eine logarithmische Skala benutzt werden oder aber man bildet mit einer Möbiustransformation die rechte Halbebene in den Einheitskreis ab.
Durch drei Punkte wird die gewünschte Möbiustransformation festgelegt:



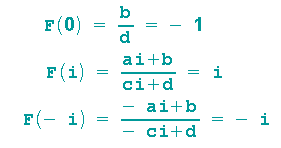
Also gilt:





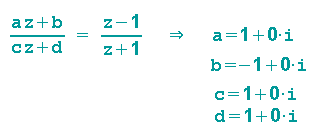
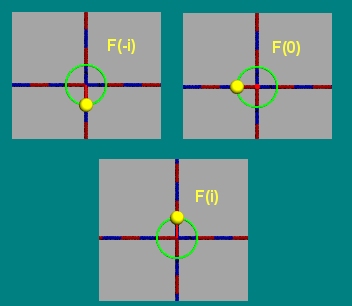
Wählt man nun irgendeine komplexe Zahl aus der rechten Halbebene, dann fällt ihr Bild in den Einheitskreis: (rot= Start, gelb=Bild)



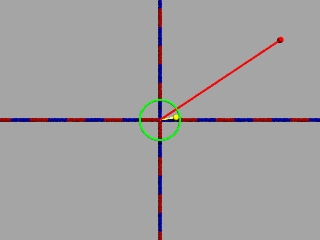
Die imaginäre Achse landet also auf der Kreislinie des Einheitskreises, die restliche rechte Halbebene im seinem Inneren, die reelle Achse wird auf sich selbst abgebildet.
Für komplexe Zahlen aus der linken Halbebene gilt dies nicht:



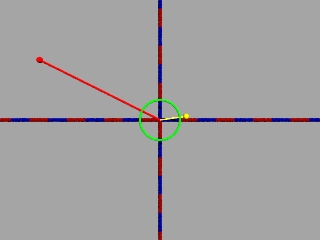
Geraden, parallel zur reellen Achse (Wirkwiderstand=konstant) werden auf Kreise abgebildet, die durch (1/0) laufen und den Einheitskreis senkrecht schneiden:



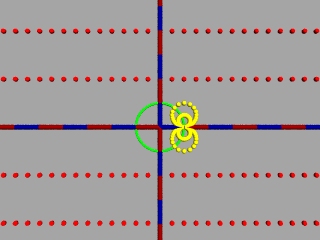
Parallelen zur imaginären Achse (Blindwiderstand=konstant) werden dagegen auf Kreise abgebildet, die die reelle Achse senkrecht schneiden:




Quelle zu diesem Beispiel: siehe Linksammlung (komplexe Analysis)

• Zum Seitenanfang