Moebiustransformationen

Bildet man das Bild unter einer Abbildung mehrmals wieder mit der gleichen Abbildung ab, dann erhält man eine sog. iterierte Abbildung.
Anders gesagt:
Wenn F unsere Abbildung ist, dann entsteht das (n+1)-Bild durch Anwendung von F auf das n-te Bild:
x _n+1 = F(x_n)

An Drehstreckungen sind wir bereits gewöhnt, also betrachten wir mal die Abbildung az, wobei a und z beides komplexe Zahlen sein sollen.

Für (fast) beliebig viele Iterationen kann man dann im PoVSkript mit dem Real- und Imaginärteil von a experimentieren und sich mehr oder weniger schöne Spiralen aus Drehstreckungen erzeugen. (Bemerkung: Wenn der Abstand von z' vom Koordinatenursprung zu klein ist, liefert das PoVSkript eine Fehlermeldung beim Zylinder.)



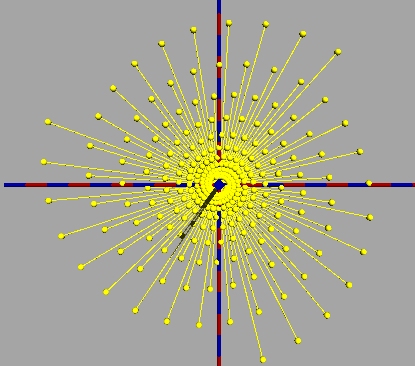
Wählt man a=z und addiert noch (-1/0/0) zum Kugelmittelpunkt dazu, dann hat man die Mandelbrotabbildung.
... und einige Spiralbilder sind nun auch programmierbar:
















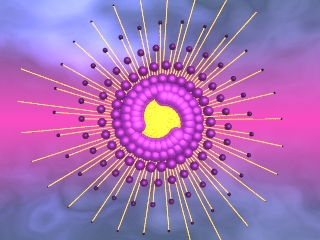
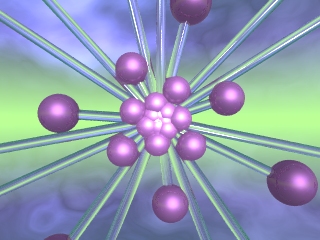
Die Startwerte für z bestimmen die Gestaltung der Spiralen: