Möbiustransformationen: Bezeichnungen

Erinnern wir uns zunächst an die Fixpunktgleichung aus dem vorletzten Kapitel:



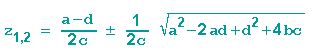
Stellt man den Radikanden etwas um (Addition von 0 in der Form +4ad-4ad), so erhält man:



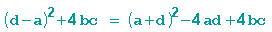
Die Summe a + d wird dabei Spur genannt. Mit Hilfe dieses Begriffes werden dann die Möbiustransformationen klassifiziert.

Sehen wir uns zunächst an, wie die Fixpunktgleichung mit Hilfe der Spur umgeformt werden kann: (beachte, dass ad-bc=1 sein soll, siehe vorletztes Kapitel )



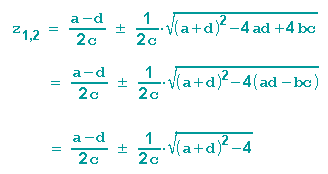
Die Einteilung:

Loxodromische MT haben 2 Fixpunkte, wir erhalten Spiralen vom Repellor zum Attraktor (engl.: source / sink).
Ihre Spur liegt außerhalb des Intervall [-2,+2].
Sie sind konjugiert zur Abbildung T(z) = az mit Betrag(a)>1.


Hyperbolische MT sind Spezialfälle der loxodromischen MT: Die Punktbahnen sind Kreise durch die Fixpunkte.
Ihre Spur ist reell und liegt nicht im Intervall [-2, +2] (Intervallgrenzen eingeschlossen).
Sie sind konjugiert zur Abbildung T(z) = az mit Betrag(a)>1.


Elliptische MT: Die Punktbahnen sind Kreise um die zwei neutralen Fixpunkte.
Ihre Spur ist reell und liegt im Intervall (-2, +2) (Intervallgrenzen ausgeschlossen).
Sie sind konjugiert zur Abbildung T(z) = az mit Betrag(a)=1.


Parabolische MT haben einen Fixpunkt, der gleichzeitig Repellor und Attraktor ist.
Ihre Spur ist +2 oder -2, also auch reell.
Sie sind konjugiert zur Abbildung T(z) = az + b mit Betrag(a)=1.