Moebiustransformationen

Wiederholung: Drehung, Streckung, Verschiebung, Drehstreckung

Die Technische Universität München bietet zum Thema einen interaktiven Lernpfad mit interaktiven cinderalla-Applets, den ihr HIER besuchen könnt.

Ein Video zur Veranschaulichung von Möbiustransformation findet man bei YouTube.

Wer will, kann über Möbiustransformation auch bei Wikipedia einiges finden.

Auf meiner Seite wieder ein erster leicht verständlicher Einstieg ins Thema für AnfängerInnen - keine erschöpfende Behandlung. Einige Visualisierungen und deren Programmierung mit PoVRay/GeoGebra werden vorgestellt.

Möbiustransformationen sind Abbildungen der Form:



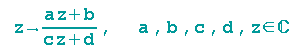
Bemerkung: Für c=0 und d=1 erhält man Ähnlichkeitsabbildungen, die also auch Möbiustransformationen sind.

Die Möbiustransformationen bilden eine Gruppe.

Einschub Gruppe

1. Auf einer Menge von Elementen ist eine Verknüpfung definiert, sodass die Verknüpfung zweier beliebiger Elemente wieder in der Ausgangsmenge enthalten ist (Abgeschlossenheit).
2. Es gibt ein neutrales Element.
3. Es gibt ein inverses Element.
4. Für je drei Elemente gilt das Assoziativgesetz.



Minibegriffserklärung:
a + 0 = a, d.h. 0 ist das neutrale Element der Addition.
a * 1 = a, d. h. 1 ist das neutrale Element der Multiplikation.

a + (-a) = 0, d. h. -a ist das inverser Element der Addition.
a * (1/a) = 1 für a von 0 verschieden, d. h. der Kehrwert von ist das inverse Element der Multiplikation.
In der Menge der ganzen Zahlen ist's also aus mit den multiplikativen inversen Elementen.

Assoziativgesetz: Bei Addition und Multiplikation dürfen Klammern verschoben werden.

Ein bisschen genauer kann man's auch bei Wikipedia nachlesen.

Um zu verstehen, was das Ganze soll, beginnen wir mit einigen Wiederholungen aus unserem Wissensvorrat:

Die Drehung:

Bewege mit gedrückter Maustaste die Ecke A_i des Dreiecks. Beim linken Dreieck ändern sich die Koordinaten aller Punkte der Dreiecksfläche, beim rechten Dreieck ist das Drehzentrum Fixpunkt, solange es innerhalb des Dreieckes liegt. Winkel und Längen der Strecken bleiben erhalten.

Die Verschiebung:

Ändere mit gedrückter Maustaste den Verschiebungsvektor oder die Ecken des Dreiecks ABC.





Die Streckung

Ändere mit gedrückter Maustaste den Streckfaktor am Schieberegler oder die Ecken des Dreiecks ABC.





Kombiniert man eine Drehung mit einer Streckung, so erhält man eine Drehstreckung:

Stelle mit gedrückter Maustaste am Schieberegler den Streckfaktor s und den Drehwinkel ein. Auch die Ecken des abgebildeten Dreiecks sind veränderbar.





Auch Punktspiegelung und Achsenspiegelung gehören zu den Abbildungen. Etwas interessanter wird es dann bei den komplexen Abbildungen.
Jetzt ist es an der Zeit, das Thema komplexe Zahlen zu wiederholen (klicke auf den entsprechenden Reiter oben an der Seite).

• Zum Seitenanfang