Möbiustransformationen: 1. Ein Beispiel mit 2 Fixpunkten
Um die immense Vielfalt der möglichen Möbiustransformationen einzuschränken, wählen wir als Beispiel eine MT mit 2 Fixpunkten. Damit wir auch ein paar Rechnungen anstellen können, soll für die Fixpunkte Folgendes gelten:
A = A' = -1 + 0i
B = B' = 1 + 0i
Die Parameter a,b,c und d seien so mit einem geeigneten Faktor multipliziert, dass d=1 gilt (siehe Kapitel "Freiheitsgrade einer MT" ). Aus den 6 möglichen reellen Freiheitsgraden werden somit 2 reelle Freiheitsgrade: Die Parameter a,b und c hängen davon ab, wie ein dritter Punkt C auf C' abgebildet wird.
Es gilt also:
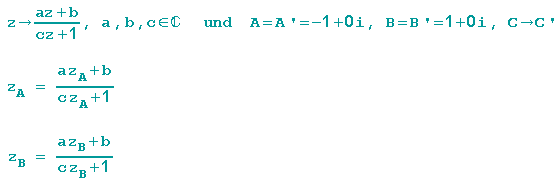
Für unsere Fixpunkte A und B setzen wir die obigen Werte ein und erhalten:
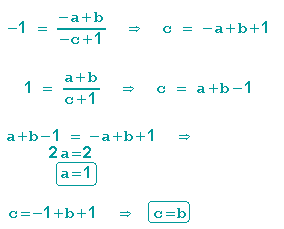
Mit diesem Ergebnis kann man nun im ff. Applet sehen, wie die MT von der Abbildung C zu C' abhängt: Im Menü "Ansicht" kann man die Algebra-Ansicht anzeigen lassen und sieht, dass der linke Fixpunkt bei ca. 30 Iterationsschritten erreicht wird.
|
|
Ändert man die Lage des Startwertes Z und die Lage von C und C' ein wenig, lässt sich wieder die Algebra-Ansicht zeigen, so erkennt man, dass nun der rechte Fixpunkt "angelaufen" wird:
|
|
Noch ein drittes Mal dasselbe Applet mit anderen Werten für Z, C und C':
|
|
Im bereits mehrmals erwähnten Lernpfad der TUM ist eine MT zusammen mit der inversen MT vorgestellt, beide Fixpunkte werden somit "angelaufen".
Möbiustransformationen: 2. Verschiebung eines Fixpunktes
Betrachten wir die Drehstreckung T(z)=az, a und z komplex, b=0, c=0 und d=1.
Solange der Betrag von a von 1 verschieden ist und a einen von Null verschiedenen Imaginärteil hat, ergibt die Iteration Spiralen zum Koordinatenursprung hin oder von ihm weg.
Damit der Fixpunkt O zu O+b hin verschoben wird, betrachten wir die Abbildung S(z)=z+b.
Verschieben wir erst mal z, führen dann eine Drehstreckung durch und machen die Verschiebung rückgängig:
T* = S( T( S -1 (z)))
T* = S( T(z-b) )
T* = S( a (z-b))
T* = a (z-b) + b
(bx / by) ist der Fixpunkt, T* ist eine affine Abbildung, d.h. ein Abbildung der Form T(z)= az+b (siehe Schaltfläche oben).
Bemerkung: Die Menge der affinen Abbildungen mit a ungleich Null bildet eine Gruppe (Siehe Schaltfläche oben, Link öffnet neues Fenster).
Das ff. Beispiel zeigt 2 Möbiustransformationen, eine davon mit verschobenem Fixpunkt.
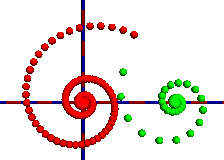
Der Kugelradius kann mit fortschreitender Iteration auch noch verändert werden:
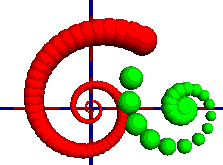
Möbiustransformationen: 3. Ein Beispiel für Fixpunktabbildung
Die Drehstreckung T= az ergibt Spiralen, die entweder zum Koordinatenursprung hin- oder von ihm weglaufen.
Die Fixpunkte O und "unendlich" sollen auf die Punkte (-1/0) und (1/0) abgebildet werden. Dies erreichen wir mit der folgenden Transformation:
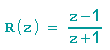
Durch Einsetzen von 0 und "unendlich" kann dies schnell überprüft werden.
Für die zu T = az konjugierte Abbildung müssen wir dann RTR-1 berechnen.
Zunächst brauchen wir also eine Formel für die Umkehrabbildung R-1 zu R:
-
Um ein bisschen mehr Vertrautheit und Erinnerung an's Thema "Funktion / Umkehrfunktion" zu erzeugen, verwenden wir vorübergehend die Buchstaben x und y:
Zu y suchen wir die Umkehrabbildung, wir vertauschen also x mit y und lösen dann wieder nach y auf:
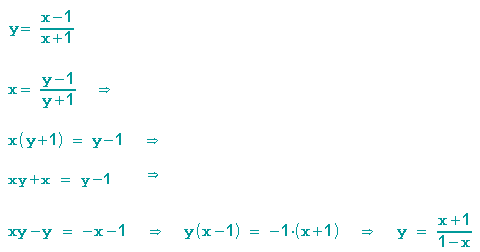
Die zweite Formel für y stellt also die Umkehrabbildung zu unserem "Start-y" dar.
Zurück zu unseren ursprünglichen Bezeichnungen: Für R(z) haben wir die Umkehrabbildung R-1(z) gefunden:
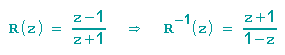
Zur Drehstreckung T=az können wir nun die konjugierte Abbildung berechnen:
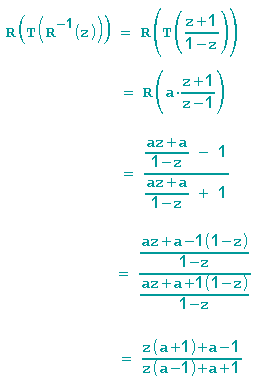
Im Buch Indra's Pearls kann man auf S. 66 die zugehörige Spirale am "Dr. Stickler" - Beispiel sehen. Nicht nur die Größe des Dr. Stickler, sondern auch seine Proportionen ändern sich, während er zu den beiden Fixpunkten läuft.
Benutzt man Kugeln und ändert den Radius in Abhängigkeit vom Iterationsschritt, dann erhält man bei geeigneten Startwerten Spiralem mit den gewünschten 2 Fixpunkten:
Ein bisschen schöner sieht das aus, wenn die Kugeln einander berühren.
Man kann sich dann fragen, wie der Abstand zwischen az und a2z aufgeteilt werden muss, um dies zu erreichen. Man kann es sich jedoch auch (mathematisch) einfacher machen, indem man die Punkte az und a2z als Berührpunkte ansieht: Die Kugelmittelpunkte liegen dann logischerweise genau in der Mitte der Berührpunkte, werden allerdings bei vielen Iterationswerten je nach Startwerten schnell sehr groß:

Sehen wir uns die zugehörigen Berechnungen an:
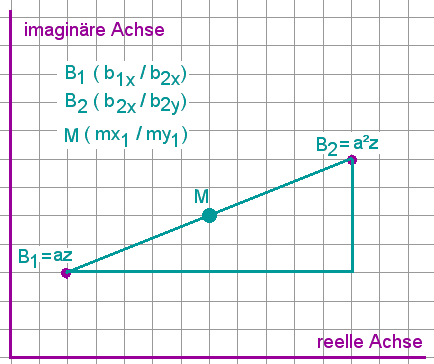
Wählt man die Bezeichnungen aus obiger Abbildung, dann gilt für die Koordinaten des Mittelpunktes:
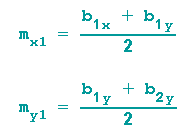
Für den halben Abstand zwischen az und a2z gilt dann:
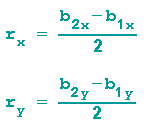
und der Kugelradius hat somit die Länge (Satz des Pythagoras)
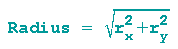
Das zur Abbildung gehörende Skript ist per Mausklick auf die Abbildung einsehbar.
Man kann dann mit verschiedenen Startwerten experimentieren und Spiralbilder erzeugen:

Bemerkung: Bei http://mygall.net/isabild ist dieses Bild auch zum Verkauf angeboten.
Möbiustransformationen: Ihre Fixpunkte
Um die Fixpunkte der allgemeinen Formel
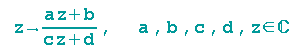
zu finden, muss die Gleichung
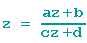
gelöst werden. Sie führt zu einer quadratischen Gleichung und wir verwenden die p-q-Formel zur Bestimmung der Lösungen:
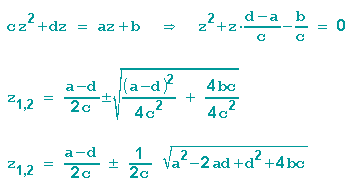
Da nun aber
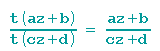
gilt, wählen wir t so schlau, dass die Determinante der Matrix
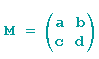
eins ergbit (siehe auch weiter oben).
Beispiel:
Für die Drehstreckung z = az gilt dann
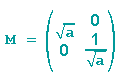
denn mit b=0, c=0 und d=1 folgt
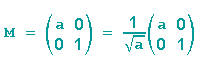
| © 2011-2024 Asti | PoVRay-Site | Mathematische Streiflichter | Algorithmische Kunst | Webdesign |