Fraktale und Iterationen - die allerersten Schritte

Betrachten wir die Iterationvorschrift z_n+1 = z_n² +c und entscheiden uns für einen Startwert z₀ und eine feste Zahl c, wobei z₀ und c komplexe Zahlen sein sollen.

z = 0,1 + 0 i
c = 0,1 + 0,7 i

Wir stellen noch eine weitere Bedingung: Der Betrag unserer komplexen Zahl muss kleiner als 2 sein.





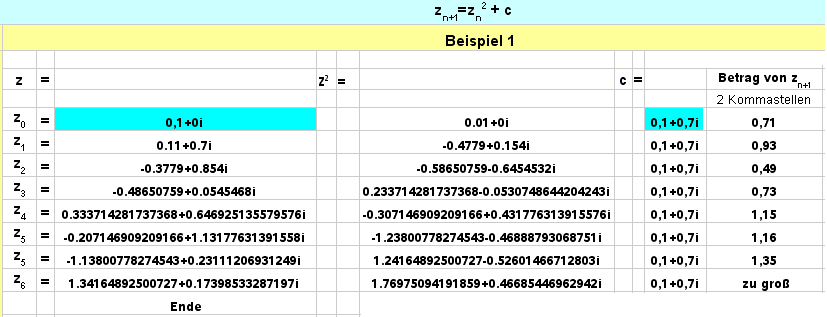
Diesmal haben wir einen Startwert z₀ erwischt, der Punkte auf der komplexen Ebene erzeugt,die ins Unendliche fliehen: Er gehört zur Fluchtmenge. (Sobald die Zahl 2 überschritten wird, wachsen die Beträge. Hier ersetzen wir einfach den Beweis durch Gutgläubigkeit.)

Machen wir einen 2. Versuch: Wir behalten unser z₀, verwenden aber c = 0,25 + 0,25 i Die Bedingung, dass der Betrag der komplexen Zahl kleiner sein soll als 2, wird beibehalten.



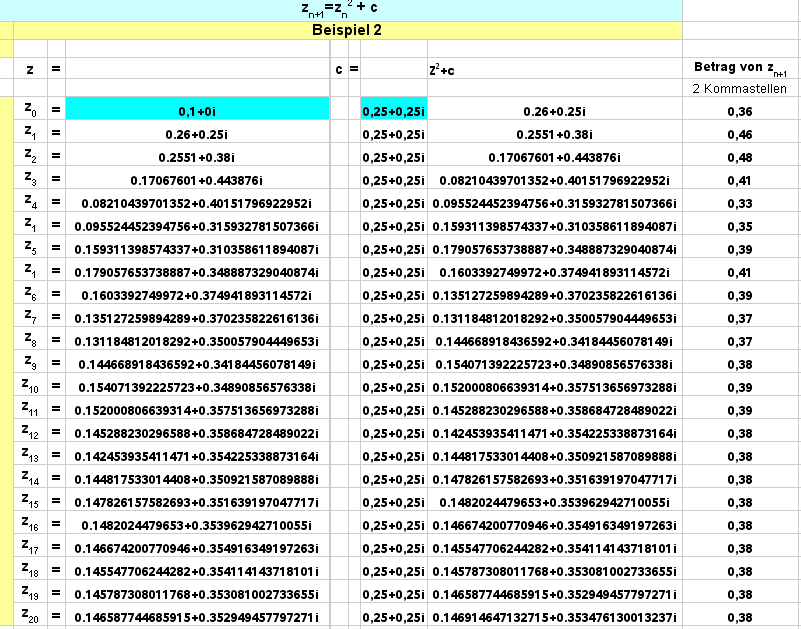
Wir sehen, dass zumindest für die ersten 20 Schritte keine Flucht ins Unendliche stattfindet: z_i "pendelt sich langsam ein".

Wir sind wieder gutgläubig und gehen davon aus, dass dieser Startwert für c zur Gefangenenmenge gehört.

Untersucht man nun das Verhalten der der komplexen Zahlenfolge z_n+1 = z_n² +c für alle Punkte der komplexen Zahlenebene, dann gibt es Werte c, die zur Fluchtmenge gehören, Werte c, die zur Gefangenenmenge gehören und Werte c, die die Grenze zwischen beiden bilden: die Juliamenge.