Der Pythagorasbaum als Einstieg in das Arbeiten mit Lindenmayersystemen
Die ff. Beispiele sind mit dem Programm "Lindenmayer 2.2e" (siehe Linkliste) erstellt.
-
Einschub: Die Befehle für Limdenmayer 2.2e:
Aus der Hilfe des og. Programms sind die ff. Befehle kopiert:

Es gibt 2 Dateneingabefelder: "L-Data" und "Axioms and Rules"
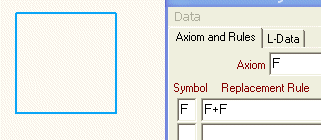
Wir nennen unser Axiom F und wählen F+F als Ersetzungsregel (siehe auch hier).
Wir erwarten das Zeichnen einer geraden Linie, danach eine Drehung um 90° gegen die Uhr, danach wieder das Zeichnen zweier geraden Linien nach je einer Drehung um 90° (denn im 2. Schritt wurde F ja durch F+F ersetzt). Mit dem Programm können die Iterationsschritte nacheinander gezeigt werden:
Als nächstes soll an der linken oberen Ecke unseres Quadrates ein zweites kleineres Quadrat gezeichnet werden, das nach links geneigt ist. Was muss geschehen?
- Die Schreibmarke, die nach dem Zeichnen des 1. Quadrates in dessen unterer rechter Ecke ist, soll zur Ecke oben links gehen, ohne dabei Linien zu zeichnen
- Die Schreibmarke soll dort ihre Richtung um 30° gegen den Uhrzeigersinn ändern.
- Die Zeichenlänge soll auf das 0,8-fache geändert werden.
- Jetzt soll wieder ein Quadrat gezeichnet werden.
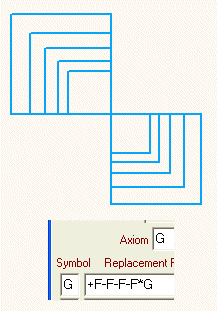
Wir nennen unser Axiom jetzt G, als Ersetzungsregel für G legen wir fest, dass zunächst F gezeichnet werden soll, dann lassen wir mit +f+f die Schreibmarke zur oberen linken Ecke des 1. Quadrates wandern, mit r* erfolgt die Drehung (Verkürzungsfaktor und 2. Winkel wurde vorher entsprechend eingestellt) und erhalten unser gewünschtes Ergebnis.
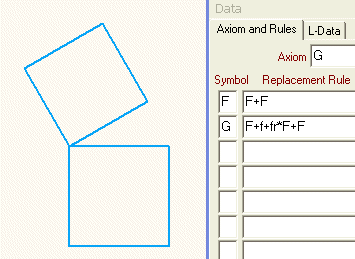
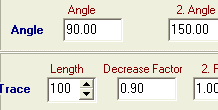
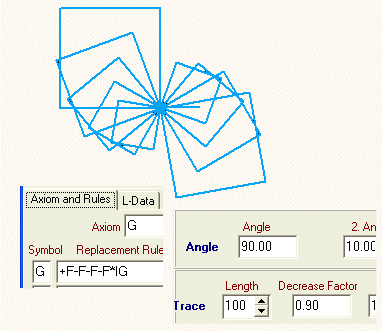
Wenn wir uns jedoch die Iteration schrittweise ansehen, dann ist das Ergebnis chaotisch und damit verbesserungsbedürftig.
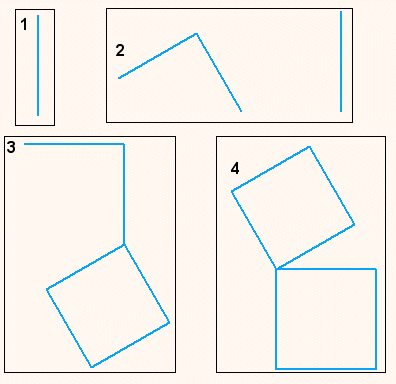
So soll es werden: Jeder neue Iterationsschritt soll ein neues Quadrat ergänzen:(Ersetzungsregel und Dateneingabe sind bei der Abbildung )
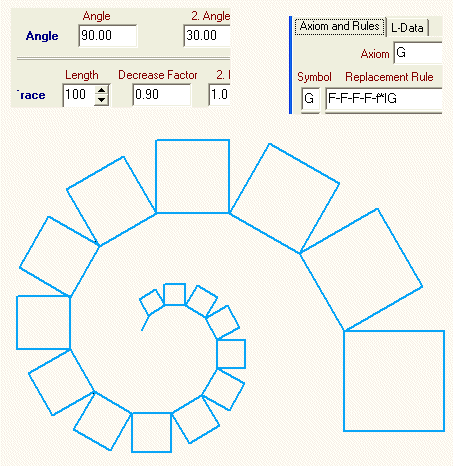
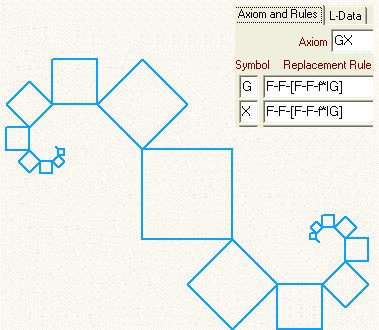
Einen Schritt weiter wollen wir noch gehen: Über jedem linken Kathetenquadrat soll zusätzlich ein rechtes Kathetenquadrat entstehen. Wir benutzten dafür die Befehle [ und ], mit deren Hilfe die Position der Schreibmarke gespeichert und wieder hergestellt werden kann. (Regel und Dateneingabe sind bei der Abbildung)
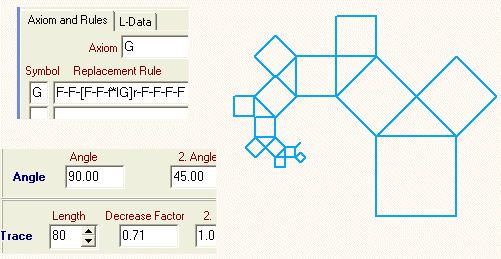
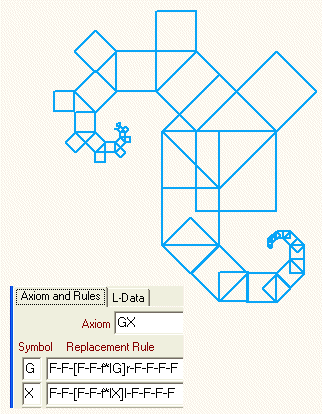
Was bei unserer Abbildung noch stört, ist die Linie, die an jedes Quadrat angehängt ist. Mit einem einfachen Trick lassen wir sie verschwinden: Im Axiom und in der Ersetzungsregel tauschen wir den Buchstaben G (G heißt ja "Linie zeichnen") durch den Buchstaben H (der erst in der Ersetzungsregel definiert wird):
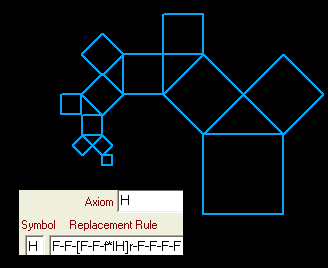
Zum Abschluss der Spielerei mit Quadraten noch einige Muster mit zugehörigen Regeln:
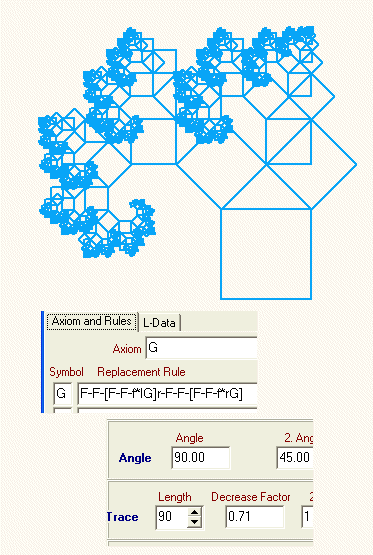
Suche dir aus den obigen Beispielen ein geeignetes heraus und versuche, daraus die Regeln für den Pythagorasbaum selbst zu entwickeln.
Der Pythagorasbaum
Bei den meisten Entwicklungsumgebungen für Lindenmayer-Systeme ist nur die Eingabe eines einzigen Winkels möglich. So auch bei FractalGrower. Dieses Java-Applet hat den Vorteil, dass bei jedem Iterationsschritt angezeigt wird, welches nun die aktuelle Zeichenkette ist. Der Nachteil ist, dass die Speicher-Funktion nicht funktioniert, dennoch halte ich es für empfehlenswert.
Der Befehlssatz weicht etwas von Lindenmayer 22e (Autor U. Schwebinghaus) ab und wird hier daher kurz vorgestellt:
-
f und h bewegen die Schreibmarke 1 LE vorwärts und zeichnen eine Linie.
g bewegt die Schreibmarke 1 LE vorwärts und zeichnet keine Linie.
+ und - ändern die Bewegungsrichtung nach rechts oder links im voreingestellten Winkel.
[ und ] merken die aktuelle Position und stellen sie wieder her (Ablage auf stack und Zurückholen)
a, b, c, d und e ändern die Farbe. Alle weiteren Kleinbuchstaben können in einer Ersetzungsregel definiert werden. Großbuchstaben sind verboten.
Etwas gewöhungsbedürftig ist der Vergrößerungsfaktor. Es gibt dazu einen Schieberegler, auf dem man dessen Kehrwert einstellen muss.
Da man für den symmetrischen Pythagorasbaum den Faktor 1 durch Wurzel 2 braucht, muss man Wurzel 2 einstellen!
Fangen wir an:
Schritt 1: Wir brauchen ein Quadrat q als Grundelement.
Anders gesagt: Zeichne eine Linie (aufwärts), drehe nach rechts (zweimal die voreingestellten 45°), zeichne wieder eine Linie, .... Also q=!++!++!++!++
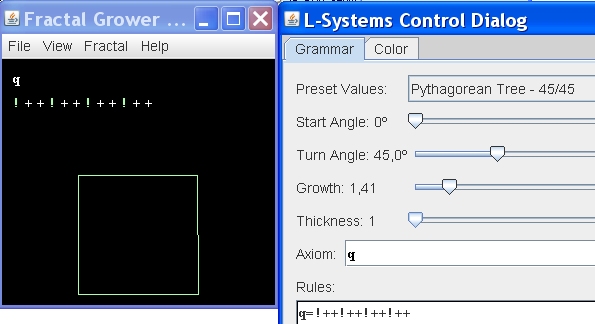
Die Blickrichtung des Cursors ist nach Abarbeiten der Formel nach oben gerichtet. Wir verwenden für's Linienzeichnen das Aufrufungszeichen, da das nächste Quadrat ja die mit Wurzel 2 reduzierte Länge haben soll.
Schritt 2: Das nächste Quadrat soll für den linken Ast an die obere linke Ecke gezeichnet werden, also müssen wir uns diese Position merken und vor dem Zeichnen des 2. Quadrates wieder herstellen!
q=![++!++!++!++]-q

Ein paar Schritte weiter (die Zeichenkette passt nun nicht mehr ins Bild):
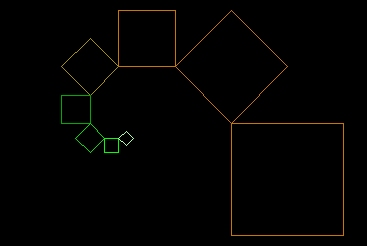
Schritt 3: Nun soll aber auch ein Quadrat an der oberen rechten Ecke unseres Startquadrates gezeichnet werden. Auch dieser Schritt muss fortgeführt werden. Also trennen wird das -p aus der ersten Ersetzungsregel ab und packen es in eine neue Regel:
q=![++!++!++!++]
r=-qr
... und wir erhalten dasselbe Ergebnis, so soll's ja auch sein!
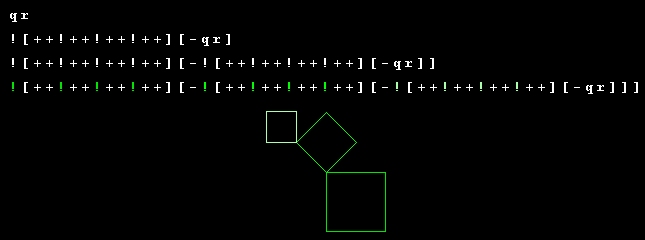
Nun könnten wir an die 2. Ersetzungsregel ja einfach ein [+qr] dranhängen, aber dann liegt das rechte Kathetenquadrat an der falschen Stelle:

... fügen wir nun einfach ein ! ein, wird's wieder falsch, da die gezeichnete Linie noch nicht verkürzt ist:
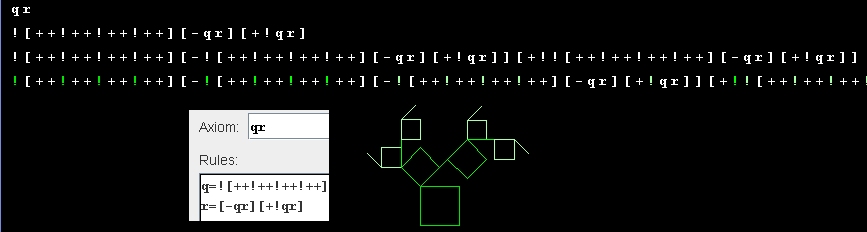
Wir müssen also +! als neue Ersetzungsregel einfügen: n=+!
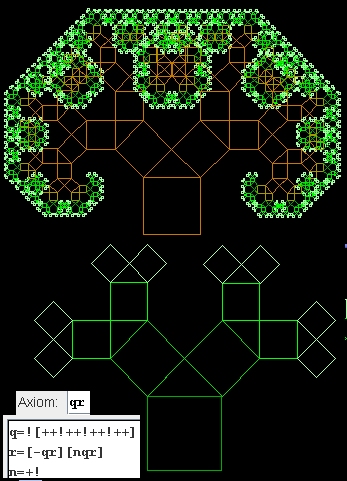
Bemerkung: Die farbliche Gestaltung wurde von FractalGrower erledigt.
Beispiele mit FractalGrower

Der Buchstabe e definiert die Farbe.
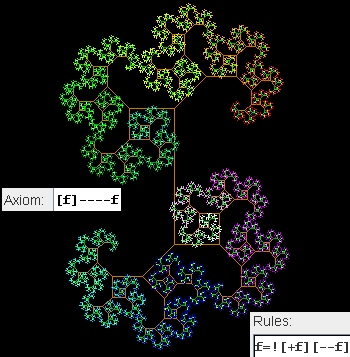



... und noch ein bei FractalGrower mitgelierfertes Beispiel: Dekking's Church:

| © 2009 Asti | Links für Unterricht | PoVRay-Site |