Einfache Regeln und Axiome für Lindenmayersysteme zum Mitdenken und Verändern

Die ff. Beispiele sind mit "Lindenmayer 22e" erstellt: Vgl. Linkseite.

Beispiel 1:



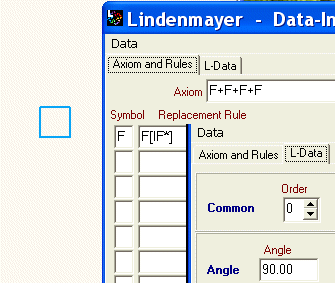
Axiom F: Zunächst wird eine Linie gezeichnet, die Schreibmarke ändert dann ihre Richtung um 90° gegen den Uhrzeigersinn, zeichnet wieder eine Linie,..., nach der 4. Linie ist ein Quadrat entstanden.

Ersetzungsregel: Wird nun die Anzahl der Iterationsschritte um 1 erhöht, dann kommt die Ersetzungsregel ins Spiel. Nach dem erstmaligen Zeichnen des Axioms (Quadrat) wird die Position gespeichert, danach erfolgt eine Drehung gegen den Uhrzeigersinn mit dem alternativen Winkel. Im diesem Beispiel ist er auf 45° eingestellt.
Nach der Richtungsänderung der Schreibmarke wird also an jeder Quadratecke wieder F gezeichnet, danach wird durch "*" die Linienlänge um den eingestellten Faktor gekürzt. Wirlich???? Nein, denn danach folgt vor der Wiederherstellung der Position keine F-Anweisung, "*" bleibt also schlichtweg wirkungslos.

Man erhält:



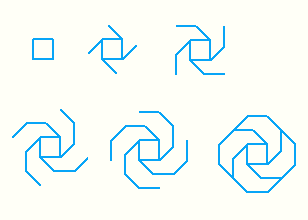
Beispiel 2:

Wir behalten unser Axiom (das Ausgangsquadrat bei), verändern aber die Position von "*". Den zweiten Winkel stellen wir auf 40° ein. Um die sukzessive Längenveränderung sichtbar zu machen, fügen wir vor dem Zeichnen von F ein "z" ein, um den Farbindex zufallsgeneriert zu ändern.



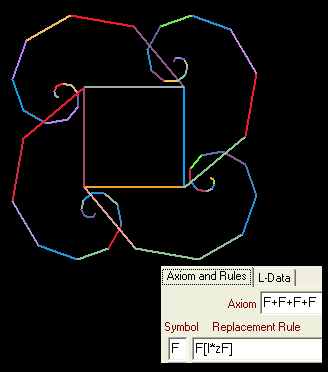
Beispiel 3:

Wir behalten wieder unser Axiom (das Ausgangsquadrat bei), wieder speichern wir bei der Ersetzungsregel die Position jeder Quadratecke, dieses Mal aber gleich zwei mal: Das 1. Mal wie gehabt mit nachfolgender Linksdrehung und Verkleinerung der Zeichenlänge. Das 2. Mal mit nachfolgender Rechtsdrehung und nochmaliger Verkleinerung der Zeichenlänge.
Gleichzeitig verkleinern wir den Drehwinkel.

Wir erwarten also, dass die Spiralen aus der Abbildung davor sich nicht so schnell zusammenringeln und dass die Spiralen, die nun nach rechts aus jeder Quadratecke wachsen, etwas kleiner sind. So ist es auch (Achtung: Nicht zu viele Iterationsschritte, sonst gibt's einen Programmabsturz!)



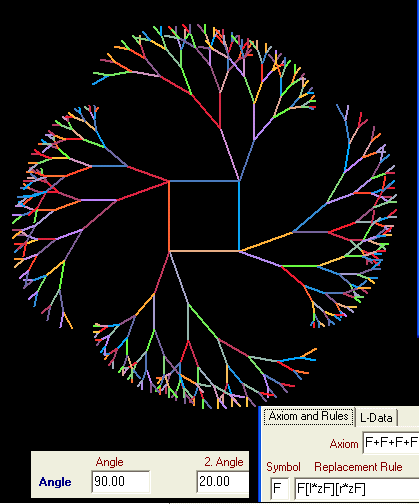
Beispiel 4:
Wir bringen am letzten Beispiel leichte Änderungen an: Der 2. Winkel wird vergrößert, das zweite Sternchen entfällt (die Spiralen nach rechts sollen gleiche Größe erhalten), als Verkleinerungsfaktor wird eine kleinere Zahl gewählt: Die Spiralen sollen nicht allzu groß werden:



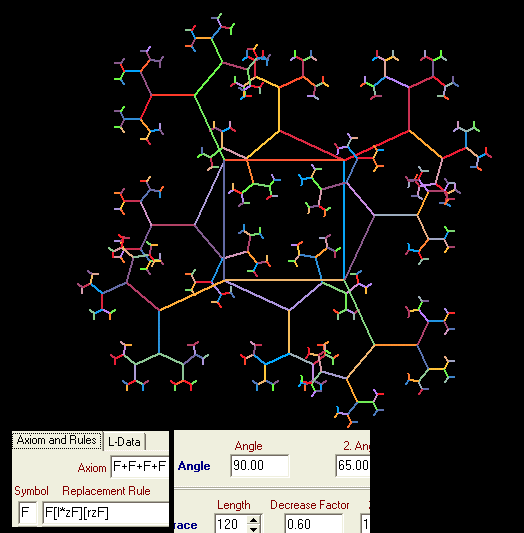
Nochmal dieses Beispiel mit anderen Daten:



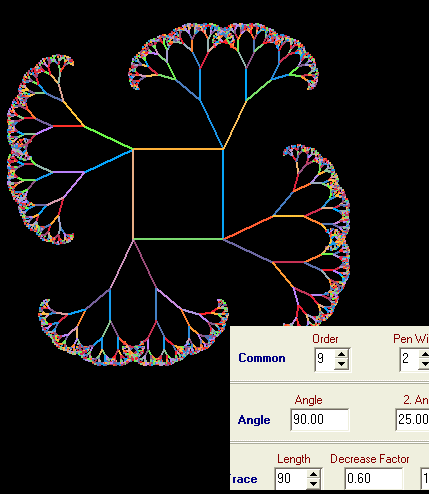
... und nochmal.



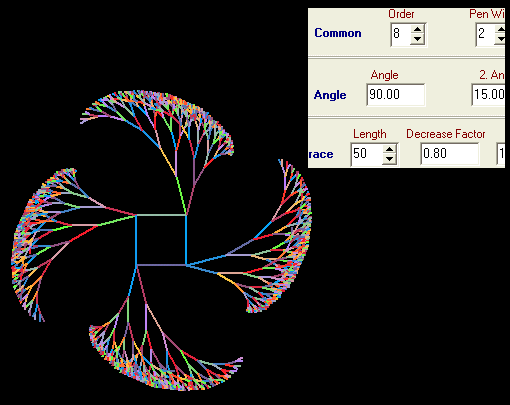
Beispiel 5:
Wir greifen auf die vorletzte Abbildung zurück (ohne das 2. Sternchen) und nehmen als Axiom statt eines Quadrates eine einfache Linie: Axiom = F, ... und erhalten einen Baum.



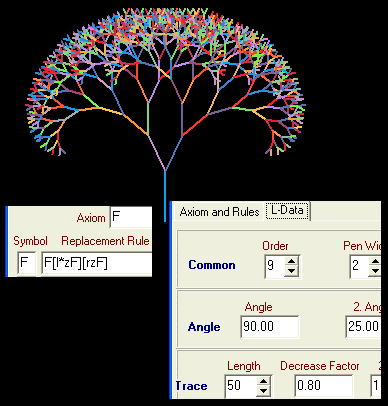
Beispiel 6:
Bei der Rechtsdrehung von F vergrößern wir den Winkel, indem wir mehrmals "r" einfügen:



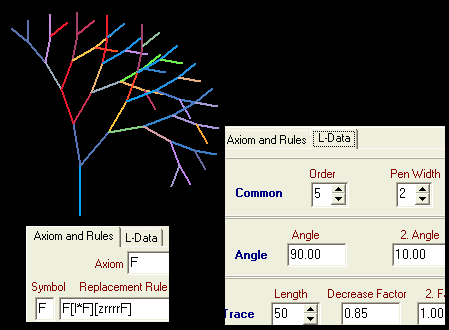
Beispiel 7:
Ersetzungsregel und Dateneingabe werden beibehalten, als Axiom benutzen wir jedoch F*F statt F: Unser Baum erhält nun einen zweiten Ast, der mit den verkleinerten Streckenlängen gezeichnet ist:



Beispiel 8:

Auf sehr einfache Art kann man Spiralen und Sterne in vielen Variationen zeichnen:

Wir nennen unser Axiom A und definieren die folgende Ersetzungsregel: Drehung um den vorgegebenen Winkel gegen den Uhrzeigersinn, Längenänderung von F entsprechend dem eingestellten Streckfaktor (Verkleinerungsfaktor) und Zeichnen von F, dann wieder von vorn.



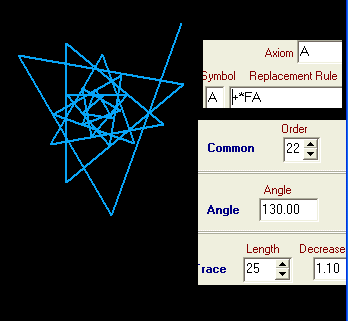
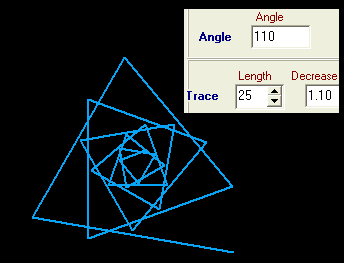
Bei den ff. Beispielen wird dasselbe Axiom benutzt, nur Winkel und Streckfaktor werden geändert:















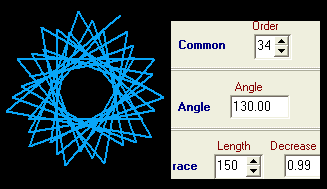
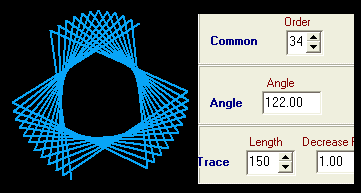
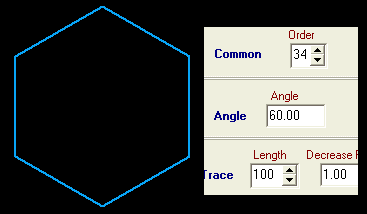
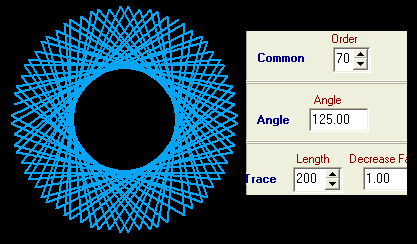
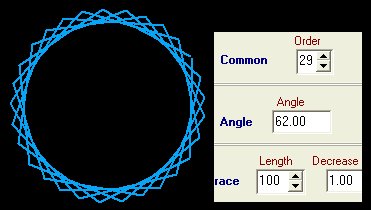
... na ja, und die mathematisch Interessierten können sich nun ihre Gedanken zu Hüllkurven oder auch zu Trochoiden machen. Viel Spaß!

Beispiel 9:

Und nochmal zurück zu Quadraten: Hier wurde "f" eingesetzt, um ohne zu zeichnen die Schreibmarke um die voreingestellte Länge weiter zu bewegen.