- affine Abbildung
- Fixpunkt
- gebrochene Dimension
- Iteration
- komplexe Zahlen
- Sierpinski-Dreieck
- Logarithmus
Programmierung von WADA-Fraktalen
TETRAEDER
Ziel 1:
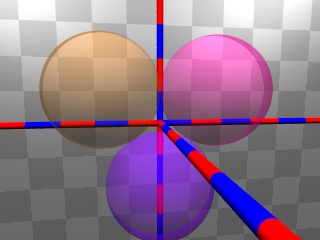
Drei gleichgroße Kugeln sollen symmetrisch zum Koordinatenursprung liegen und einander berühren, ihre Mittelpunkte sollen zunächst in der xy-Ebene liegen.
|
|
Die Kreismittelpunkte liegen auf einem Ursprungskreis mit Radius s:
x2 + y2 = s2,
die drei Vektoren vom Koordinatenursprung zu den drei Mittelpunkten M1, M2 und M3 schließen jeweils den Winkel 120° ein.
Es gilt also:
M1(x1/y1), M2(-x1/y1) und M3(0/-s)
Bei der Programmierung soll s als wählbare Größe vorgegeben werden, unbekannt sind dann der Kreisradius R und die Koordinaten des ersten Kreismittelpunktes M1(x1/y1). Wir brauchen also 3 Bestimmungsgleichungen, die diese Größen in Abhängigkeit von s liefern.
Ziel 2: Die drei Bestimmungsgleichungen
- x1 = R, siehe Abbildung
- Der Winkel zwischen x1 und der Verbindungslinie von O zu M1 (in der Abbildung mit s bezeichnet) beträgt 30°.
Mit sin 30° = y1 : s = 0,5 folgt: y1 = s : 2 - Aus dem Satz des Pythagors folgt: s2 = R2 + y12
Ziel 3: Das Lösen der 3 Bestimmungsgleichungen
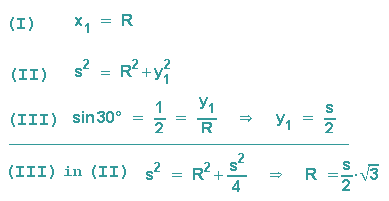
Für die Koordinaten der drei Kugelmittelpunkte gilt also:
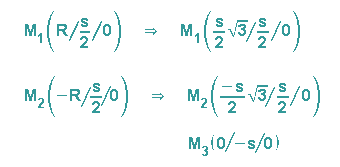
Ziel 4:
Die Kugeln sollen auf - nicht in- der xy-Ebene liegen, d.h. sie müssen um R in z-Richtung verschoben werden.
Wegen des linkshändigen Koordinatensystems von PoVRay werden sie um R Längeneinheiten in die minus-z-Richtung verschoben. Für ihre neuen Mittelpunkte gilt also:
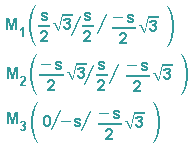
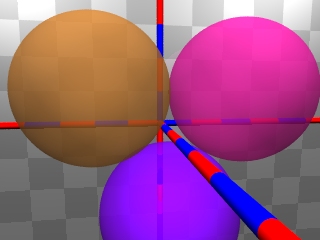
Ziel 5:
Die Kamera soll aus der minus-z-Richtung in die Lücke zwischen den drei Kugeln sehen, dahinter soll sich eine 4. gleichgroße Kugel befinden. Für ihren Mittelpunkt gilt also:
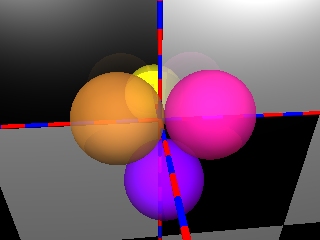
Das Makro (Prozedur), die Deklarationen und die Ebene haben also den ff. Programmcode:
#declare Farbe1= color SpicyPink transmit 0.4;
#declare Farbe2= color Gold transmit 0.4;
#declare Farbe3= color MediumSlateBlue transmit 0.4;
#declare Farbe4= color Yellow transmit 0.4;
#macro Kugeln(s, Farbe1, Farbe2, Farbe3, Farbe4)
#local x1= s/2*sqrt(3);
#local y1= s/2;
#local z1=-s/2*sqrt(3);
#local x2= -s/2*sqrt(3);
#local y2= s/2;
#local z2=-s/2*sqrt(3);
#local x3= 0;
#local y3= -s;
#local z3=-s/2*sqrt(3);
#local x4= 0;
#local y4= 0;
#local z4= s*sqrt(3);
#local M1=<x1,y1,z1>;
#local M2=<x2,y2,z2>;
#local M3=<x3,y3,z3>;
#local M4=<x4,y4,z4>;
#local R=s/2*sqrt(3);
union{
sphere {M1 R pigment{ Farbe1}}
sphere {M2 R pigment{ Farbe2}}
sphere {M3 R pigment{ Farbe3}}
sphere {M4 R pigment{ Farbe4}}
no_shadow
}
#end
Kugeln (2, Farbe1, Farbe2, Farbe3, Farbe4)
plane {z,0.01
pigment {checker White transmit 0.2 Clear scale 8}
finish{F_MetalA}
}
Um schöne Bilder zu erhalten, werden nun die Kugeln mit spiegelnder Oberfläche versehen und die Kamera auf die minus-z-Achse positioniert: (Skript bei Mausklick auf das Bild)

Das Skript bietet nun viele Variationsmöglichkeiten: Ändern des Kugelradius, Ändern der Kameraentfernung, "Störung" der Lichtstrahlen zwischen Kamera und Objekt, Änderung von Kugelfarbe und -oberflächenbeschaffenheit. Im Folgenden einige Beispiele dazu. Bei Mausklick auf das Bild ist jeweils das zugehörige Skript einsehbar.










OKTAEDER
Wer eher an schönen Bildern und weniger an "chaotic scattering" oder "wada basins" interessiert ist, kann auch anstelle der 4 gleichgroßen einander berührenden Kugeln noch eine vierte Kugel hinzunehmen, sodass ein Oktaeder entsteht. Die Position der Kamera darf dann nicht mehr auf der minus-z-Achse sein, sondern muss zu einer "Lücke" geschoben werden.
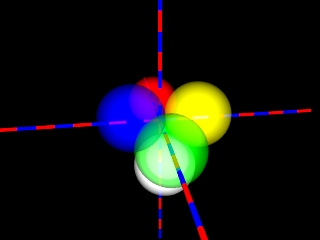
In der zweiten WADA-Galeriewerden hierzu einige Bilder gezeigt.
WÜRFEL
Einfacher geht's mit der Kamerapositionierung, wenn man 8 Kugeln in die Ecke eines Würfels setzt, auch hierzu gibt's Beispiele in der zweiten WADA-Galerie.
| © 2009 - 2024 Asti | PoVRay-Site |