- affine Abbildung
- Fixpunkt
- gebrochene Dimension
- Iteration
- komplexe Zahlen
- Sierpinski-Dreieck
- Logarithmus
Die Begriffe, die einem bei Beschäftigung mit dem Thema immer wieder begegnen:
- Fraktal, Attraktor
- Gefangenenmenge, Fluchtmenge, Juliamenge
- Apfelmännchen, Mandelbrotmenge und Einfärbung
- Iterierte Funktionensysteme, IFS
1. Gefangenenmenge, Fluchtmenge und Juliamenge:
Betrachtet man eine komplexe Zahl z und die Iterationsvorschrift
zn+1 = zn2
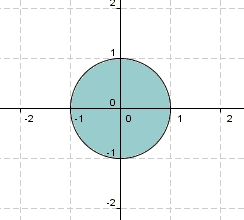
dann hat man die Qual der Wahl, mit welchem Startwert man beginnt. Wählen wir als erstes mal einen Startwert im Innern des Einheitskreises, d. h. eine komplexe Zahl z, deren Betrag kleiner als 1 ist.
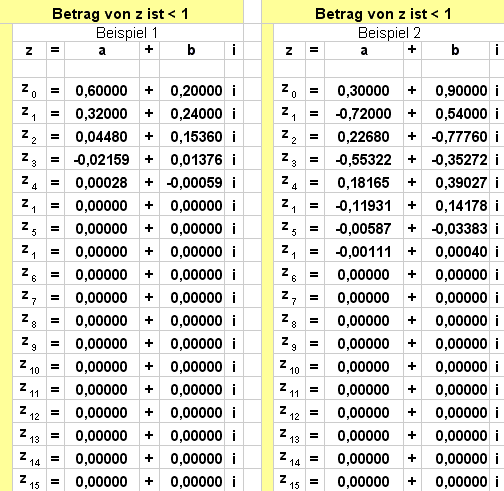
Sieht man sich die Zeigermultiplikation zweier komplexer Zahlen an, dann wird klar, dass die Zahlenfolge den Einheitskreis nicht verlassen kann. All diese Startwerte bilden daher eine Gefangenenmenge.
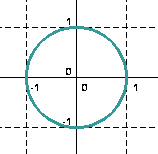
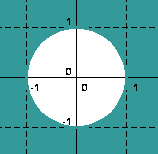
Ist der Betrag von z gleich 1, dann springen die Punkte der obigen Iterationsvorschrift auf der Kreislinie des Einheitskreises hin und her:
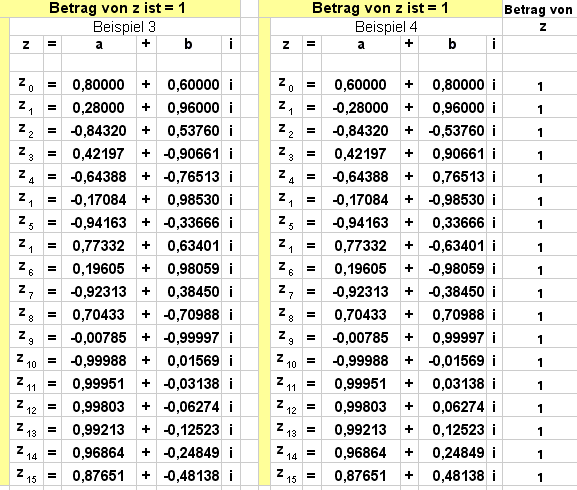
Die Kreislinie bildet die Grenze zwischen Gefangenen- und Fluchtmenge (s.u.) und wird Juliamenge (von Gaston Maurice Julia und Pierre Fatou erstmalig beschrieben) genannt. Für andere Iterationsvorschriften sieht die Juliamenge auch interessanter aus. Hier findest du online-Beispiele.
Ist der Betrag des Startwertes größer als 1, dann fliehen nicht nur die Punkte aus dem Einheitskreis ... auch das Tabellenkalkulationsprogramm ergreift schnell die Flucht:
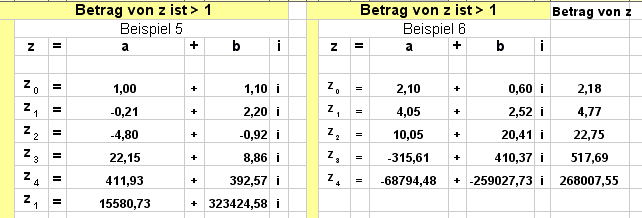
Diese Menge wird Fluchtmenge genannt.
Verallgemeinert gilt:
Wenn f ein Polynom mindestens 2. Grades ist, dann heißt die Menge derjenigen Anfangswerte, für die die Iterationsfolge beschränkt ist, ausgefüllte Juliamenge. Ihr Rand wird als Juliamenge von f bezeichnet.
Mandelbrotmenge
Man kann nun auch die Iteration zn+1 = zn2 + c - mit c komplex und von Null verschieden - betrachten.
Dazu erst mal einige Bildbeispiele, an denen man erkennt, dass die Wahl von c das Aussehen der Gefangenenmenge und damit auch der Juliamenge (Rand) bestimmt.
Bilder mit Ultrafractal erstellt:


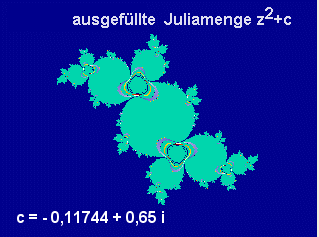

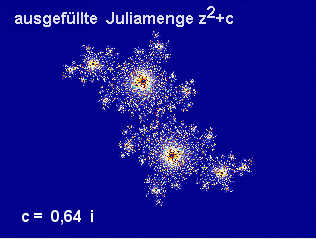
Bemerkung: Man beachte die Symmetrie zum Koordinatenursprung!
Je nach Wahl des Startwertes ist die entstehende Juliamenge für zn+1 = zn2 + c zusammenhängend oder nicht zusammenhängend.
Wählt man nun z0=0 und fasst man all diejenigen Startwerte c zusammen, die bei beschränkter Iterationsfolge eine zusammenhängende Juliamenge ergeben, spricht man von einer Mandelbrotmenge (der Form wegen auch als "Apfelmännchen" bekannt).
Für unser Beispiel zn+1 = zn2 + c gilt also formal:
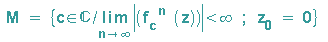
... und wie kommt nun die Farbe ins Bild?
Stellt man sich die Punkte (des Monitors) als komplexe Zahlen vor, dann nimmt man sich zunächst diejenigen Werte für c vor, für die die Iterationsfolge beschränkt bleibt und färbt sie z.B. schwarz ein.
Berechnet man die Folgenglieder mit einem PC-Programm, so muss man eine Abbruchbedingung setzen: Gilt für die Zahlenfolge z.B. nach nmax=100 Iterationsschritten noch, dass der Betrag von c kleiner als 2 ist, so wählt man Schwarz als Farbe.
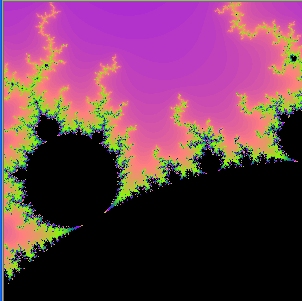
Ist bereits nach i Schritten (i < nmax ) der Betrag 2 erreicht, dann wird i eine Farbe zugeordnet und die entsprechende komplexe Zahl c in dieser Farbe eingefärbt .... und schon werden die Apfelmännchen bunt:
Hier eine Folge von Vergrößerungen, die mit Fractal Explorer (vgl. Linkliste) gemacht wurde:
 |
 |
 |
 |
 |
 |
Sehr schön werden solche Vergrößerungen auch mit diesem Java-Applet gezeigt.
| Bild 1 |
| Bild 2 |
| Bild 3 |
| Bild 4 |
2. Iterierte Funktionensysteme (IFS)
Wendet man eine Funktionsvorschrift auf einen Startwert an, nimmt das zugehörige Ergebnis und wendet darauf nochmal die Funktionsvorschrift an, usw., dann spricht man von Iteration.
Nun kann man statt einer einzigen Funktionsvorschrift f auch verschiedene Funktionen f1, f2, f3, ... benutzen. Man hat dann ein Iteriertes Funktionensystem (IFS).
Michael Barnsley stellte sie 1987 vor.
Fraktal und Attraktor
Fraktale Formen oder Muster haben eine hohe Selbstähnlichkeit (Teile der Form sind Kopien der Gesamtform), evtl. eine exakte Selbstähnlichkeit (jeder beliebige Teil der Form enthält eine Kopie der Gesamtform), ihre Dimension ist nicht ganzzahlig sondern gebrochen.
Ein bekanntes Beispiel ist das Farnblatt. Schneidet man einen Farnwedel heraus, dreht und vergrößert ihn, so kann man nicht mehr erkennen, ob nicht doch das Originalfarnblatt vorliegt.

Auch das folgende Kreuz ist ein solches Beispiel:

Spielt man das Würfelspiel zum Sierpinksi-Dreieck, dann entsteht die ff. bekannte Figur, die dann ATTRAKTOR genannt wird. Die exakte Selbstähnlichkeit wird hier wie auch beim Kreuz nur durch die Auflösung des Monitors oder auch durch die Anzahl der Iterationsschritte begrenzt.

| © 2009 Asti | Links für Unterricht | PoVRay-Site |