Ellipsen

Auch eine Ellipse lässt sich als Hüllkurve ihrer Tangenten darstellen, auch hier wird durch die Tangentennormalen die Evolute sichtbar.

Zur Programmierung einer den Sachverhalt darstellenden Animation muss die Funktionsgleichung (obere Hälfte der Ellipse) abgeleitet werden:

Methode 1: Die implizite Ableitung



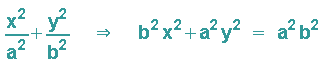
Unter Beachtung der Kettenregel erhält man dann für die Ableitung:



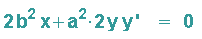
In diese Gleichung kann man



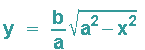
einsetzen und erhält:



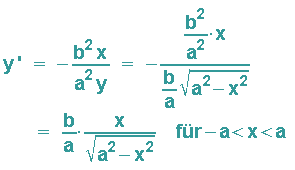
Methode 2: Die explizite Ableitung



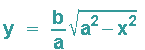
ist die Gleichung der oberen Ellipsenhälfte. Diese wird unter Beachtung der Kettenregel und der Ableitungsregel für Potenzfunktionen abgeleitet:

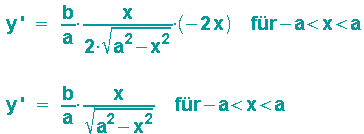
Für eine konkrete Animation mit Darstellung von Tangenten, Tangentennormalen und Evolute soll das Beispiel a=1 und b=2 betrachtet werden. Für die Ellipsengleichung gilt dann:

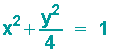bzw.

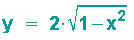
Der Punkt



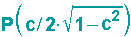
liegt also für -1<c<+1 auf der Ellipse. Für die Steigung m_c im Punkt P gilt dann:



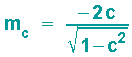
An der Formel erkennt man, dass sich für negative c eine positive Tangentensteigung und für positive c eine negative Tangentensteigung ergibt. Für c=0 verläuft die Tangente waagrecht, für c=1 bzw. c=-1 hat sie die Gleichung x=-a bzw. x=a mit a=1.

Setzt man das Ergebnis für m_c in die Punkt-Steigungsgleichung ein, so erhält man:





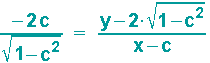
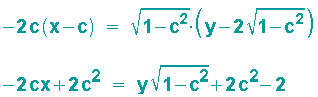
Als Tangentengleichung ergibt sich dann:

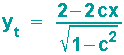
Um die Evolute sichtbar zu machen, braucht man noch die Gleichung der Tangentennormalen. Ihre Steigung ist der negative reziproke Wert der Tangentensteigung:



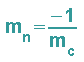
Setzt man dies in die Punkt-Steigungs-Gleichung ein, so erhält man



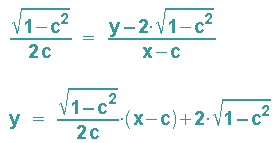
und kann nun mit Hilfe der Tangentennormalen die Evolute der Ellipse als deren Hüllkurve sichtbar machen, auf der dann die Krümmungskreismittelpunkte liegen:

Bewege mit gedrückter Maustaste den Punkt auf dem Schieberegler.

Über den Menüpunkt EVOLUTE ist die Evolute der Ellipse als Ortskurve der Krümmungskreismittelpunkte in einer Animation zu sehen.

• Zum Seitenanfang