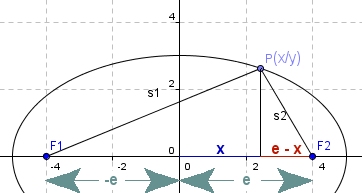
Bezeichnungen an der Ellipse
Die Menge aller Punkte, deren Abstand von einem Brennpunkt F das n-fache des Abstandes zu einer fixen Geraden g ist, ergibt eine Ellipse für n<1.
Ellipsendefinitionen und Konstruktionen:
Man erhält eine Ellipse nicht nur als Schnittkurve einer Ebene mit einem Kegel: Die Menge ihrer Punkte hat von 2 Brennpunkten F 1 und F 2 eine konstante Abstandssumme: Bewegt man den Punkt P mit gedrückter Maustaste, so sieht man links in der Abbildung, dass die Summe aus s1 und s2 immer konstant ist und 2a beträgt.
Aus der Abstandssummendefinition der Ellipse kann sie dann auch konstruiert werden: Bewege den Punkt Q bei der Fadenkonstruktion mit gedrückter Maustaste.
Variante 1: Die Fadenkonstruktion
Denkt man sich die Enden eines Fadens in den beiden Brennpunkten befestigt und einen Zeichenstift so, dass er den Faden spannt (in der Abbildung im Punkt E1 für den oberen Ellipsenteil), dann entsteht bei der Bewegung des Stiftes eine Ellipse.
Variante 2: Die Hauptkreiskonstruktion (Konstruktion mit 2 Kreisen)
Ein Mittelpunktskreis x2 + y2 = b2 mit dem Radius b wird im Verhältnis b:a gestaucht (... oder der kleinere Kreis wird gestreckt.).
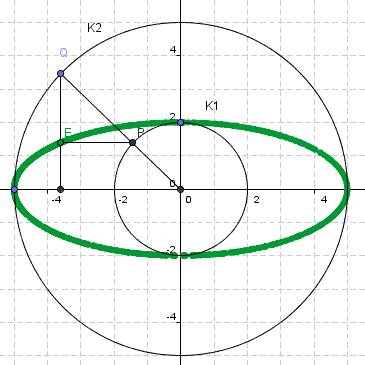
Die Kreisradien seien a und b. Sie ergeben dann die halben Hauptachsen der Ellipse.
Es gilt also
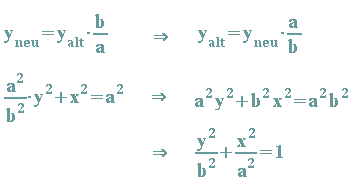
Aus dieser Überlegung folgt die Hauptkreiskonstruktion der Ellipse: Der Link führt diese Konstruktion dynamisch durch.
Bewege mit gedrückter Maustaste den Punkt Q auf dem größeren Kreis: (Aus Gründen der Übersichtlichkeit wird in der Abbildung nur der obere Ellipsenteil dargestellt.)
Variante 3: Parameterdarstellung und Mittelpunktsgleichung
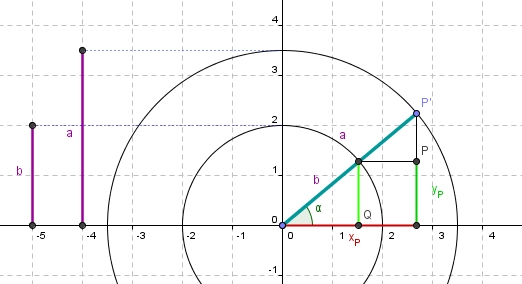
Aus der obigen Abbildung ergibt sich die Parameterdarstellung der Ellipse. Durch Quadrieren der Gleichungen erhält man dann die Mittelpunktsgleichung:
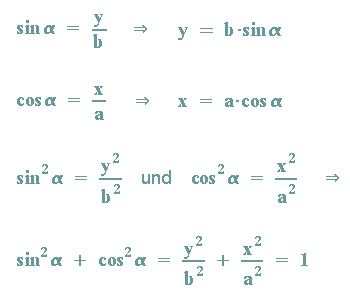
Herleitung der Mittelpunktsgleichung aus der Fadenkonstruktion
Mit Hilfe des Satzes von Pythagoras erhält man:
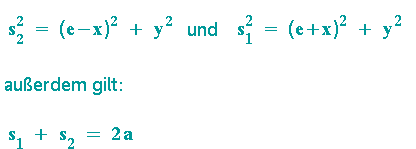
Im nächsten Schritt zieht man aus den beiden oberen Gleichungen die Wurzel. Anschließend addiert man s1 und s2 und setzt das Ergebnis gleich 2a.
Da die so erhaltene Gleichung gleich zwei Wurzeln enthält, wird eine der beiden Wurzeln auf die linke Seite gebracht und man erhält:
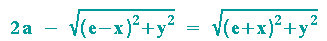
Diese Gleichung wird nun quadriert (an die 2. binomische Formel auf der linken Seite denken!), die Klammern werden ausmultipliziert, die Minusklammer wird aufgelöst, passende Terme werden zusammengefasst. Man erkennt dann, dass man das Ergebnis dur -4 teilen kann und erhält:
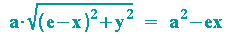
Diese Gleichung wird nun quadriert und die Klammern werden ausmultipliziert. Nach Vereinfachung und Sortieren der Summanden kann a2 ausgeklammert werden:
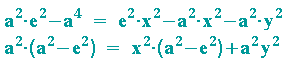
Wegem des Satzes von Pythagoras
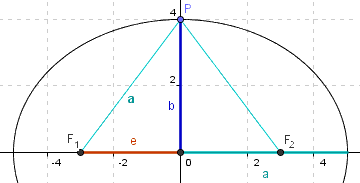
gilt
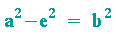
Dies wird nun in die letzte Gleichung eingesetzt.
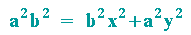
Nach Division durch a2b2 erhält man die Mittelpunktsgleichung:
| © 2009 Asti | Links für Unterricht | PoVRay-Site |