Hüllkurven und Evoluten
für Kegelschnitte und beim Huygensschen Prinzip
Mit Hilfe von Geraden können gekrümmte Linien, Hüllkuven, entstehen. Ein "Schnurbild" als Beispiel:
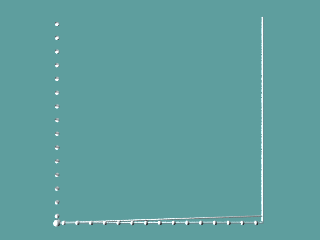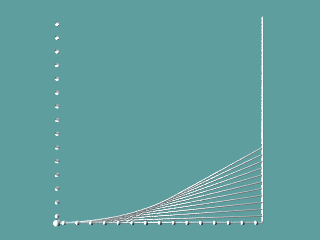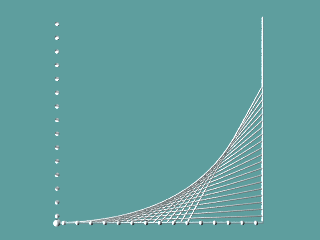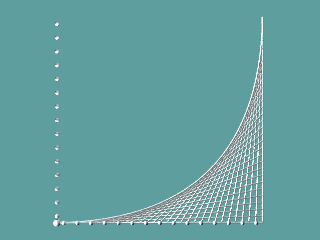
Zeichnet man zu einer differenzierbaren Funktion/Relation ihre Tangenten, so stellt man fest, dass die Funktion als Hüllkurve ihrer Tangenten erscheint:
Im Folgenden sollen die Kegelschnitte Parabel, Ellipse und Hyperbel vorgestellt werden.
Parabel mit Hüllkurve und Evolute
In der folgenden Animation werden für b = 0,2 die Tangenten
yt = 2ab xt -a2b
gezeichnet, a variiert dabei von -4 bis +4. Dabei entsteht als Hüllkurve
y = bx2.
Vgl. "math. Überlegungen" im Menü auf der linken Seite.

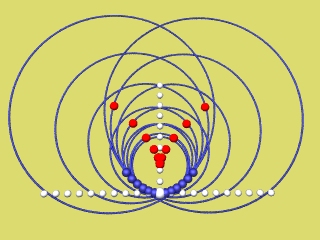
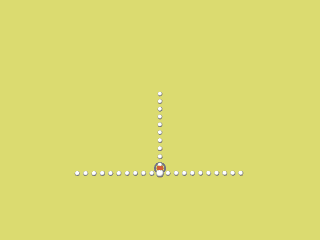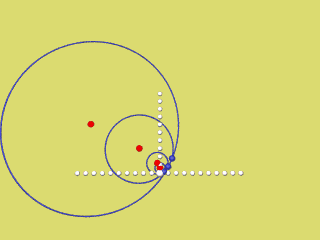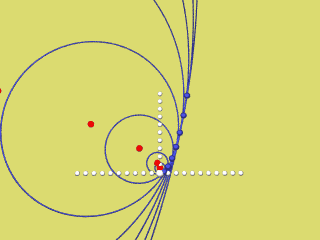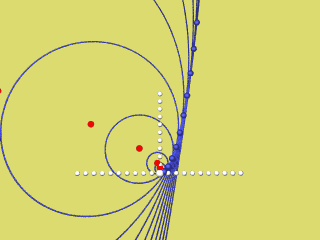
Zeichnet man zur selben Parabel die Evolute (rot) und die zugehörigen Krümmungskreise, so erkennt man, dass die Parabel auch gleichzeitig die Hüllkurve ihrer Krümmungskreise ist:
 |
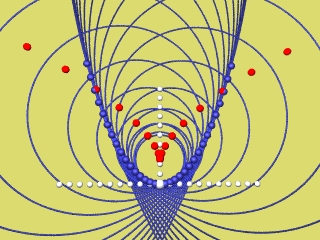 |
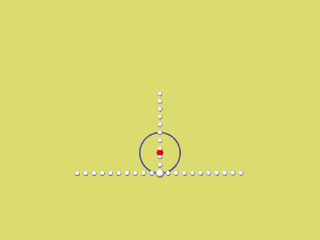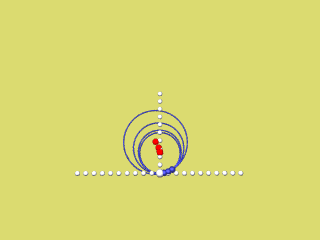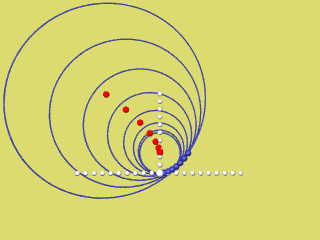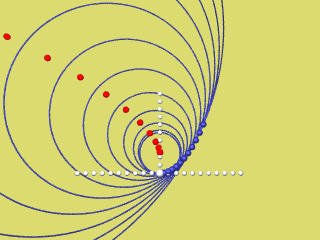
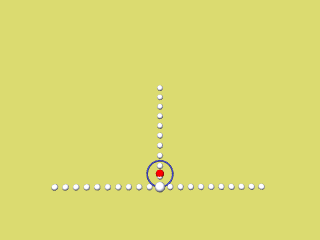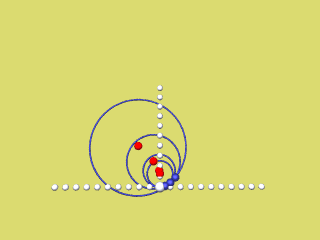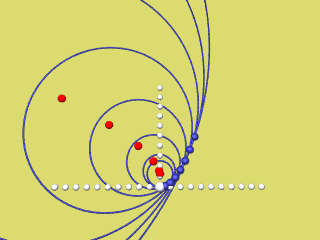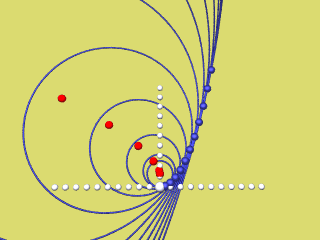
Die nächsten 4 Animationen zeigen für f(x) = a x2 mit a = 0,2 / 0,4 / 0,6 / 0,8 und 1 wie der rechte Parabelast als Hüllkurve der Krümmungskreise entsteht.
Bei Mausklick auf's Bild wird das jeweilige Programmierskript angezeigt.


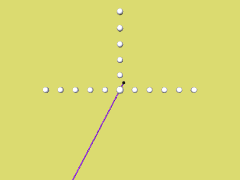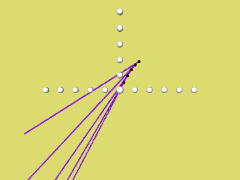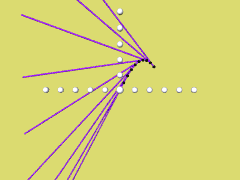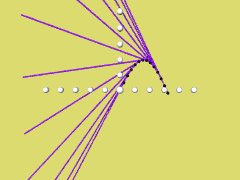
In der folgenden Animation werden für b = 2 die Tangenten
yt = xb cos(a) - ab cos(a) + b sind(a)
gezeichnet, a variiert dabei von 0 bis 3,14. Dabei entsteht als Hüllkurve
y = b sin (x).
| © 2009 Asti | Links für Unterricht | PoVRay-Site |