Grundlegende Rechenschaltungen: Halbaddierer und Volladdierer

1. Halbaddierer
2. Volladdierer
3. Paralleladdierer
4. Subtraktion und Komplementaddition
5. n-Bit-Volladdierer
6. Parallelsubtrahierer
7. Informationsweiche

Der Halbaddierer

Beginnen wir mit der Addition zweier einziffriger Dualzahlen



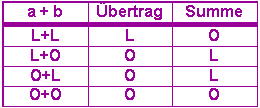
... und sehen uns dann die logischen Terme für Übertrags- und die Summenspalte an:



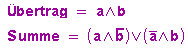
Der Übertrag entspricht also einer AND-Schaltung, die Summe einer ENTWEDER-ODER-Schaltung (Antivalenzschaltung). Es fällt uns also nicht mehr schwer, die zugehörige Schaltung aufzubauen:



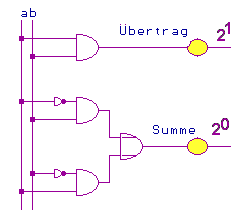
Als abkürzendes Schaltsymbol wird

oder

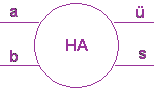
benutzt.

Zusammenfassung: Der Halbaddierer ist eine Schaltung, die 2 einstellige Dualzahlen addieren kann.

• Zum Seitenanfang

Der Volladdierer

Als nächstes sollen zwei mehrstellige Dualzahlen addiert werden:



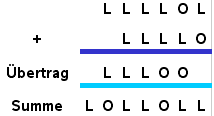
Da dabei ein Übertrag entstehen kann, muss eine Schaltung entwickelt werden, die 3 einstellige Dualzahlen addieren kann.



Wir brauchen also 3 Halbaddierer:

1. Am Eingang des ersten HA's liegen a und b, an seinem Ausgang s_z und ü₁.
2. Am Eingang des zweiten HA'S liegen s_z und c, an seinem Ausgang s (die Einer) und ü₂.
3. Am Eingang des dritten HA's liegen ü1 und ü2, an seinem Ausgang s1 (die Zweier) und die Vierer (die natürlich immer 0 sind).

Insgesamt erhalten wir also die folgenden Schaltung:



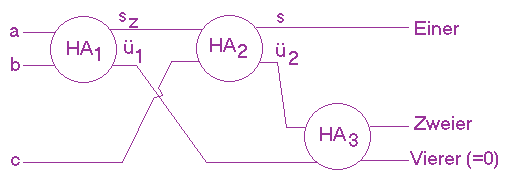
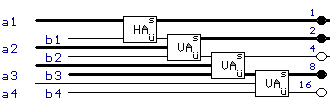
Das abkürzende Symbol ist



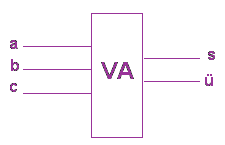
Der Ausgang s entspricht dabei den Einern, der Ausgang ü entspricht den Zweiern. Vierer können nicht auftauchen, da L+L+L drei ergibt.

• Zum Seitenanfang

Der Paralleladdierer

Endlich sind wir soweit, dass wir die Addition von zwei mehrstelligen Dualzahlen angehen können. Dazu sehen wir uns erst nochmals ein Beispiel, dann das allgemeine Additionsschema an:



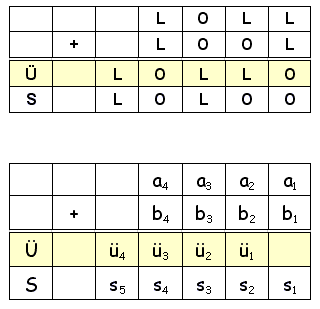
Für die EINER brauchen wir also einen HALBADDIERER, auf dessen Eingängen a₁ und b₁ gelegt werden, an seinem Ausgang liegt dann s₁ und ü₁.
Die ZWEIER werden zum ersten Übertrag addiert und gehen auf den Eingang des ersten VOLLADDIERERS.
Analog geht es dann für den zweiten und dritten Volladdierer weiter. Wir erhalten somit die folgende Schaltung:





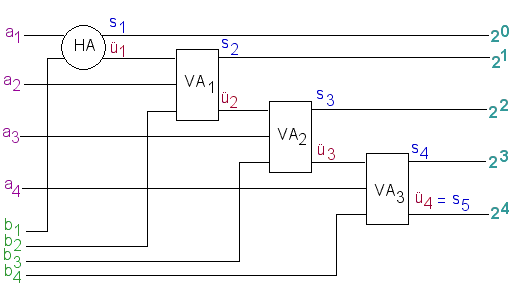
Das folgende Beispiel zeigt die Addition 7+4. An den dick gezeichneten Leitungen liegt Spannung an.

• Zum Seitenanfang

Subtraktion von Dualzahlen

FALL 1: a-b für a>b oder a=b

Wir beginnen mit einem Beispiel:

Was können wir bereits? Addieren und negieren. Versuchen wir also, die Subtraktion darauf zurückzuführen:



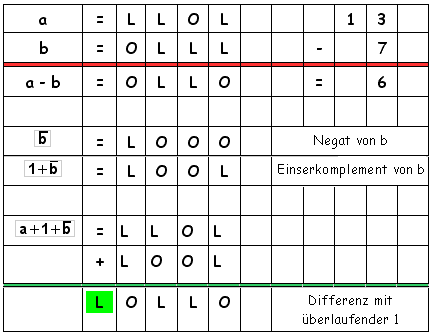
Für unser Beispiel gilt also:

Bilden wir das Negat des Subtrahenden b, addieren 1 zum Negat (Einserkomplement von b), addieren dann das Einserkomplement von b zum Minuend a, dann erhalten wir - von der "überlaufenden 1" abgesehen - das richtige Ergebnis a - b.

Sehen wir uns mal ein beliebiges Beispiel im Dezimalsystem an:
Negat bedeutet hier "Ergänzung auf lauter 9er".



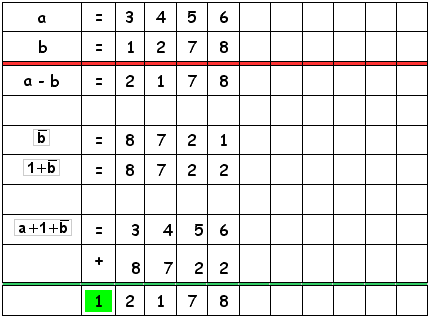
Wieder gilt: Addiert man zum Minuenden a das Einserkomplement des Subtrahenden b, dann erhält man a - b mit einer überlaufenden 1.

Erklärung:


1. Der Merksatz behauptet: a - b = a + NICHT b + 1, abgesehen v.d. überlaufenden 1
   
   Wir dürfen auf beiden Seiten a subtrahieren und erhalten:
   
2. - b = NICHT b + 1 , abgesehen v.d. überlaufenden 1
   
   Wir dürfen auf beiden Seiten b addieren und erhalten:
   
3. 0 = NICHT b + b + 1, abgesehen v.d. überlaufenden 1
   
   
4. Sehen wir uns mal an, was die Summe NICHT b + b ergibt:
   Da NICHT b aus b durch Vertauschung von 0 und L hervorgeht, wird für jeden Stellenwert (EINER, ZWEIER, VIERER, ...) immer die Summe aus 0 und L gebildet, das Ergebnis besteht aus aus lauter L's und hat soviele Stellen wie die "längste" der beiden Dualzahlen a oder b. Überträge kann es nicht geben.



5. Sehen wir uns als nächstes an, was geschieht, wenn zu einer Dualzahl, die nur aus L's besteht, nochmals L addiert wird:
   
   
   
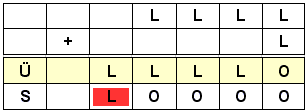
   Es entstehen lauter Nullen und eine überlaufende Eins.
   
   Wenn wir nun eine Schaltung voraussetzen, die die überlaufende Eins "wegmacht", dann haben wir an dieser Stelle das Ergebnis NULL und unsere Behauptung
   0 = NICHT b + b + 1, abgesehen v.d. überlaufenden 1
   ist hiermit bewiesen.

Fall 2: a-b für a<b

Eigentlich sieht doch unsere Erklärung von Fall 1 ganz gut aus. Überprüfen wir sie mal am Beispiel
7 -10 = -3



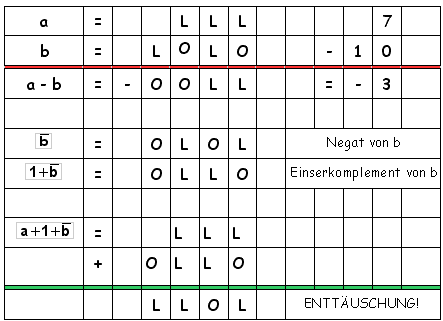
Nein, nix geht. Machen wir einen anderen Versuch: Wir addieren zu a nicht das Komplement von b sondern das Negat von b: Wir erkennen, dass das Ergebnis noch negiert werden muss, auch ein Minuszeichen muss noch dazu!



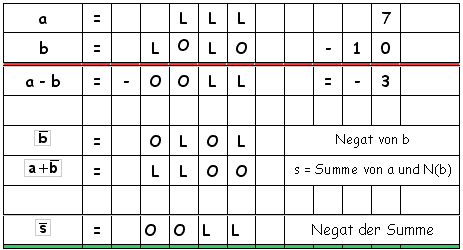
Wir haben für den Fall a<b also eine neue Vorgehensweise demonstriert (deren Beweis man übrigens bei Kreß/Digitale Elektronik umd Computer, Diesterweg, nachlesen kann, hier überlasse ich den Beweis den SchnelldenkerInnen) :

Addiere a zum Negat von b, negiere dann die Summe und setze ein Minuszeichen dazu.

Für die Entwicklung unserer Schaltung sind wir nun ein gutes Stück weiter gekommen: Allerdings müssen wir die Schaltung noch "beauftragen", die Fallunterscheidung selbständig zu erledigen, wir brauchen also eine "Informationsweiche".

Bis später!

• Zum Seitenanfang