Codierer und Decodierer

Anhand der Ziffern 0 bis 9 soll eine Schaltung erarbeitet werden, die Dezimalzahlen (bis 9) in Dualzahlen umwandelt. Zunächst sehen wir uns mal diese Zahlen an:



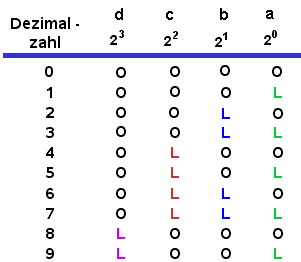
Wir leiten die Codiergleichungen direkt aus der Tabelle ab:

CODIERGLEICHUNGEN:

2⁰ liegt auf L, wenn 1 ODER 2 ODER 5 ODER 7 ODER 9 vorliegt, d.h. L ist.(grün)
2¹ liegt auf L, wenn 2 ODER 3 ODER 6 ODER 7 vorliegt.(blau)
2² liegt auf L, wenn 4 ODER 5 ODER 6 ODER 7 vorliegt.(rot)
2³ liegt auf L, wenn 8 ODER 9 vorliegt.(lila)

Mit Hilfe von ODER-Gattern lässt sich die Codierung Dezimalzahl zu Dualzahl also einfach automatisieren:



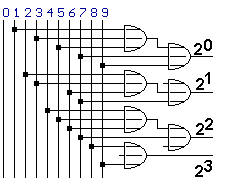
Wegen der Gültigkeit des Assoziativgesetzes darf z.B. ein ODER-Gatter mit 5 Eingängen (für die EINER) durch 2 ODER-Gatter mit 2 bzw. mit 3 Eingängen ersetzt werden!!

Zur Erinnerung: An den Verbindungspunkten der Leitungen muss man sich kleine Schalter denken:




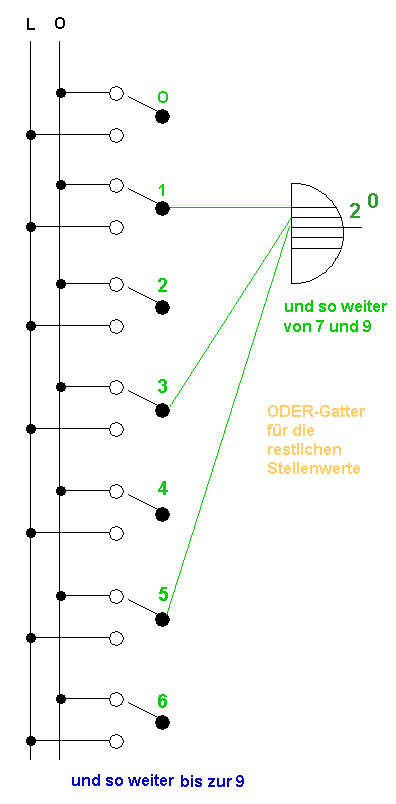
Weiter geht's zur Decodierung Dualzahl zu Dezimalzahl:

Wir sehen uns nochmals unserer Tabelle an:


Da wir bereits Übung darin haben, aus Funktionstabellen logische Terme zu erstellen, leiten wir die Codiergleichungen direkt aus der Tabelle ab:



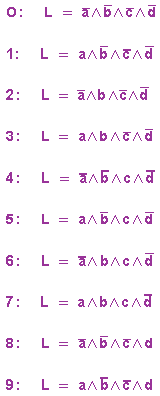
Für die Decodierung ist die Eindeutigkeit der Gleichungen ausreichend, d. h. wir können noch ein bisschen vereinfachen:



und erhalten den Decodierer (Achtung: Negationspunkte vor den Eingängen der UND-Gatter!)



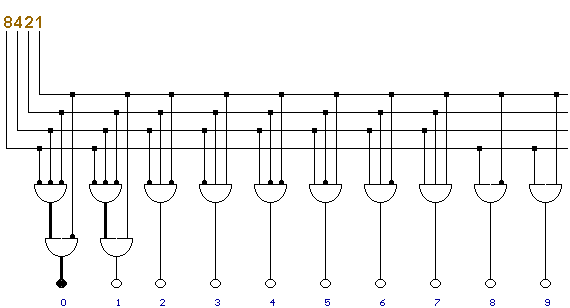
Hier wurde die Ziffer 0 dargestellt: An den Stellenwerten EINER, ZWEIER, VIERER, ACHTER liegt keine Spannung.

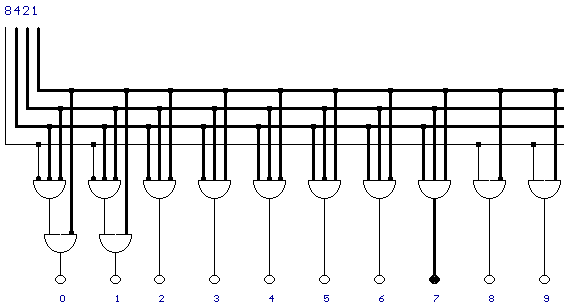
In der nächsten Abbildung wird die 7 dargestellt: 7=4+2+1, an den Stellenwerten VIERER, ZWEIER und EINER liegt also Spannung an:



Für die vielen Stunden des Lötens wurden dann TTL-Schaltkreise verwendet. Hier kannst Du Dich im Internet darüber informieren.

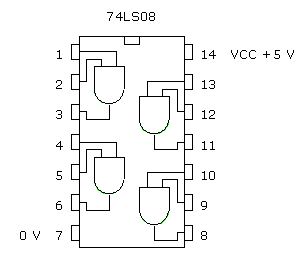
Beispielsweise hat der IC 74LS08 vier AND-Gatter mit je 2 Eingängen:



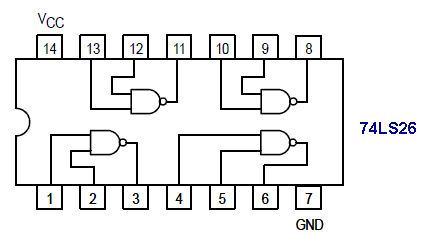
oder ein weiterer Baustein mit 4 NAND-Gattern:



... und hier geht's erst weiter, wenn das Kapitel "Rechenschaltungen" vollständig ist. Bis dann!

• Zum Seitenanfang