Aussagenlogik



Aussagen können mit UND, mit ODER, mit ENTWEDER-ODER, mit WENN-DANN ... verknüpft werden, sie können auch verneint werden. Sehen wir uns das genauer an:

Aussage A: Ich gehe ins Schwimmbad.
Aussage B: Ich spiele Tennis.

Verknüpfung mit UND:
Ich gehe ins Schwimmbad UND ich spiele Tennis.

Verknüpfung mit ODER:
Ich gehe ins Schwimmbad ODER ich spiele Tennis.

Verneinung:
NCIHT A: Es ist nicht wahr, dass ich ins Schwimmbad gehe.
NCIHT B: Es ist nicht wahr, dass ich Tennis spiele.

In allen Fällen kann ich mir überlegen, wann die zusammengesetzte bzw. die verneinte Aussage den Wahrheitswert w(ahr) bzw. f(alsch) hat:
Das Ergebnis wird in einer Wahrheitstafel (Wahrheitstabelle, Funktionstabelle) dargestellt:



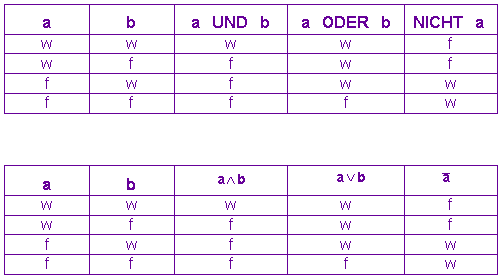
Wir erkennen:

    Eine durch UND zusammengesetzte Aussage ist nur wahr, wenn beide Teilaussagen wahr sind.
    Eine durch ODER zusammengesetzte Aussage ist nur falsch, wenn beide Teilaussagen falsch sind.
    Die verneinte Aussage hat den entgegengesetzten Wahrheitswert der ursprünglichen Aussage.



Sehen wir uns die Wahrheitstafel für WENN A, DANN B an:
Aussage A: Das Wetter ist schön.
Aussage B: Ich gehe schwimmen.
Zusammensetzung: WENN das Wetter schön ist, DANN gehe ich schwimmen.

Offensichtlich kann man mir nur eine Lüge nachweisen, wenn ich trotz schönen Wetters NICHT schwimmen gehe, also nur dann, wenn die erste Teilaussage wahr und die zweite Teilaussage gleichzeitig falsch ist.
Also muss die folgenden Wahrheitstafel gelten:



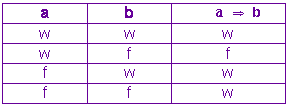
    Eine Implikation ist nur dann falsch, wenn der Vordersatz wahr und der Nachsatz falsch ist.

Zur Implikation passt natürlich gut die ÄQUIVALENZ: WENN A, DANN B und gleichzeitig WENN B, DANN A. A und B sollen also einander äquivalent sein. Aus dieser Forderung folgt sofort die Wahrheitstabelle, sie enthält für die zusammengesetzte Aussage genau dann ein w, wenn A und B den gleichen Wahrheitswert haben:



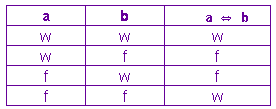
    Eine Aquivalenz ist genau dann wahr, wenn der Vordersatz und der Nachsatz den gleichen Wahrheitswert haben.

Verneint man die Aquivalenz (es ist nicht wahr, dass A äquivalent zu b ist), dann erhält man die sog. ANTIVALENZ (ENTWEDER A ODER B). Die Wahrheitstafel muss die entgegengesetzten Werte wie die Aquivalenz enthalten:



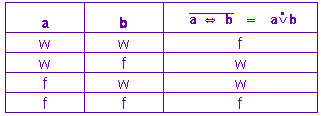
    Eine Antivalenz ist genau dann wahr, wenn der Vordersatz und der Nachsatz verschiedene Wahrheitswerte haben.
Allen bisher genannten Verknüpfungen von Aussagen entsprechen elektronische Schaltungen. Darüber kannst Du dann im nächsten Kapitel nachlesen.





© 2010 Asti PoVRay-Site Mathematische Streiflichter