Dualzahlen (Binärzahlen, Zweiersystem)


Zunächst mal die Info zum Aufbau einer Dualzahl:

Unser Dezimalsystem hat die Stellenwerte Einer, Zehner, Hunderter, ... Jede Zahl läßt sich als Vielfaches dieser Zehnerpotenzen darstellen:

256 = 2 • 100 + 5 • 10 + 6 • 1
= 2 • 102 + 5 • 101 + 6• 100


Ganz genauso funktioniert das Zweiersystem: die Stellenwerte sind hier die Potenzen der Zahl 2. Die Ziffern werden mit L und 0 bezeichnet, um eine Verwechslung mit 1 und 0 auszuschließen:

L0L = L • 4 + 0 • 2 + L• 1
= L • 22 + 0 • 21 + L • 20


Die Dualzahl L0L ergibt also die Dezimalzahl 4+0+1=5.


Auch über das Dividieren durch Zehner- bzw. Zweierpotenzen solltest du informiert sein:

Dividiert man eine Dezimalzahl durch 10, das Ergebnis wieder durch 10 usw., dann ergeben die Divisionsreste die Zahl rückwärts, d.h. beginnend mit Einern, dann Zehnern, ... :



Erklärung:

Um die Reste zu sehen kann man das auch wie folgt darstellen:
256 = [2•100 + 5•10] + 6
=[(2•10 + 5)•10] + 6


Dividiert man nun eine Dezimalzahl durch 2, das Ergebnis wieder durch 2, ... so erhält man die binäre Darstellung dieser Zahl beginnend mit 20, 21, 22, ...

Führe dies mal am Beispiel 84 durch, dein Ergebnis ist dann: 84 = L0L0L00

Dieser Sachverhalt ist gut verwendbar, wenn man ein Programm (in welcher Programmiersprache auch immer) schreiben will, das Dualzahlen aus Dezimalzahlen erzeugt.




Genauso wie das Binärsystem funktionieren auch alle anderen Zahlensystem: Im Hexedezimalsystem wird die Zahl 16 als Basis benutzt, im Oktalsystem die Zahl 8,....



Rechnen mit Dualzahlen: Addition und Subtraktion



Sehen wir uns eine Addition genauer an (29+7=36):



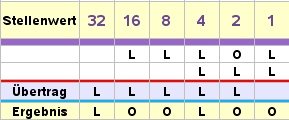
  1. Die Addition der beiden EINER ergibt einen ZWEIER, der als Übertrag notiert wird. O EINER werden beim Ergebnis notiert.
  2. Die Addition der beiden ZWEIER ergibt einen VIERER, der als Übertrag notiert wird. O ZWEIER werden beim Ergebnis notiert.
  3. Dei Addition der drei VIERER ergibt einen VIERER, der ins Ergebnis geschrieben wird, und einen ACHTER, der als Übertrag notiert wird.
  4. Die beiden ACHTER ergeben dann O ACHTER im Ergebnis und einen ACHTER im Übertrag.
  5. Genauso ist's bei den SECHZEHNERN: "O hin und eins im Sinn". Und so landet dann ein ZWEIUNDDREISSIGER im Endergebnis.


Nicht anders führt man die Addition von mehreren Dualzahlen durch. Auch die Subtraktion läuft genauso über's "Ergänzen", wie uns aus dem Dezimalsystem bekannt ist:



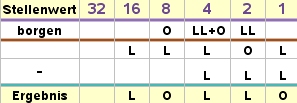
  1. Kein Problem bei den EINERN: L + O = L
  2. Wir borgen einen VIERER und verwandeln ihn in 2 ZWEIER: L + L = zweimal L
  3. Wir haben keine Vierer mehr und verwandenl einen ACHTER in 2 VIERER: L + L = zweimal L
  4. Für die ACHTER gilt dann: O + O = O
  5. Für die SECHZEHNER gilt: O + L = L


KOMMAZAHLEN im Binärsystem


Auch hier läuft's nicht anders als bei den Dezimalzahlen: Wir sehen uns einfach mal die Stellenwerte in beiden Systemen an:



In unserem Dezimalsystem sind die Stellenwerte nach dem Komma also ein Zehntel, ein Hundertstel, ....(Zehnerpotenzen mit negativen Hochzahlen), im Binärsystem entsprechen sie ebenfalls den Zweierpotenzen mit negativen Hochzahlen, nämlich ein Halb, ein Viertel, ein Achtel, ....

Divisionen, die Kommazahlen ergeben:

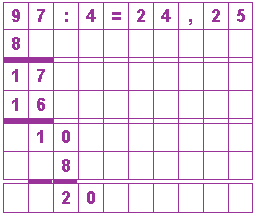
Zur Erinnerung das schriftliche Dividieren im Dezimalsystem:
Die neun Zehner werden durch 4 geteilt und man erhält 2 Zehner als Ergebnis, einer bleibt übrig, der zusammen mit den Einern 17 ergibt. Diese siebzehn Einer werden ebenfalls durch 4 geteitl und man erhält 4 Einer, ein Einer bleibt übrig. Dieser wird in Zehntel verwandelt (beim Ergebnis wird daher jetzt das Komma gesetzt), man hat also 10 Zehntel, die nun durch 4 geteilt werden. Dies ergibt 2 Zehntel und 2 Zehntel bleiben übrig, die nun in 20 Hundertstel verwandelt werden. Diese werden wiederum durch vier geteilt und man erhält 5 Hundertstel als Ergebnis.



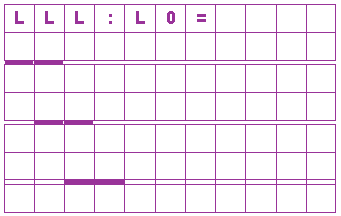
Dividiere nun im Binärsystem LLL durch L0 unter Benutzung des obigen Rechenschemas: (Durch Umrechnung in Dezimalzahlen kannst Du dann Dein Ergebnis selbst kontrollieren.)



Nun noch 2 Umrechnungen:



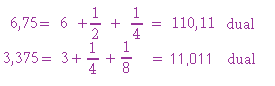
    Und nun die Preisfrage für SchnelldenkerInnen:

    Wandelt man im Dezimalsystem (gekürzte) Brüche in Kommazahlen um, so muss man dividieren. Man erhält dann abbrechende, sofortperiodische und nichtsofortperiodisch Kommazahlen.

    Woran liegt das? Ganz einfach: Wir sehen uns die Nenner und deren Primzahlzerlegung an:



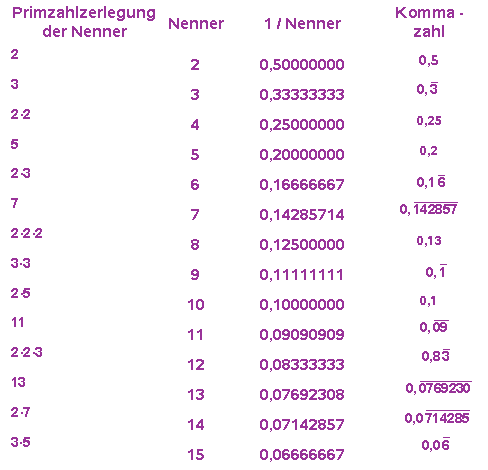
    Wir erkennen: Enthält der Nenner des gekürzten Bruches nur die Zahlen 2 und/oder 5 als Primfaktoren, dann erhalten wir eine abbrechende Kommazahl.
    Enthält der Nenner des gekürzten Bruches eine Mischung aus den Zahlen 2 und/oder 5 und anderen Zahlen als Primfaktoren, dann erhalten wir eine nichtsofortperiodische Kommazahl.
    Enthält der Nenner des gekürzten Bruches nur andere Zahlen als die Zahlen 2 und/oder 5 als Primfaktoren, dann erhalten wir eine sofortperiodische Kommazahl.

    Und hier nun die PREISFRAGE: Welche Dezimalbrüche ergeben abbrechende, nichtsofortperiodische bzw. sofortperiodische Kommazahlen im Binärsystem?










© 2010 Asti PoVRay-Site Mathematische Streiflichter