AND (UND), OR (ODER) und NICHT-Schaltung



UND-, ODER- und NICHT-Schaltungen bilden die Grundlagen für sämtliche Rechenschaltungen (z.B. Halbaddierer, Volladdierer, Parallelsubtrahierer, Schieberegister, JK-Master-Slave-FlipFlop, ...)



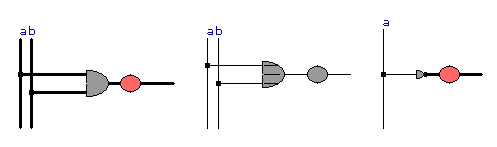
    Erklärung:

    Bedeutung der senkrechten Linien: Wird der Eingang z. B. eines UND-Gatters auf L gelegt, so muss er mit einer Spannungsquelle verbunden werden, die durch die senkrechte Linie dargestellt wird. Stellt man sich an den Verbindungsstellen Schalter vor, so können die Eingänge der UND- und ODER-Gatter beliebig mit O Volt oder 5 Volt verbunden werden.

    Im Internet kannst Du hier Bausteine eines Demosystems sehen.

Bei der neueren DIN-Norm werden die ff. Symbole benutzt:



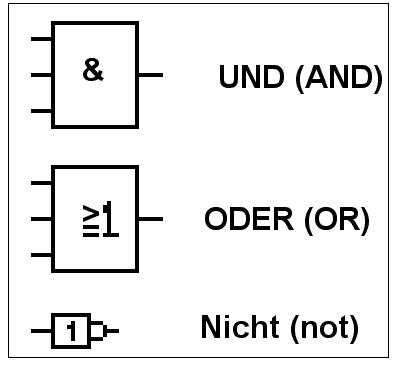
Die UND-Schaltung entspricht der Reihenschaltung zweier Schalter, die ODER-Schaltung der Parallelschaltung zweier Schalter, die NICHT-Schaltung ist ein Relais.

In der Praxis werden natürlich keine mechanischen Schaltelemente benutzt, sondern Halbleiterbausteine (siehe Schaltfläche oben).

UND, ODER und NICHT bestehen aus Transistoren - Genaueres darüber dann später.

RELAIS Die "mechanische" NICHT-Schaltung ist das Relais.



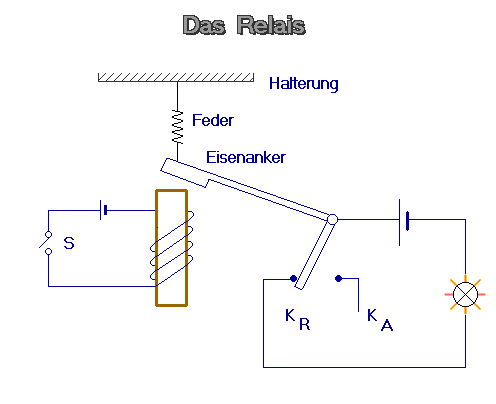
Ist der linke Stromkreis von Strom durchflossen, dann zieht der Eisenkern der Spule den Anker an, und der rechte Stromkreis wird geöffnet.



Im Internet findest Du bei Kazuhiko Arase ein Applet, mit dem Du eigene logische Schaltungen ausprobieren kannst.



AND- OR- und NICHT-Gatter können auf vielfältige Weise zusammengeschaltet werden. Dazu sollen nun einige Beispiele folgen.

Beispiele
  1. Die Äquivalenzschaltung

    Sehen wir uns nochmals ihre Wahrheitstabelle an:



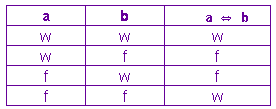
    Nur in der ersten Zeile (a und b sind beide wahr) und in der vierten Zeile (a und b sind beide falsch, bzw. nicht a und nicht b sind beide wahr) hat sie den Wahrheitswert wahr, was also auch für den folgenden logischen Term gelten muss:





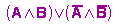
    In der Schaltalgebra werden statt der Wahrheitswerte w und f die Zeichen L und 0 benutzt: Nur dann, wenn an a und b Spannung anliegt, liegt auch am Ausgang der Schaltung Spannung an und eine dort geschaltete Leuchtdiode leuchtet. Wirklich verständlich wird dies erst dann, wenn man sich ansieht, wie die logischen Gatter aus Transistoren aufgebaut sind.

    Für "es liegt Spannung an" schreibt man L, für "es liegt keine Spannung an" schreibt man 0 und erhält also die folgende Funktionstabelle für die Äquivalenzschaltung:



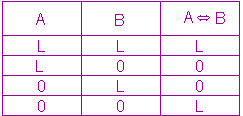
    Anhand des logischen Terms der Äquivalenzschaltung erkennt man, dass A und B mit einem UND-Gatter verbunden werden müssen, außerdem müssen A und B beide einzeln negiert werden, danach ebenfalls mit einem UND-Gatter verbunden werden. Die Ausgänge der beiden UND-Gatter werden dann durch ein ODER-Gatter verbunden. Wir erhalten die Äquivalenzschaltung:



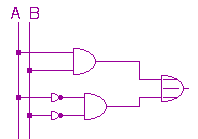
    Mit dem Applet von Kazuhiko Arase oder mit dem Programm LOCAD3 kannst Du die Funktionstabelle überprüfen.

    In der ff. Abbildung symbolisieren die dick gezeichneten Leitungen anliegende Spannung und man erkennt, dass nur in der 1. und 4. Zeile der Tabelle die Leuchtdiode Spannung hat.:



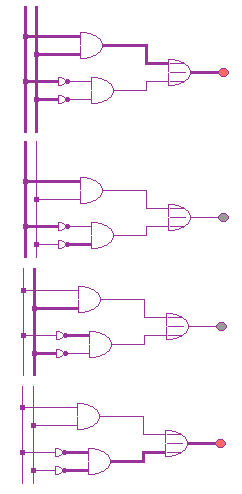
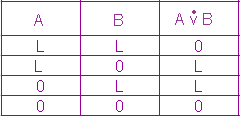
  2. Die Antivalenzschaltung

    Diesmal starten wir mit einer logischen Schaltung, schalten sie dann mit LOCAD3 ein und zeigen auf diese Weise, dass ihre Funktionstabelle der Antivalenz entspricht.

    Wir verbinden NICHT A und B mit den Eingängen eines UND-Gatters, ebenso verbinden wir A und NICHT B mit den Eingängen eines UND-Gatters. Die Ausgänge der beiden UND-Gatter werden dann auf ein ODER-Gatter gelegt. An diesem Text ist auch schon erkennbar, dass wir die Funktionstabelle der Antivalenzschaltung "nachgebaut" haben.




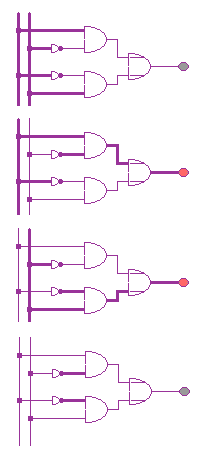
    Nur in der 2. und 3. Zeile leuchtet die Leuchtdiode.


... und wer ein bisschen üben will, kann sich das erste Aufgabenblatt im PDF-Format ausdrucken.








© 2010 Asti PoVRay-Site Mathematische Streiflichter