Schwingkreis - für SchülerInnen in Abiturnähe

Elektrische Schwingungen treten bei der Entladung jedes Kondensators über eine Leitung mit Selbstinduktion auf, wenn der Ohmsche Widerstand einen bestimmten Wert, der durch C und L gegeben ist, nicht überschreitet.

Ein elektrischer Schwingkreis besteht aus einer Spule mit der Selbstinduktion L (Quotient aus Spannungsstoß und Stromänderung),



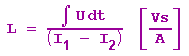
einem Kondensator mit der Kapazität C und einem Ohmschen Widerstand R, die in Reihe geschaltet sind.

1. Ungedämpfte freie elektrische Schwingungen
   
   Betrachten wir zunächst einen Schwingkreis aus C und L mit einem so kleinen Ohmschen Widerstand, dass die Entwicklung Joulescher Wärme im Schwingkreis vernachlässigt werden kann. Wenn dem System dann keine elektrische und magnetische Energie entzogen wird, gilt nach dem Energieerhaltungssatz, dass die Summe aus der elektrischen Energie des Kondensators und der magnetischen Energie der Spule bei den wechselnden Entladungen konstant bleibt:
   
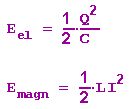   Also gilt nach dem Energieerhaltungssatz:
   
   
   
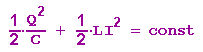
   Der durch die Spule fließende Strom ergibt sich durch Differentiation nach der Zeit:
   
   
   
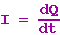
   Man erhält also (Kettenregel beim Differenzieren beachten!)
   
   (*)
   
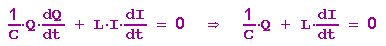   Nochmaliges Differenzieren ergibt dann
   
   (**)
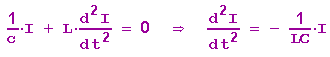   Diese Gleichung hat die Form der Bewegungsgleichung des ungedämpften elektrischen Pendels, eine Lösung ist
   
   
   
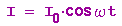
   Zur Lösung einfacher Differentialgleichungen siehe HIER
   
   Es gilt dann die Thomsonsche Schwingungsformel
   
   
   
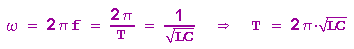
   Die beiden Kondensatorplatten sind über die Spule miteinander verbunden. Durch den Entladestrom wird in der Spule eine Spannung induziert, die der Kondensatorspannung gleich aber entgegengesetzt gerichtet ist:
   
   
   
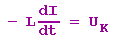
   Ist die Kondensatorspannung Null, so muss auch die Änderungsgeschwindigkeit der Stromstärke Null sein, d. h. die Stromstärke hat dann ihren Maximalwert erreicht, es ergibt sich also eine Phasenverschiebung um , um die der Stom hinter der Spannung zurück bleibt.
   
   
   
2. Gedämpfte freie elektrische Schwingungen
   
   Tatsächlich jedoch hat der aus C und L gebildete Schwingkreis einen Ohmschen Widerstand, der zur Entwicklung Joulescher Wärme führt. Die Abnahme elektrischer und magnetischer Energie entspricht dann der pro Zeiteinheit erzeugten Wärme:
   
   
   
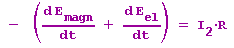
   Setzt man (*) in diese Gleichung ein, dann erhält man:
   
   
   
   Diese Gleichung wird durch I dividiert und anschließend differenziert:
   
   
   
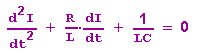
   Dies ist die Form der Bewegungsgleichung der gedämpften elektrischen Schwingung. Diese Gleichung tritt nun an die Stelle von (**), in die sie für R=0 übergeht.
   
   Der Lösungsansatz
   
   
   
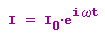
   führt zu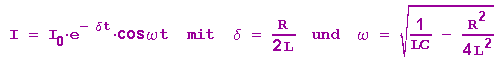
   
   woraus die Thomsonsche Schwingungsformel folgt:
   
   
   
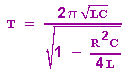
   Die Amplitude
   
   
   
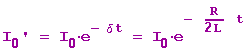
   nimmt also mit einer Exponentialfunktion ab.
   Die Größe
   
   
   
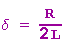
   heißt Dämpfungsfaktor.
   Das Verhältnis zweier mit der Schwingungsdauer T aufeinanderfolgender maximaler Stromwerte ist
   
   
   
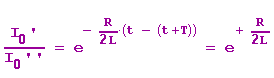
   Der natürliche Logarithmus dieses Verhältnisses heißt logarithmisches Dekrement und ist für einen gegebenen Schwingkreis konstant:
   
   
   
   
   
   
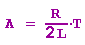
3. Erzwungene elektrische Schwingungen
   
   Zu ihrer Erzeugung wird der Schwingkreis mit einer äußeren Wechselspannung erregt. Die aufgeprägte Spannung ist dann gleich der Summe der Einzelspannungen.
   
   Genaueres können Interessierte dann in 'Gerthsen, Physik' nachlesen.



4. Gekoppelte elektrische Schwingungen
   
   Zwie Systeme, die in irgend einer Weise so verbunden sind, dass sie eine Rückwirkung aufeinander ausüben, heißen gekoppelt.
   Im Gegensatz zu den erzwungenen elektrischen Schwingungen ist hier der Energievorrat des System nicht unendlich groß, sondern begrenzt.
   
   Man unterscheidet verschiedene Kopplungsarten:
   
   
   
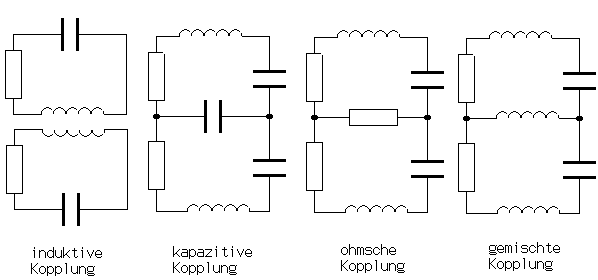
   Und wen's interessiert, der liest weiter bei 'Gerthsen'.



5. Schwebungen
   
   erhält man bei Überlagerung zweier harmonischer Schwingungen, deren Frequenzen sich nur leicht voneinander unterscheiden:
   
   Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and active in your browser (Click here to install Java now)
   
   Im Applet erkennt man: Je weniger die Frequenzen der Einzelschwingungen voneinander abweichen, desto geringer ist die Zahl der Schwebungen.
   Die Amplitude der Schwebung geht nur dann auf Null herunter, wenn die Amplituden der Einzelschwingungen gleich sind.
   Weiteres: Siehe 'Gerthsen'.
   



6. Lissajous-Ellipsen
   
   Zwei senkrecht zueinander erfolgende Schwingungen gleicher Frequenz aber verschiedener Amplitude
   
   x=x_o sin (wt) und y=y_o sin (wt+p)
   
   ergeben i.a. eine elliptische Schwingung, die unter besonderen Umständen (phi=0,pi,..) in eine geradlinige Schwingung ausartet. Mit der Phasendifferenz ändert sich sowohl die Richtung der großen Achse als auch das Achsenverhältnis der Ellipse.
   
   Links:
   Im Netz aller Netze finder ihr HIER ein Applet zu Lissajous-Figuren.
   Es gibt auch ein Delphi-Programm LISSAJOUS