- WPU Jahrg. 10
- Abstimmanlage
- FlipFlop
- DL und DTL
- RTL und RCTL
- Radio - Geschichte
- Radio 2
- Lausprecherweiche
- Radio 3
- Transformator
- Modulation
- Detektorempfänger
- Arbeitspkt Transistor
- Radio 4
- Thyristor
- Literaturverzeichnis
- Start HL-Elektronik
- Startseite
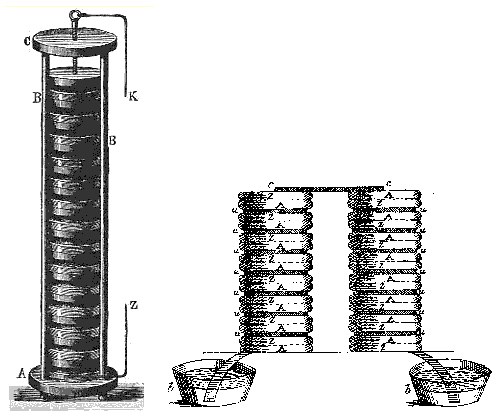
Voltaelement
Luigi Galvani, Professor der Medizin an der Universität$t von Bologna,
machte im Jahr 1789 eine merkwürdige Beobachtung:
Er studierte die Nerven von Fröschen, indem er bei den getöteten Tieren
die Beinnerven freilegte. Berührte er mit einem Ende den Beinnerv und mit
dem anderen das Froschbein selbst, so zuckte es heftig zusammen.
Das geschah nur, wenn der Draht aus zwei verschiedenen Metallen bestand.
Alessandro Volta (1745 - 1827), Professor der Physik in Padua, hörte
davon und begann zu experimentieren. In einem Brief schreibt er:
Ich verschaffte mir einige Dutzend kleiner runder Scheiben aus Kupfer,
Messing oder Silber, einen Zoll oder mehr im Durchmesser und eine gleiche
Anzahl Zinkplatten. Ich verfertigte außerdem eine genügende Anzahl
runder Scheiben aus Pappe, Leder oder anderem porösen Material, welches
fähig ist, viel Feuchtigkeit oder Wasser aufzunehmen. ... Ich lege auf
einen Tisch eine der metallischen Platten, z. B. Silber ... und auf die-
se lege ich eine von Zink. Hierauf kommt eine der feuchten Platten,darauf
eine zweite Silberplatte usw... In gleicher Weise fahre ich fort,
eine so hohe Säule zu bauen, dass ich sie halten kann, ohne umzufallen.
Die Entwicklung der Voltasäule ist einer der größten Fortschritte in
Physik und Technik: Sie ermöglichte erstmals, einen elektrischen Strom
über längere Zeit zu erzeugen und seine Wirkungen zu beobachten.
Vor Volta konnte man nur kurze Entladungen erzeugen.
Hier ein Link ins Internet zum Thema 'Batterien'.
Elektrischer Strom und Magnetfeld
Wird ein elektrischer Leiter von Strom durchflossen, dann stellen sich drehbar gelagerte Kompassnadeln in konzentrischen Kreisen um den Leiter ein: Der stromdurchflossene Leiter hat also ein Magnetfeld aufgebaut.
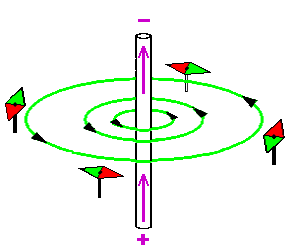
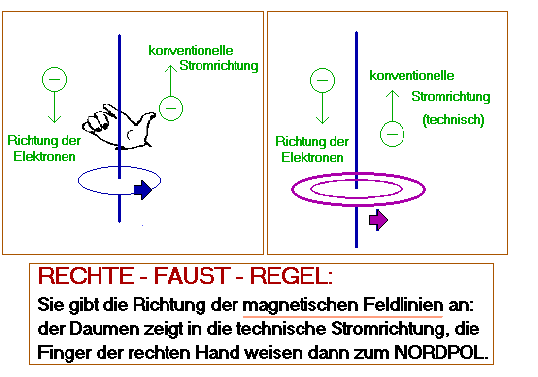
Für die Richtung der magnetischen Feldlinien gilt die rechte-Faust-Regel :
Elektromagnetische Wellen
Magnetische und elektrische Feldstärke stehen senkrecht aufeinander und schwingen senkrecht zur Ausbreitungsrichtung:
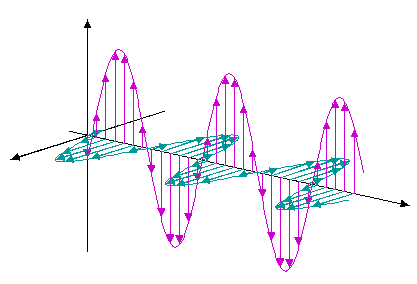
Ein Applet zur Ausbreitung elektromagnetischer Wellen findet Ihr hier auf dem Landesbildungsserver von BW.
Auch beim LBS/BW hier ein Überblick zum Thema.
Tiefpass
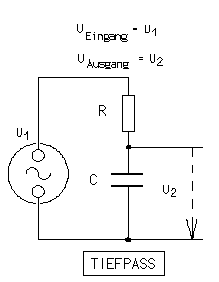
Ein Tiefpass ist eine Spannungsteilerschaltung, die tiefe Wechselspannungsfrequenzen und Gleichspannung ungehindert durchlässt und hohe Frequenzen abschwächt und eine Phasenverschiebung bewirkt.
Im Vergleich zum Hochpass sind R und C vertauscht.
Für das Spannungsteilerverhältnis ergibt sich:
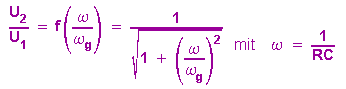
Hochpass
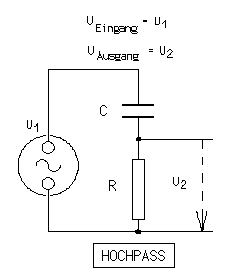
Der sog. Hochpass ist ein frequenzabhängiger Spannungsteiler, der hohe Frequenzen bevorzugt.
Er hat die folgende Ausgangsspannung: (Genaueres siehe hier und hier)
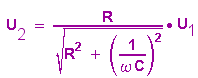
An der obigen Gleichung erkennt man, dass der Quotient U2:U1 für hohe Frequenzen gegen 1 strebt. Bei niedrigen Frequenzen wird der Nenner sehr groß, der Quotient strebt gegen 0, was die ff. Grafik zeigt.
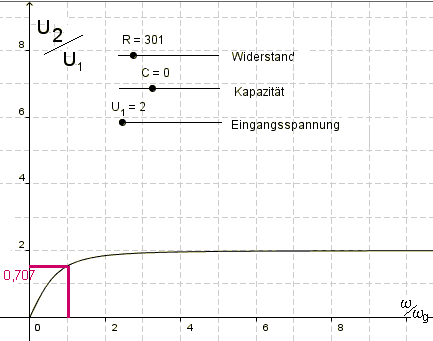
I.a. wird auf der waagrechten Achse eine logarithmische Skala verwendet. (Geogebra weigert sich)
Hier noch ein Link ins Netz aller Netze. Die niedrigen Frequenzen werden also weggesiebt. Durch Einführen einer Grenzfrequenz
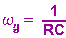
erhält man das Spannungsteilerverhältnis
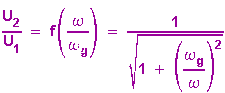
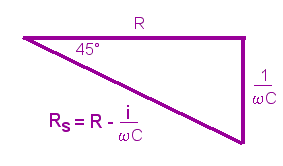
Das Zeigerdiagramm ist:
Zeigerdarstellung sinusförmiger Wechselgrößen
Bei der Zusammensetzung zweier frequenzgleicher sinusförmiger phasenverschobener Wechselströme wählt man den Nullpunkt so, dass ein Nullphasenwinkel verschwindet:
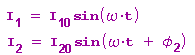
Jedem Strom kann man dann einen Drehzeiger zuordnen:
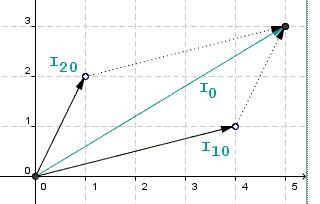
Durch Addition der Momentanwerte und ein bisschen Rechnerei kann man zeigen, dass sich mehrere Sinusströme gleicher Frequenz trotz ihrer gegenseitigen Phasenverschiebung und ihrer unterschiedlichen Scheitelwerte wieder zu einem Sinusstrom zusammensetzen. Scheitel- und Effektivwerte sind dabei vektoriell, Momentanwerte algebraisch zu addieren.
Anstelle vieler Formeln hier einfach ein Applet zum selber ausprobieren. Man erkennt dann, dass die Summe der beiden schwarz gezeichneten Sinusfunktionen wieder eine Sinusfunktion ergibt.:
Stromkreis mit Kondensator:
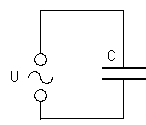
Es sei
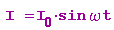
Am Kondenator wird dann die Gegenspannung
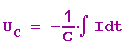
aufgebaut. Da nach den Kirchhoff'schen Gesetzen die Summe der Spannungen Null ergeben muss, gilt:
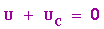
Also
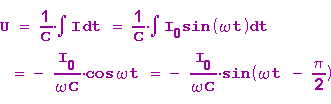
d. h. die Klemmenspannung ist wie der von ihr erzeugte Strom sinusförmig und eilt diesem um pi-halbe nach.
Der Quotient aus Spannung und Strom ist der kapazitive Widerstand
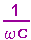
Die am Kondesator aufgebaute Spannung eilt dem Strom um pi-halbe voraus, sie liegt also mit der Klemmenspannung in Gegenphase.
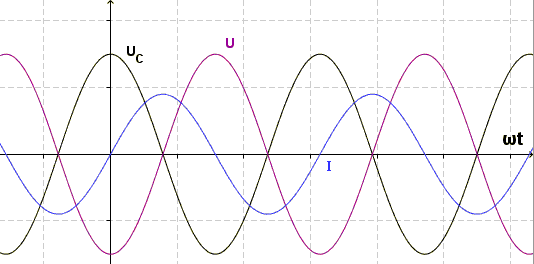
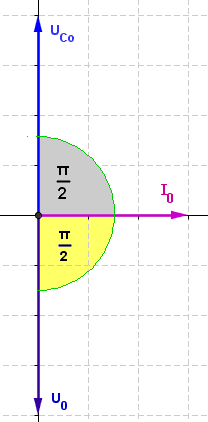
Zeigerdiagramm für den kapazitiv belasteten Stromkreis:
Stromkreis mit Widerstand und Kondensator:
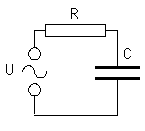
Es ist
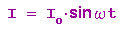
Die mit den Momentanwerten gebildete Spannungsgleichung wird dann zu:
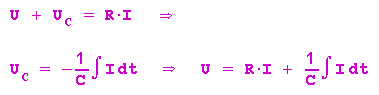
Die Klemmenspannung ist also in jedem Augenblick aus 2 Teilen zusammengesetzt, nämlich dem Ohmschen Spannungsabfall und dem kapazitiven Spannungsverbrauch, der in Gegenphase zur Kondensatorspannung liegt und dieser an Größe gleich ist.
Mit
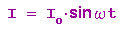
gilt dann also:
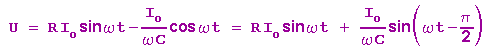
Beide Spannungsanteile sind sinusförmig. Ihre Scheitelwerte sind

Zeigerdiagramam für den Kreis mit R und C:
Der ohmsche Spannungsabfall ist phasengleich mit dem Strom, der kapazitive Spannungsverbrauch eilt ihm um pi-halbe nach. Den Scheitelwert Uo der Klemmenspannung erhält man dann durch (geometrische) Summenbildung der beiden:
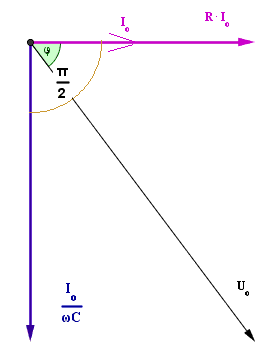
Aus dem Spannungsdreieck
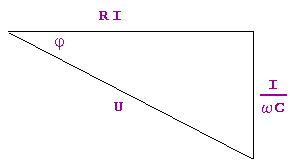
folgt:
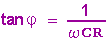
Es ist also
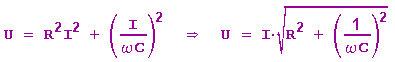
Der Scheinwiderstand ist dann
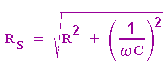
| © 2010 Asti | PoVRay-Site | Mathematische Streiflichter |