Einfache Typen von Differentialgleichungen und ihre Lösungen

A POTENZFUNKTIONEN

Die folgende Abbildung zeigt für verschiedene reelle Exponenten die Potenzfunktion y=axⁿ mit a= 1,5.



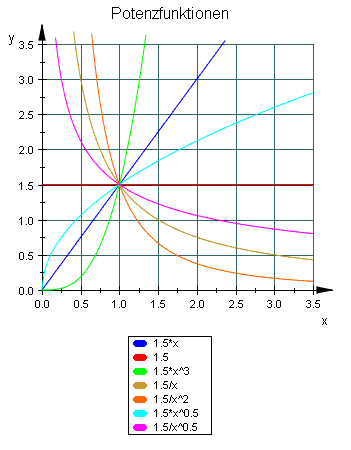
Für die Ableitung gilt dann: y'=anx^n-1.

Bildet man nun den Quotienten aus Funktion und zugehöriger Ableitung, dann erkennt man dessen Proportionalität zu x und hat gleichzeitig diejenige Differentialgleichung, die als Lösung die zugeh. Potenzfunktion hat:



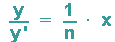
Geometrische Interpretation:

Sonderfälle von POTENZFUNKTIONEN

FALL 1: Quadratwurzel respektive Parabel:

Leitet man die Funktion ab und bildet dann das Produkt y y', so erkennt man, dass die Subnormale eine konstante Länge hat.



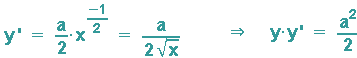
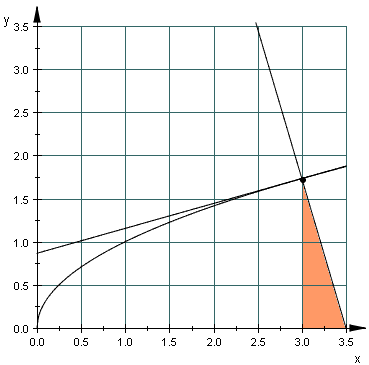
In den ff. vier Abbildungen wurde



dargestellt. Man erkennt die konstante Länge der Subnormale (jeweils 0,5 Längeneinheiten in den 4 Beispielen) sowie die Tatsache, dass
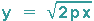
mit der Differentialgleichung y y' = p verbunden ist.









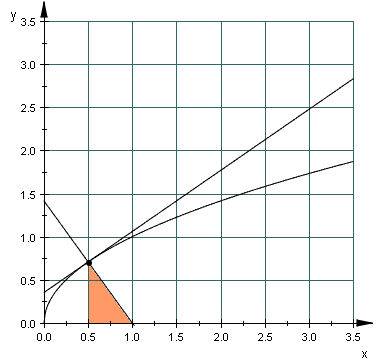
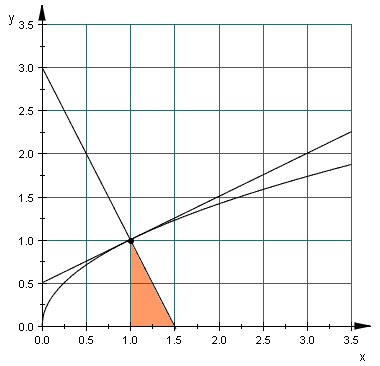
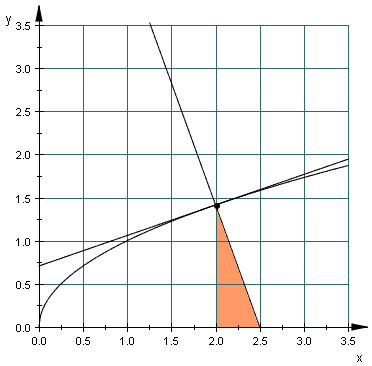
Zur Erinnerung:

Siehe auch hier

FALL 2: Die Potenzfunktion y=axⁿ mit a ungleich 0 und n reell und Polynome n-ten Grades mit von Null verschiedenen Koeffizienten

Für y=axⁿ gilt:



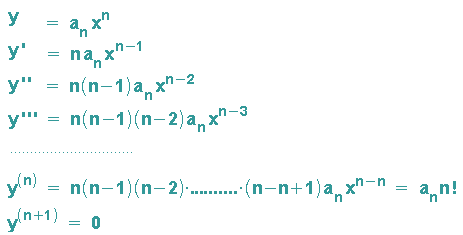
Die n-te Abletiung ist also konstant, die (n+1)-te Ableitung wird Null.

Auch für Polynome n-ten Grades, deren übrige Koeffizienten von Null verschieden sind, gilt diese Aussage:



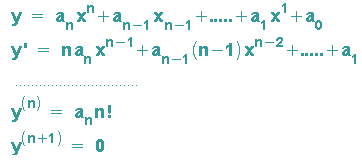
Also hat die DGL y ⁽ⁿ⁾ = a _n n! = const als Lösung das Polynom n-ten Grades



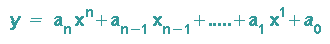
Dies kann noch verallgemeinert werden:



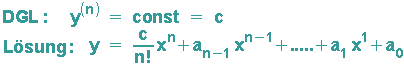
Zur Festlegung der Integrationskonstanten dienen Anfangsbedingungen (an einer einzigen Stelle der unabhängigen Variablen hat man Kenntnis über die gesuchte Funktion und ihre Ableitungen) oder Randbedingungen (für verschiedenen Werte der unabhängigen Variablen gibt es vorgeschriebene Bedingungen).
Vgl. z. B. "Freier Fall": Anfangsbedingungen sind gegeben.

B SINUS und KOSINUS

Zur Sinus- und Kosinusfunktion gehört also die DGL y''=-y.

Verallgemeinerung:

Die DGL y''+ c²y = 0 hat die Lösung y = a sin cx + b cos cx.

C EXPONENTIALFUNKTIONEN

1. Die e-Funktion:

y = c e ^bx hat die Ableitung y = cb e ^bx = by, die also zur Ausgangsfunktion proportional ist.

Bildet man den Quotienten aus Funktion und Ableitung, so erhält man:



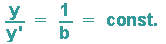
2. Die allgemeine Exponentialfunktion:

y = c a ^bx hat die Ableitung y = cb a ^bx ln a = b ln a y, die also wieder zur Ausgangsfunktion proportional ist.
Bildet man den Quotienten aus Funktion und Ableitung, so erhält man:



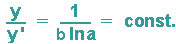
Als Charakteristikum für Exponentialfunktionen erhält man somit eine konstante Subtangente:







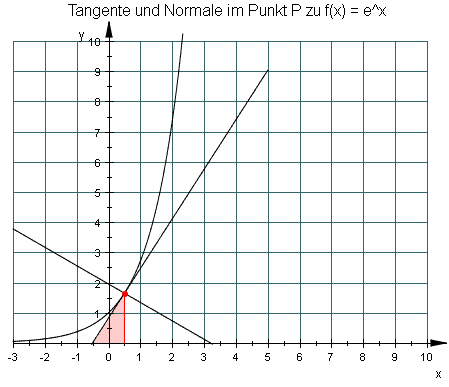
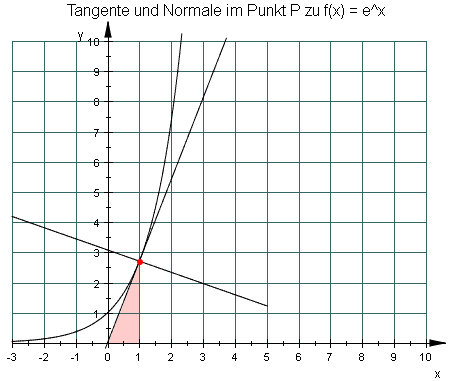
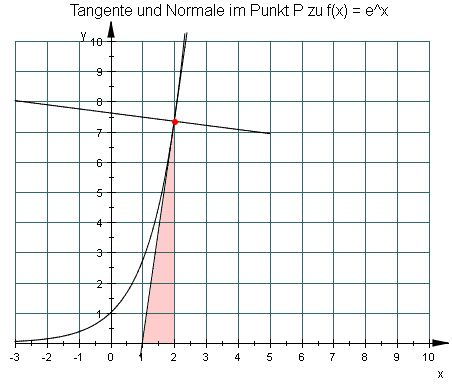
Bemerkung:

In Biologie, Medizin, Physik, ... findet man häufig das Gesetz des organischen Wachstums:
Die Proportionalität y'=ky in Verbindung mit der unabhängigen Variablen Zeit t besagt, dass die Wachstumsgeschwindigkeit (Änderungsgeschwindigkeit) y' zur Größe y selbst proportional ist (Bakterienkultur, Algenwachstum, Tierpopulation, radioaktiver Zerfall mit negativem k, ...).

dy = ky dt kann daher als Differentialgleichung des organischen Wachstums bezeichnet werden. Ihre Lösung ist y=b e ^kx .

D LOGARITHMUS

Es gilt:


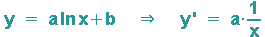
d. h. die DGL



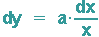
hat die Lösung

Quellenangaben: Prof. Dr. Walther / R. Heinze: Vorlesungsskript über DGL
Vgl. auch die Linkseite.