- WPU Jahrg. 10
- Abstimmanlage
- FlipFlop
- DL und DTL
- RTL und RCTL
- Radio - Geschichte
- Radio 2
- Lausprecherweiche
- Radio 3
- Transformator
- Modulation
- Detektorempfänger
- Arbeitspkt Transistor
- Radio 4
- Thyristor
- Literaturverzeichnis
- Start HL-Elektronik
- Startseite
FlipFlop: Das Auffangflipflop
Nicht alle Probleme sind mit einem Grundflipflop lösbar. Zur Erinnerung nochmal die Schaltung des Grundflipflops mit NAND-Gattern:
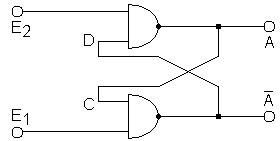
Will man z.B. zwei mehrstellige Dualzahlen stellenweise addieren, so muss sicher gestellt werden, dass die zueinander gehörenden Stellen nicht durcheinander geraten. Dies geschieht durch einen rechteckigen Taktimpuls:

... kein Problem mit einem astabilen Multivibrator.
Wir müssen eine Schaltung eintwickeln, bei der eine am Eingang bereitliegende Information erst dann eingeschrieben wird, wenn das Taktsignal ankommt. Wir schalten zwei NAND-Gatter vor, deren Ausgänge die Eingänge des Grundflipflops sind.
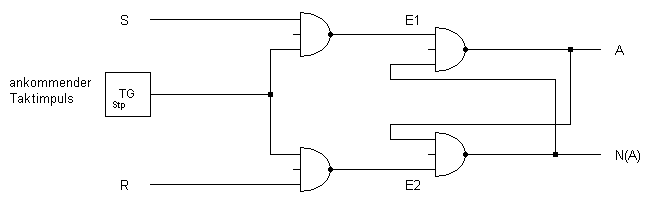
Diese Schaltung wird Auffangflipflop genannt. Ihr Schaltsymbol ist:
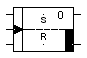
Aber funktioniert sie auch wie gewünscht? Denken wir das alles mal in Ruhe durch und zeigen zunächst, dass die Ausgänge A und N(A) im Grundzustand bleiben (dass also nichts passiert), solange der Taktimpuls Null ist.
-
Fall 1: T = O
- Die Eingänge E1 und E2 des Grundflipflops liegen auf L:
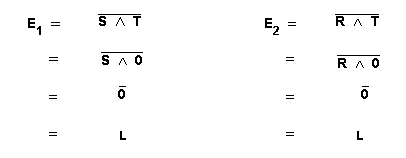
Da für den bistabilen Multivibrator (Grundflipflop) die folgenden Funktionstabellen gelten
| E1 | E2 | A1 | A2 |
| 0 | L | L | 0 |
| L | L | L | 0 |
und
| E1 | E2 | A1 | A2 |
| L | 0 | 0 | L |
| L | L | 0 | L |
kann man daraus folgern, dass die Ausgänge A und N(A) verschiedene Werte haben (je nachdem, welcher Transistor im bistabilen Multivibrator zuerst durchschaltet). Anders gesagt: Die Zustände von S und R spielen keine Rolle, solange der Taktimpuls Null ist, die Ausgänge bleiben unverändert..
Es gilt also:
| T | S | R | Ausgänge |
| 0 | 0 | 0 | bleiben |
| 0 | 0 | L | im |
| 0 | 0 | L | Grundzustand |
| 0 | L | L | . |
Als nächstes wollen wir zeigen, dass bei T=L A denselben Wert wie S hat und N(A) denselben Wert wie R hat (natürlich unter der Voraussetzung, dass S von R verschieden ist).
-
Fall 2: T = L
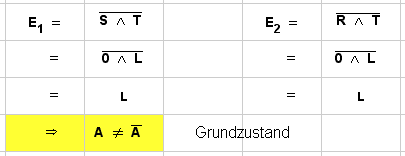
- . Zeile: S=R=0
- . Zeile: S=0, R=L
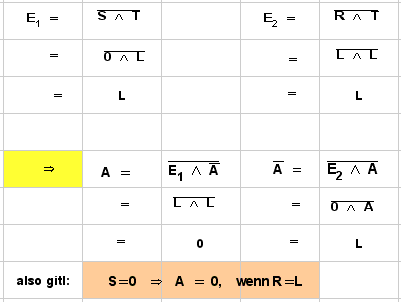
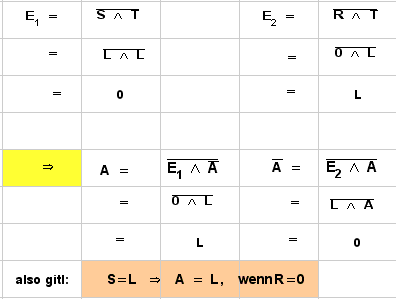
- . Zeile: S=L, R=0
- . Zeile: S=L, R=L
Wir untersuchen nun der Reihe nach die 4 möglichen Zustände von S und R, nämlich
| S | R |
| 0 | 0 |
| 0 | L |
| L | 0 |
| L | L |
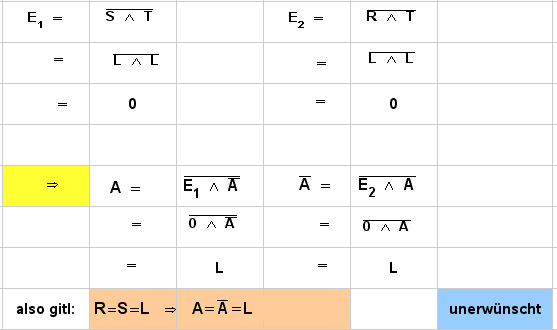
Es gilt also:
| T | S | R | Ausgänge |
| L | 0 | 0 | Grundzustand |
| L | 0 | L | A=0, N(A))L |
| L | L | 0 | A=L, N(A)=0 |
| L | L | L | A=N(A)=L |
-
Insgesamt gilt also für das Auffangflipflop:
Erst auf das Taktsignal T=L hin, kann eine Infomation gespeichert werden.
S heißt Setzeingang: Mit S=L wird A auf L gesetzt (bei R=0).
R heißt Rückstelleingang: Mit R=L wird A auf 0 gesetzt (bei S=0).
Beide Ausgänge haben nur unterschiedliche Werte, wenn mindestens ein Eingang auf 0 liegt.
| © 2010 Asti | PoVRay-Site | Mathematische Streiflichter |