Die Versiera (Witch of Agnesi) der Maria Gaetana Agnesi 2
Wenn man denn dem Internet (manchmal) glauben darf, dann
lebte Maria
Gaetana Agnesi von 1718 bis 1799.
Sie gehörte (als zweite Frau) der Universität von Bologna an, war Linguistin,
Philosophin und Mathematikerin. Mit "Instituzioni analitiche" leistete sie ihren
größten Beitrag zur Mathematik.
Die Versiera (lat.: versus, vertere - drehen, bewegen, mögl. verwechselt
mit altit.:l'avversiera - Hexe ... und so zu witch of Agnesi geworden, vielleicht hat
sich die Übersetzung ins Englische aber auch der Form des Hexenhutes angepasst) wurde von
ihr in Instituzioni analitiche beschrieben.
Ein Ursprungskreis mit Radius r wird um seinen Radius nach oben verschoben, im Abstand 2r wird eine
Parallele zur x-Achse gezeichnet. Ein Strahl vom Ursprung zu einem Kreispunkt P schneidet diese
Parallele im Punkt S. Der Bildpunkt P' liegt senkrecht unter S auf einer Parallelen zur x-Achse
in der Höhe des Kreispunktes P.
Bei Bewegung von P auf dem Kreis erhält man die Versiera. Eine gänzlich andere Kurve erhält
man, wenn man Q verschiebt, sodass M nicht mehr auf der y-Achse liegt.
|
|
Herleitung der Gleichung der Versiera in karteisischen Koordinaten
Betrachtet man die Strahlensatzfigur OSC,
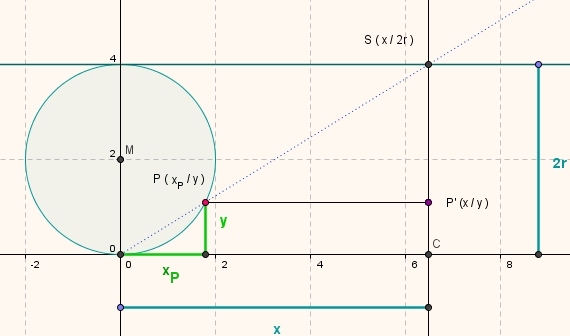
dann erkennt man, dass
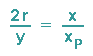
Diese Gleichung quadrieren wir und lösen sie dann nach xP2auf, da wir diesen Wert
anschließend in eine Kreisgleichung einsetzen müssen:
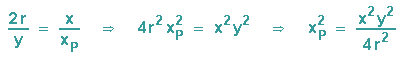
Der bewegliche Punkt P(xP / y) liegt auf einem Kreis, dessen Mittelpunkt auf der y-Achse um
r nach oben verschoben ist. Seine Koordinaten können also in diese Kreisgleichung eingesetzt werden:
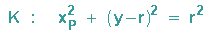
In diese Gleichung setzen wir nun unser "Strahlensatzergebnis" für xP2 ein und
erhalten nach dem Ausmultiplizieren der 2. bin. Formel und der Multiplikation mit dem
Hauptnenner 4r2:
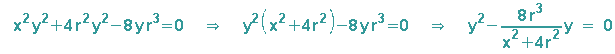
An dieser Stelle können wir uns entweder mit der quadratischen Ergänzung oder auch mit der p-q-Formel
vergnügen (Ausklammern von y ist natürlich auch möglich) und erhalten dann das Ergebnis:
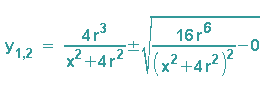
Dies führt uns zu zwei Lösungen:
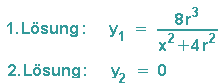
Die erste Lösung gilt für alle Punkte P, die sich auf der Kreislinie bewegen und vom Koordinatenursprung
verschieden sind, die zweite Lösung gilt für P(0/0) und liefert uns somit gleich die Asymptote.
... und im Netz aller Netze, wo so viele Leute heutzutage denken lassen, wird bei dieser Gleichung
(eine Herleitung habe ich nirgendwo gefunden) der Kreisradius nicht mehr r genannt, der Kreisdurchmesser
nicht mehr d genannt sondern a (vielleicht für 'a'bstand?)!
Herleitung der Parametergleichung der Versiera der Maria Agnesi
Betrachten wir nochmals das rechtwinklige Dreieck OCS aus obiger Abbildung (phi=Winkel(COS)):
Wir erhalten sofort:
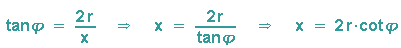
In diese erste Parametergleichung setzen wir aus der Darstellung mit kartesischen Koordinaten
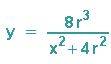
ein und erhalten die ff. Gleichung:
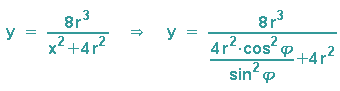
Wir denken uns im Nenner 4r2 ausgeklammert und können also den Bruch durch 4r2 kürzen, danach machen wir die Summanden im Nenner gleichnamig und erhalten:
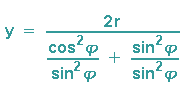
Im Nenner können wir nun einen Bruchstrich schreiben und durch Multiplikation mit dem Kehrbruch den Doppelbruch beseitigen.
Unser neuer Nenner wird zu 1, denn:
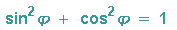
und schon haben wir unser Ergebnis:
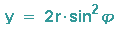
Für die Parameterdarstellung gilt also insgesamt:
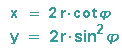
mit
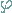= Winkel COS und r=Kreisradius.
... und weil mein Ergebnis mal wieder von WIKIPEDIA
abweicht, hier meine Quelle.
Aber ich trete auch den Beweis an, dass meine Quelle das richtige Ergebnis produziert hat:
Zum Abschluss noch die Inversion der Versiera am Einheitskreis: Man sieht, dass P' zum Ursprung strebt, wenn P gegen unendlich strebt:
Bemerkung: Es muss nicht der Einheitskreis um den Ursprung sein, mit gedrückter Maustaste ist auch der Inversionskreis verschiebbar.
Die Bahnkurve der Versiera musste hier mit kartesischen Koordinaten eingegeben werden, da sich der Punkt P bei der Parameterdarstellung nicht auf der Kurve festbinden lässt. (Ein Geheimnis von GEOGEBRA?)
| © 2024 Asti | PoVRay-Site |