Die Pascalsche Schnecke

  1. Definition
  2. Herleitung der Gleichung in kartesischen Koordinaten
  3. Herleitung der Gleichung in Polarkoordinaten
  4. Herleitung der Gleichung in Parameterdarstellung

... ist ein Sonderfall der gewöhnlichen Konchoide:

Der Punkt P bewegt sich auf einem Kreis, der durch den Ursprung verläuft und dessen Mittelpunkt auf der x-Achse liegt, der Bildpunkt P' bzw. P2 liegt auf der Verbindungsgeraden vom Ursprung zu P und hat von P den Abstand b.
Sowohl P' als auch P2 bewegen sich auf der "Schnecke".



r sei der Kreisradius, b sei der Abstand der Bildpunkte vom Kreispunkt P. .

Herleitung der Gleichung in kartesischen Koordinaten

Sucht man im Netz aller Netze danach, ist man schnell frustriert: Kaum jemand macht sich die Mühe zu erwähnen, dass der Kreismittelpunkt des Kreises, auf dem sich P bewegt, auf der x-Achse liegen muss, dass die Kreislinie durch den Ursprung gehen soll.
Aus der Abwesenheit der Koordinaten des Kreismittelpunktes in der Gleichung der P-Schnecke darf man das dann selber schlussfolgern. Manch einer nennt den Kreisradius a, manch einer nennt den Kreisdurchmesser a, die meisten erwähnen jedoch nicht, wofür sie sich entschieden haben (wo sie abgeschrieben haben.)

Na ja, ziehen wir mal wieder diese Quelle zu Rate und packen wir's an:



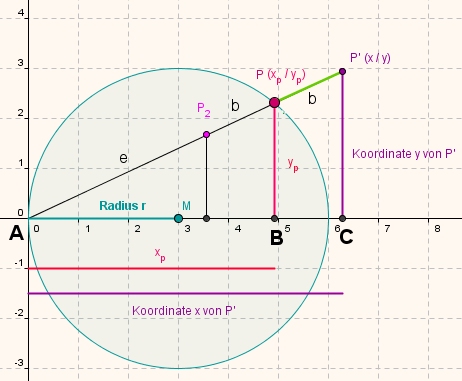
Sammeln wir zunächst mal alle Zusammenhänge, die wir aus obiger Abbildung gewinnen können:

a: P(xp/yp) liegt auf dem Kreis:




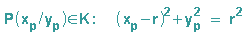
b: Auf die Dreiecke ABP und ACP' kann der Satz des Pythagoras angewendet werden:





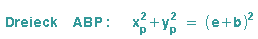
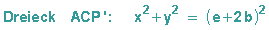
c: Die genannten Dreiecke bilden eine Strahlensatzfigur:



Unser Ziel ist eine Gleichung, die die Variablen x und y enthält, außerdem die bekannten Größen
r und b.
xP, yP und e sind unerwünscht, da unbekannt.

Beginnen wir damit, xP und yP rauszuwerfen: Wir lösen die Kreisgleichung (a) nach yP auf und erhalten:



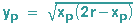
Dies wird in (b1), (b2) und (c) eingesetzt und liefert:



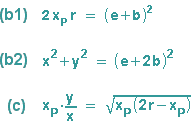
(b1) wird nach xP aufgelöst, das Ergebnis in (b2) und (c) eingesetzt:





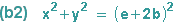
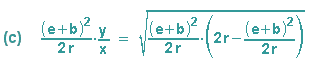
Der Radikand in (c) wird nun ausmultipliziert, anschließend werden seine Brüche gleichnamig gemacht. Der Hauptnenner im Radikand ist dann 4r2, wir können nun teilweise die Wurzel ziehen und erhalten:



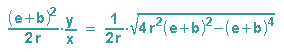
Wir klammern außerdem (e+b)2 aus und ziehen nochmals teilweise die Wurzel:



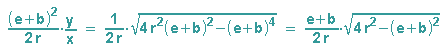
Die komplette Gleichung wird mit 2r multiplziert und durch (e+b) - das ja ungleich Null ist - gekürzt:



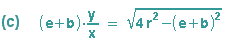
Wir können nun (b2) oder (c) benutzen, um nach e aufzulösen, das Ergebnis dann in die andere Gleichung einsetzen und erhalten so unser Endergebnis. Beide Varaianten führen zu etwas unangenehmen Termumformungen.

Wir nehmen die Gleichung (c), quadrieren sie und klammern anschließen (e+b)2 aus:



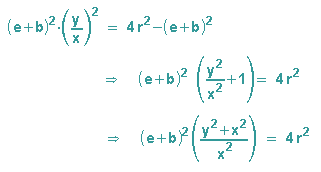
und



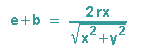
Um dies in (b2) einzusetzen, müssen wir noch b addieren, dann können wir e+2b in (b2)einsetzen:



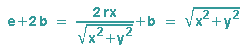
... und sind fast fertig. Zunächst wird die Gleichung mit der Wurzel multipliziert, die Wurzel wird dann isoliert, dann wird die Gleichung quadriert und wir haben unser Endergebnis:



liefert



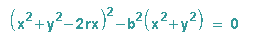
... dabei ist r der Kreisradius, b der Abstand der Bildpunkte P' und P2 vom Kreispunkt P.



Herletung der Gleichung in Polarkoordinaten

Für die Herleitung "von Anfang an" brauchen wir die Darstellung des Kreises mit M(r/0) in Polarkoordinaten:

(a)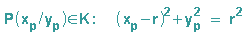

Außerdem gilt

(b)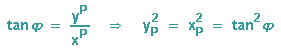

Wir setzen (b) in (a) und formen um:



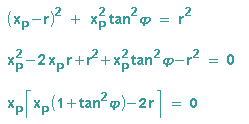
Die Faktoren die Produktes werden einzeln Null gesetzt und es ergeben sich die beiden Lösungen:



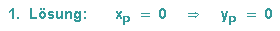
und



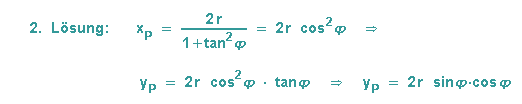
Bemerkung: Bei der 2. Lösung wurde der Zusammenhang zwischen Tangens und Kosinus benutzt:






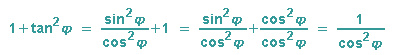
Für die Polardarstellung der Pascalschen Schnecke wird nun der Satz des Pythagoras auf das
Dreieck ABP angewendet, für xP und yP werden dann die obigen Lösungen eingesetzt:



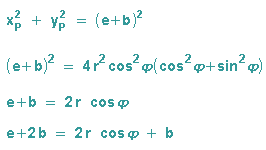
Daraus erhalten wir das Endergebnis für den äußeren Punkt P' und den inneren Punkt P2:






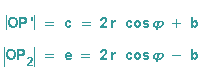
Herleitung der Parameterdarstellung der Pascalschen Schnecke

Für die Parameterdarstellung müssen die Koordinaten x und y der Punkte P' und P2 in Anhängigkeit des Drehwinkels dargestellt werden.
Betrachten wir das Dreieck ACP' in der 2. Abbildung auf dieser Seite und bilden den Kosinus des Drehwinkels:



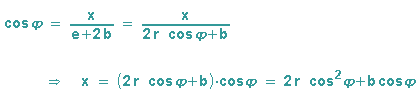
Dabei wurde für e+2b das Ergebnis aus der Polardarstellung eingesetzt.

Als nächstes wird der Sinus des Drehwinkel im Dreieck ACP' gebildet, wieder wird e+2b ersetzt:



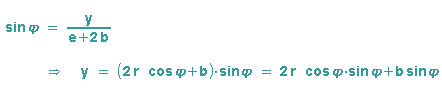
Für den "inneren Punkt" P2 wird das kleine Dreieck betrachtet, wieder wird der Kosinus und der Sinus des Drehwinkels gebildet, e wird durch das Ergebnis aus der Polardarstellung ersetzt:




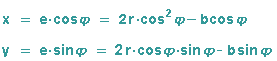
© 2010-2024 Asti PoVRay-Site