Die Konchoide des Nikomedes
Die eigentliche Konchoide - Punkt P bewegt sich auf einer Geraden - wurde schon von Nikomedes im antiken Griechenland
beschrieben.
Zur Herleitung der Gleichung soll die Gerade parallel zur x-Achse verlaufen:
Mit dem Schieberegler a wird der Abstand der Gerade von der x-Achse, mit dem Schieberegler b wird der Abstand des
Bildpunktes von P festgelegt:
Man kann nun die drei Fälle a<b, a=b und a>b untersuchen.
Für a<b hat die untere "Muschelschale" eine Schlaufe, für a=b hat sie eine Spitze, für a>b ist weder Schlaufe noch Spitze vorhanden.
Die Herleitung der Gleichung in kartesischen Koordinaten:
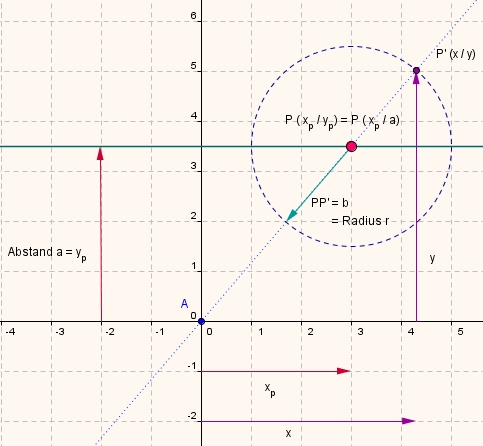
Der Bildpunkt P' bewegt sich auf einem Kreis um den Punkt P mit der Gleichung
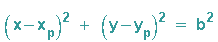
Aufgrund der Strahlensätze gilt:
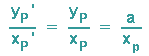
Durch Umformung dieser Gleichung erhält man:

Dies wird nun in die Kreisgleichung eingesetzt:
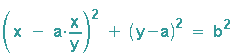
In der linken Klammer macht man gleichnamig (Nenner y) und mutlipliziert dann die Kreisgleichung mit y2, das Ergebnis ist:
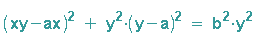
In der linken Klammer wird nun x ausgeklammert
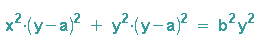
... und eine nochmalige Anwendung des Distributivgesetztes ergibt:
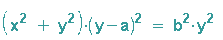
Wir haben's geschafft!
Die Herleitung der Gleichung in Polarkoordinaten aus der kartesischen Darstellung:
r sei der Abstand des Bildpunktes P' vom Koordinatenursprung, also r = lOPl + b.
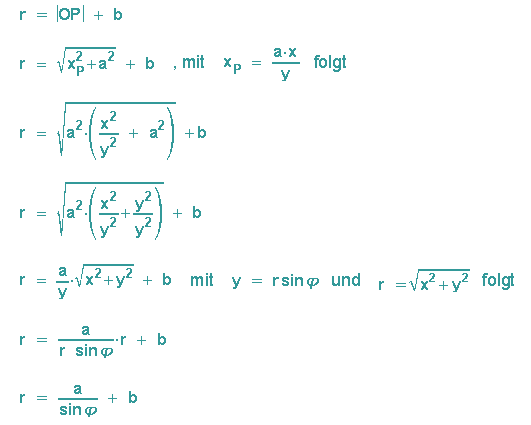
Für den ursprungsnäheren Bildpunkt P1 wird +b durch -b ersetzt.
Die Herleitung der Gleichung in Parameterdarstellung
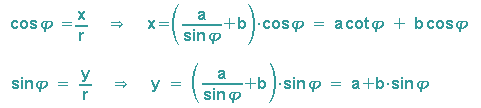
...gefolgt von einem nicht ganz unwahrscheinlichen Dialog aus der Unterrichtspraxis:
Schüler/in: Bei WIKIPEDIA steht aber
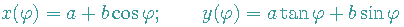
Lehrer/in: Sehen Sie einen Fehler in unserer Herleitung?
Schüler/in: Eigentlich nicht, aber WIKIPEDIA lügt doch nicht.
Lehrer/in: Wie hat WIKIPEDIA denn die Parameterdarstellung hergeleitet?
Schüler/in: Dazu habe ich nichts gefunden?
Lehrer/in: Hat WIKIPEDIA denn auch so eine Abbildung wie unsere?
Schüler/in: Na ja, Punkt P wird dort zwar B genannt, aber bewegt sich auch auf einer Geraden, der Abstand zum Bildpunkt heißt dort auch b, und a wird auch genauso verwendet.
Lehrer/in: ... und wo kommt nun der Unterschied in den Formeln von uns und WIKIPEDIA her?
ES KLINGELT!
... und hier liegt der Hund begraben!
| © 2010 Asti | Links für Unterricht | PoVRay-Site |