Die platonischen Körper und Alan St. George

Alan St. George, Brite, Architekt im Ruhestand, lebt in Portugal und verfertigt mathematische Skulpturen, u. a. fraktale Variationen über die regulären (platonischen) Körper.



Euklid bewies, dass es genau 5 Körper gibt, die derart von regelmäßigen Vielecken begrenzt werden, dass sich in jeder Ecke die gleiche Anzahl von Seitenflächen in gleicher Weise treffen.

Tetraeder, Würfel, Oktaeder, Dodekaeder und Ikosaeder(4-flach, 6-flach, 8-flach, 12-flach und 20-flach)


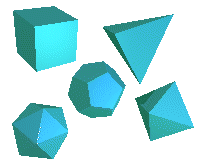Alan St. George klebt auf diese Körper in bestimmter Anordnung kleinere Körper derselben Art, sodass ein anderer platonischer Körper entsteht. Als Beispiel sei vorgestellt, wie aus einem Würfel ein Oktaeder entsteht:



Wer kennt ihn nicht, Rubic´s Cube? Nach Art dieses Spielzeugs wird zunächst der Ausgangswürfel in 27 kleinere Würfel zerlegt. Nimmt man nun sechs kleine Würfel, deren Kantenlänge der eines der Teilwürfel entspricht und bastelt daraus ein Kreuz, auf das nochmals ein kleiner Würfel gesetzt wird, so kann man dieses Gebilde auf je eine der 6 Seitenflächen von "Rubic´s Cube" setzen, und erhält dann schon näherungsweise ein Oktaeder. . In der Abbildung sind die aufgesetzten Würfel zur Verdeutlichung etwas verkleinert dargestellt. Der so entstehende Körper hat als Begrenzung lauter kleine Quadrate. Auf jede dieser Quadratflächen setzt man nun wieder das Kreuz mit dem aufgesetzten Würfel, wobei die neue Kantenlänge inzwischen 1/9 der ursprünglichen Kantenlänge beträgt. Bastelfreunde haben´s nun schwer: auf unseren Ausgangswürfel müssen sie 36 mittelgroße Würfel aufkleben, 6 mal 21 freie Quadratflächen entstehen, dazu 6 mal 4 freibleibende Quadrate auf unserem Ausgangswürfel: wer hat die Geduld, 150 kleine Würfel zu basteln? Auch wer schon bei den 36 halbgroßen Würfeln die Bastelarbeit stoppt, erkennt, dass man auf diese Weise einen Würfel zum Oktaeder fraktalisieren kann.



Alan St. George hat mit seinen Skulpturen den Übergang von Würfel, Tetraeder und Oktaeder zu jedem anderen dieser drei Körper realisiert. (Wer wissen will, wie´s geht, der lese doch mal in "Spektrum der Wissenschaft", 10/97, nach - wenn man die denn zuhause gesammelt hat. Link ins Internet zu dieser Ausgabe.)

• Zum Seitenanfang

In Euklid´s (griechischer Mathematiker, ca. 365 v.Chr. bis ca. 300 v. Chr.) Hauptwerk "Elemente", einer 13-bändigen Abhandlung über die Mathematik (ebene Geometrie, Abbildungen, Eigenschaften von Zahlen, ...), wird die sog. "euklidische Geometrie" formuliert, die bis ins 19. Jahrhundert die Grundlage der Geometrie überhaupt bildetete. 1482 erschien in Venedig die erste Übersetzung aus dem Arabischen ins Lateinische. Euklid, der vermutlich bei Schülern Platos lernte, unterrichtete in Alexandria Geometrie und gründete dort auch eine Schule für Mathematik. Ihm werden auch verschiedene Entdeckungen aus dem Bereich der Zahlentheorie zugeschrieben.

• Zum Seitenanfang