Anleitungen - R bis Z
- Regenbogen
- rgbt und rgbf
- Rotation und SOR
- Spiralen
- Trochoiden
- üb.gel.Texturen
- Vektorfunktionen
- Schleifen
- Splinetree
- Superellipsoid
- Texte
- Zufallszahlen
- Startseite - Theorie
- Startseite
rgbt und rgbf
Mit
color rgb <0.8,0,0.3>
wird der verwendete Farbwert durch seine rot/grün/blau-Anteile festgelegt. Mit
color rgbf <0.8,0,0.3,1>
und
color rgbt <0.8,0,0.3,1>
werden 2 möglich Arten von Transparenz in POVRAY, filter und transmittance bestimmt:
- Bei rgbf bedeutet der Wert 1, dass die gewählte Farbe vollständig transparent ist, das Licht jedoch in der Art einer gefärbten transparenten Folie filtert,
- bei rgbt wird das Licht der gewählten Farbe vollständig durchgelassen.
Surface of Revolution
Bei der Berechnung von Rotationskörpern sollten mindestens 4 Punkte verwendet werden, jeweils Radius und Höhe sind in dieser Reihenfolge anzugeben, die Höhenwerte müssen ansteigen. Die Krümmung sollte nicht zu scharf sein, da die Annäherung nicht durch lineare Funktionen erfolgt.
Ein Beispiel für die zugehörige Syntax:
#declare Vase =
sor { 8,
<0.0 ,-0.1 > //Beginn des Körpers mit Radius 0
<2.5 ,0.1 >
<2.5 ,1.5>
<1.8 ,1.65 >
<0.5 ,2.65 >
<0.6 ,6.65 >
<1.5 ,7.65 >
<4.8 ,9 >
open
}  |
 |
Trochoiden und Bewegungsfunktionen
Die Idee stammt aus dem Bewegungsmodul der sehr sehenswerten Matheprisma-Seite der Uni Wuppertal.
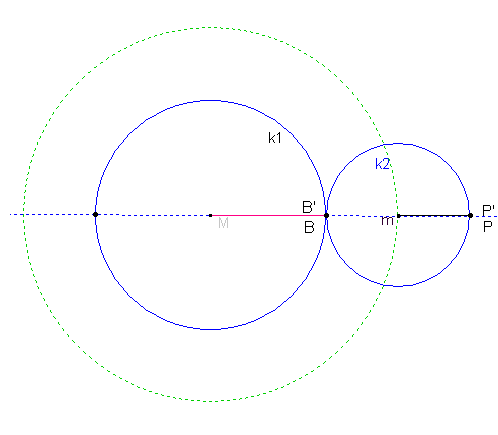
Zeichnet man zwei Kreise, die einander berühren und lässt die Kreislinie des einen auf der anderen abrollen, so muss man sich nur noch einen Punkt auf oder in der Nähe der kleinen Kreislinie denken, der mit rotiert, und schon ergibt dessen Ortslinie
eine TROCHOIDE. Der in der Abbildung äußere Kreis kann auch im Innern des Ausgangskreises abrollen.
Bemerkung zur Namensgebung:
Liegt der zu beobachtende Punkt auf der Kreislinie des abrollenden Kreises, so wird die Bahnkurve oft als Zykloide bezeichnet, die Bezeichnung Trochoide wird dann für Bahnkurven von Punkten benutzt, die innerhalb oder außerhalb des abrollenden Kreises liegen.
Rollt der kleine Kreis gegen den Uhrzeigersinn auf der Kreislinie des großen ab, dann bewegt sich P auf dem kleinen Kreis nach P'. Um dieselbe Kreisbogenlänge ist dann der Berührpunkt B der beiden Kreise auf dem großen Kreis gegen den Uhrzeigersinn gewandert. Der neue Berührpunkt sei dann B'.
Die Bogenlängen PP' und BB' sind gleichlang.
 |
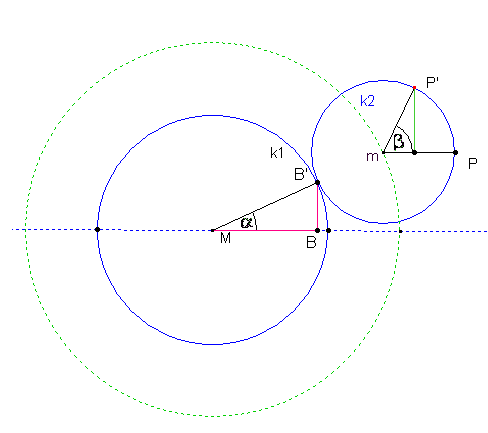 |
Um die Linie, auf der der Punkt P sich bewegt, genauer untersuchen zu können, suchen wir zunächst einen Zusammehang zwischen den Winkeln
 und ß und beachten dabei die gleiche Länge der genannten Kreisbögen.
und ß und beachten dabei die gleiche Länge der genannten Kreisbögen.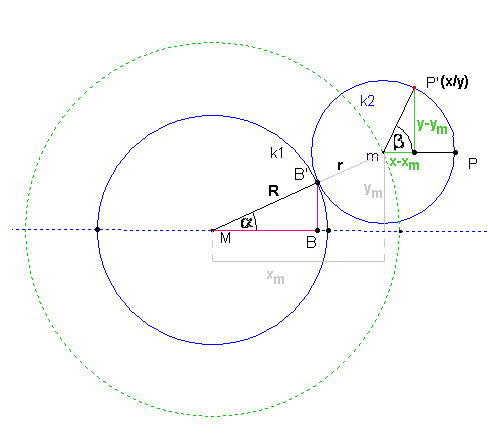 |
Anhand der letzten Abbildung erkennt man nun die folgenden Zusammenhänge:
Für die beiden Kreisumfänge gilt:
 |
Für die Kreisbögen gilt dann:
 |
Da beide Kreisbögen gleichlang sind, folgt daraus:
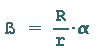 |
Anhang der 3. Abbildung erkennt man, dass:
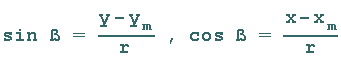 |
Woraus die Gleichungen für die Koordinaten von P(x/y) folgen:
 |
Programmiert man nun eine solche Ortslinie, dann können die Werte für R und r frei gewählt werden (negative Werte für r bewirken, dass der kleine Kreis innerhalb des großen Kreises abrollt).
Ein programmiertes Beispiel:
 < < |
#macro Mache_rahmen (Aussenradius)
union{
#local R_gross=Aussenradius;
#local R_klein=R_gross/15;
#local faktor=1/255;
#declare Alpha=.1;
#while (Alpha<360.05)
#declare Beta= R_gross/R_klein*Alpha;
#declare xm=(R_gross+R_klein)*cos(Alpha);
#declare ym=(R_gross+R_klein)*sin(Alpha);
//Der Punkt P muss nicht auf der kl. Kreislinie liegen!
//verändert xm und ym!
#declare X=R_klein*cos(Beta)+xm;
#declare Y=R_klein*sin(Beta)+ym;
sphere{<X,Y,0>,.075//Der Kugelradius bestimmt die Rahmendicke
pigment {color rgb<148,199,222>*faktor}
finish{F_MetalA}
}//ende kugel
#declare Alpha=Alpha+0.25;
#end //end while
}//end union
#end //Ende des Makros
Mache_rahmen(3.1) //Makro aufrufen
Eine Trochoidenanimation:
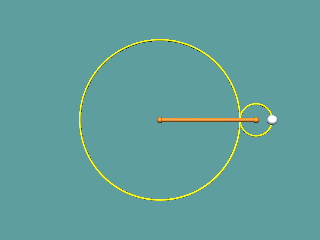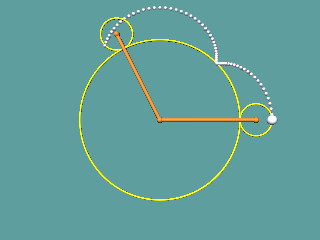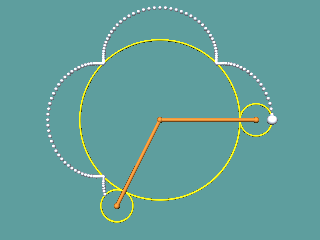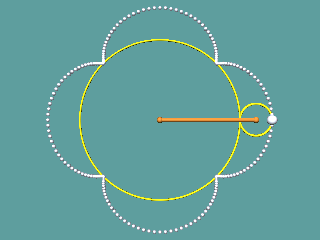 |
Weitere Animatione und Arten von Trochoiden, Zykloiden, ... findet Ihr auf meiner Seite Mathematische Streiflichter.
Auch als Programmierung von Bilderrahmen sind Trochoiden gut geeignet:
 |
Übereinandergelegte Texturen (layered textures)
Mehrere teilweise transparente Texturen werden übereinandergelegt, um eine komplexe Textur zu erzeugen. Dabei werden einfach 2 oder mehr Texturen nacheinander aufgelistet Die Umwandlungszeit wird hierbei allerdings verlängert.
sphere {
texture { T1 } // die unterste Textur
texture { T2 } // eine halbtransparente mittl. Textur
texture { T3 } // eine halbtransparente obere Textur
} //Ende der Kugel
Dabei müssen die Schlüsselwörter pigment und finish innerhalb der geschweiften Textur-Klammern stehen!
Beispiele
Im folgenden Bild sieht man durch die Texturen pigment {Peel} und gefärbtes Glas noch die innere Kugel mit der Textur pigment{Blood_Sky} hindurchschimmern:
 |
 |
Vektorfuntkonen
Zu PovRay gehören u.a. eingebaute Vektorfunktionen. Ihnen können ein oder mehrere Argumente übergeben werden, der Funktionswert (Rückgabewert) kann ein Vektor oder eine Zahl sein. Drei dieser Funktionen sollen hier näher betrachtet werden.
I. VAXIS_ROTATE(A,B,F)
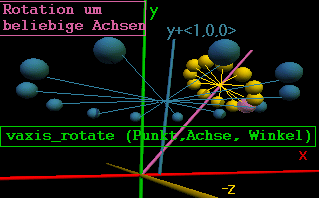 |
Als erste Vektorfunktion stelle ich vaxis_rotate(A,B,F) vor.
A ist dabei ein gegebener Punkt P(x,y,z), B ist der Vektor, durch den die gewünschte Drehachse dargestellt wird, F ist der Drehwinkel.
In der Abbildung wurde vaxis_rotate zweimal verwendet:
- der cyanfarbene Kugelkranz
- der blaue Kugelkranz
#declare Winkel=0;
#declare Drehvektor=<4,5,0>;
#declare zaehler=0;
#while (Winkel<361)
#local Mittelpunkt=vaxis_rotate(<7,5,0>,Drehvektor,Winkel);
sphere { Mittelpunkt , 0.5
pigment {color Yellow }
no_shadow
}
#local Winkel=Winkel+30;
#end
<7,5,0> ist dabei der Mittelpunkt der lilafarbenen Ausgangskugel, der Drehvektor ist in der gleichen Farbe gezeichnet, um die Drehebene zu verdeutlichen, wurden mit einem Pixelgrafikprogramm zusätzlich "Speichen" eingezeichnet. Sämtliche Vektoren werden vom Koordinatenursprung aus benannt, will man daher eine Rotation um einen Drehvektor, der nicht durch <0,0,0> geht, so muß man mit Parallelverschiebungen arbeiten. Dies wird durch den Skriptteil, der zum blauen Kugelkranz gehört, verdeutlicht:
#declare Winkel=0;
#declare Drehvektor=y;
#declare zaehler=0;
#while (Winkel<361)
#local Mittelpunkt=vaxis_rotate(<7,5,0>,Drehvektor,Winkel);
#local Mittelpunkt=Mittelpunkt+<1,0,0> //Verschiebung 1 LE nach rechts;
sphere { Mittelpunkt,.5
pigment {color cyan}
no_shadow
}
#declare Winkel=Winkel+30;
#end
Die Parallelverschiebung in der 2. Mittelpunkts-Definition muss auf jeden Punkt angewandt werden, was dann bei Körpern wie box oder cylinder zu etwas mehr Tipparbeit führt.
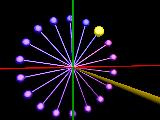
VROTATE(A,B)
Für eine Drehung um den Koordinatenursprung kann vrotate(A,B) benutzt werden: A ist dabei der Vektor vom Koordinatenursprung zu einem gegebenen Punkt P(x,y,z). B ist der Drehvektor, durch dessen Komponenten festgelegt wird, um welche Koordinatenachse und um welchen Winkel der gewünschte Punkt gedreht wird. Besser als Worte sind die ff. drei Abbildungen:

|

|
|
| B = <10,0,0> | B = <0,10,0> | B = <0,0,10> |
Ausgangspunkt A ist jeweils der Mittelpunkt der gelben Kugel. Der Drehvektor wird in einer Zählschleife um B vergrößert (vgl. die zugehörigen Skripte, die durch Mausklick auf die Abbildungen einsehbar sind).
Schönere Bewegungsabläufe für evtl. Animationen erhält man durch Kombinationen der Rotation um 2 oder 3 Achsen:

|

|

|
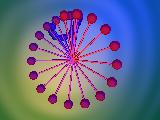
|
- Bild 1: x- und y-Achse
- Bild 2: x- und z-Achse
- Bild 3: y- und z-Achse
- Bild 4: x-, y- und z-Achse
Beispiele: Die beiden ersten Bilder sind mit VROTATE programmiert, das letzte mit VAXIS_ROTATE.
 |
 |
 |
VLENGTH(A)
Diese Vektorfunktion misst den Abstand des Punktes A vom Koordinatenursprung und ist identisch mit vlength (A - <0,0,0>). Der Rückgabewert ist also eine Zahl, kein Vektor.
Im ersten Bild wurde vlength benutzt, um abhängig vom Abstand zum Nullpunkt die Farbe der Kugeln festzulegen. Im zweiten Bild wird vlength eingesetzt, um den Blauanteil in der Farbe der Spiralenscheiben in Abhängigkeit vom Abstand zum Nullpunkt zu erhöhen.
 |
 |
Im Folgenden einige einige mit Vektorfunktionen erzielte Bildeffekte:
 |
 |
 |
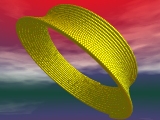 |
 |
 |
 |
 |
 |
 |
 |
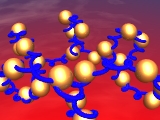 |
 |
 |
 |
 |
 |
 |
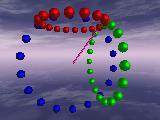 |
 |
 |
 |
 |
 |
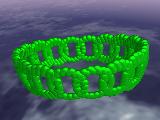 |
 |
 |
Zählschleifen
Beim Programmieren ist es oft nötig, daß ein Programmteil mehrmals durchlaufen wird. Dies kann durch Einbau einer Zählvariablen geschehen oder durch eine Wiederholung mit Anfangs- oder Endbedingung.
WHILE (i>0) ..... END
Solange der Zähler i > 0 ist, wird der Teil des POVRAY-Skriptes durchlaufen, der zwischen WHILE und END steht.
Beispiel:
#declare i=30;
#while (i>0)
#local X=i*10;
cylinder{<300-X,0,0>,<300,300-X+10,0>,2
pigment {color Silver}
finish{F_MetalA}
translate <-150,-150,0>
no_shadow}
#local i=i-4;
#end
Zunächst wird der Wert des Zählers i=30 gesetzt. Die nun folgende while-Schleife zeichnet Zylinder (die "Schnüre" in der Abbildung unten), die bei der zählerabhängigen Position X starten, dabei ist X immer das 10-fache des Zählers i.
Wichtig ist die Änderung für i in der vorletzten Zeile der Schleife: i wird jeweils um die Zahl 4 verkleinert. Falls diese Zeile fehlt, entsteht eine Endlosschleife, da i immer größer als 0 bleibt, das Programm stürzt ab.
 |
 |
 |
 |
 |
| Andrew's POV Place | |
 |
Auf Andrews sehr sehenswerter Seite findet ihr zwei INCLUDE-Dateien, mit deren Hilfe realistisch aussehende Bäume erzeugt werden können. Auch einige Beispielskripte für Pov-Bäume sind zur Verfügung gestellt. Skripte und INCLUDE-Dateien sind sehr gut dokumentiert. ... ein Klick aufs Bild führt zu seiner Seite. |
| An dieser Stelle ein Dankeschön an Andrew! | |
Die Bilder auf dieser Seite sind mit SPLINETREE.INC und LEAFSDEF.INC von Andrew erstellt.
Zunächst ein Beispiel mit Ahornblättern (die zugehörigen TGA-Bildvorlagen werden ebenfalls von Andrew zur Verfügung gestellt). Durch die gute Skriptdokumentation ist es einfach, Änderungen anzubringen und die Bäume nach eigener Vorstellung zu gestalten. Die Grafik für die Blätter wurden auf Kugeln projiziert, was zur Folge hat, dass bei Verwendung von Nebel die Kugeln noch leicht sichtbar sind. Ein Mausklick aufs Bild zeigt (wie überall auf meiner Seite) das Pov-Skript, das aus einer von Andrews Beispieldateien entstanden ist.
 |
Das Bäumchen im 2. Bild ist mit "eigenen" Blättern ausgerüstet.
Man benötigt ein Zeichenprogramm, das mit Ebenen und Masken arbeiten kann.
- Zunächst mal ein geeignetes Bild einscannen oder auch - wenn vorhanden - mit der Digitalkamera fotografieren und einlesen.
- Den "Zauberstab" so einstellen, dass mit ihm genau die Blattform ausgeschnitten werden kann.
- Das Blatt ohne Hintergrund kopieren und in ein neues Bild mit transparentem Hintergrund einfügen.
- Eine neue Ebene erstellen, dazu eine Maske aus der Auswahl mit invertierten Farben in den Alphakanal speichern. Das sieht dann so aus: (links das Skindapsusblatt, rechts der Alphakanal)

- Das Bild kann nun für die Bildprojektion auf eine Kugel benutzt werden (vgl. Skript).
 |
 |
 |
 |
Superellipsoid
Das superquadric ellipsoid ist eine Erweiterung des quadric ellisoid (zur Erinnerung: quadrics sind Polynome 2. Grades). Es dient zur Erzeugung von Quadern, Zylindern u. a. Körpern mit gerundeteten Ecken und wird durch die ff. Funktion dargestellt:
f(x, y, z) = ( |x| 2/e + |y| 2/e) e/n + |z| 2/n - 1 = 0
e bwz. n werden Ost-West- und Nord-Süd-Koeffizient genannt und bestimmen die Ellipsoidgestalt.
Die Syntax ist
superellipsoid { < e, n > }
Box mit abgerundeten Ecken:
#declare Rounded_Box = superellipsoid {< r, r >
Zylinder mit abgerundeten Ecken:
#declare Rounded_Cylinder = superellipsoid {< 1, r > }
Die Stärke der Rundung wird durch
0 < r < 1
bestimmt: je kleiner r, desto kantiger die Ecken.
Die beiden Koeffizienten e und n sollten zwischen 0 und 1 liegen, jedoch ergeben sich auch für negative Werte und Werte größer als 1 teilweise interessante Objekte. Startet man bei e=1 und n=1 (Kugel) und variiert man dann systematisch einen oder beide Koeffizienten, so kann man sich einen guten Überblick über die Möglichkeiten verschaffen.
 |
 |
 |
 |
Textobjekte
Das Textobjekt gehört zu den einfachen Objekten, die für CSG (Constructive Solid Geometry) benutzt werden können. Es kann verschoben, skaliert und rotiert werden. Eigenschaften wie Textur, Farbe, ... können wie üblich zugeordnet werden.
text {
ttf "c:\windows\fonts\tahomabd.ttf" "PovRay" 1.9, <0.3,0.1,16>
scale <...>
rotate <...>
translate <...>
texture{...}
finish {...}
}
- Der Verzeichnispfad für die Schriftart muss selbstverständlich dem eigenen PC angepasst werden.
- Die Zahl nach der in Gänsefüßchen eingeschlossenen Zeichenkette steht für die "Tiefe" der Buchstaben,
- der nachfolgende Vektor steht für den OFFSET, d.h. die Verschiebung der einzelnen Buchstaben in x-Achsen-, y-Achsen- und in z-Achsenrichtung.
 |
 |
Verwendung von Zufallszahlen mit PoVRay
Pascalprogrammierer/innen kennen die Funktion RANDOM, die Zufallszahlen zwischen 0 und 1 (inklusive) erzeugt und mit dem Befehl randomize initialisiert werden muss, damit nicht immer dieselbe Folge von Zahlen entsteht. Analog dazu bietet POVRAY die Funktionen RAND, die aus einer Folge von Zufallszahlen von Null bis Eins eine ausgibt, und SEED, mit der ein Startwert festgelegt wird, um gleiche Zahlenfolgen zu vermeiden.
Verwendbar sind rand und seed, wenn z.B. eine Folge von Objekten zufällig verteilt werden oder aber eine Farbe zufällig variiert werden soll.
 |
Zunächst werden VERSCHIEBUNG (für die Position der Kugelmittelpunkte) und KUGELRADIUS definiert:
#declare VERSCHIEBUNG = seed(17); #declare KUGELRADIUS = seed(15);
Sinnvoll ist eine Abfrage, die bewirkt, dass nur diejenigen Kugeln gezeichnet werden, deren Abstand vom Koordinatenursprung eine bestimmte Entfernung nicht überschreitet, nur so ist man sicher, dass im geünschten Bildausschnitt auch die gewünschte Kugelzahl ist.
Dazu wird die Funktion vlength benutzt, die die Länge des Vektors vom Punkt <0,0,0> zum Kugelmittelpunkt <xm, ym, zm> berechnet:
vlength(Mittelpunkt)
Im Deklarationsteil werden drei neue Größen Abstand, Kugelzahl und Anzahl deklariert. Nur wenn die Länge des Mittelpunktvektors kleiner als Abstand ist, wird die Variable Kugelzahl um eins erhöht, sobald Kugelzahl so groß wie Anzahl ist, wird der Schleifenzähler j auf seinen höchsten Wert gesetzt, und die Schleife wird beendet.
Hier also die komplette Zählschleife:
#local j=0;
#while (j<500)
#local Mittelpunkt=<(rand(VERSCHIEBUNG)-.5)*10,
(rand(VERSCHIEBUNG)-.5)*10,
(rand(VERSCHIEBUNG)-.5)*10>*2;
#if (vlength(Mittelpunkt)<Abstand)
#sphere { Mittelpunkt, rand(KUGELRADIUS)*2
pigment{color rgb<rand(VERSCHIEBUNG),
rand(VERSCHIEBUNG)-.2,
rand(VERSCHIEBUNG) >}
finish{F_MetalA}} //end sphere
#local kugelzahl=kugelzahl+1;
#if (kugelzahl=Anzahl+1) #local j=499; #end
#else
#local j=j+1;
#end //end if
#local j=j+1;
#end //end while
 |
... und noch zwei Beispiele dazu:
 |
 |
| © 2010 Asti | PoVRay-Site | Mathematische Streiflichter | Algorithmische Kunst |
|