Liest man die Erläuterungen von Scott Draves,



dann tauchen schon gleich zu Anfang einige Fachbegriffe auf, die nicht Jedem vertraut sind: Fraktal, IFS, Chaosspiel, Attraktor, ....

Interaktiv und gut verständlich erklärt sind diese Begriffe in Ulrich Schwebinghaus' Modul "Fraktale und das Chaosspiel" auf der Matheprismaseite der Uni Wuppertal. In Anlehnung an dieses Modul will ich hier versuchen, in gekürzter Form und dennoch verständlich, diese Begriffe zu erläutern.

Grundlegende Begriffe, wie FRAKTAL, FUNKTION, ITERATION, LOGARITHMUS, ... findet ihr bei den Schaltflächen oben an der Seite. Bei Anwahl einer der Schaltflächen wird jeweils eine neue Seite geöffnet.

1. FRAKTAL
   
   Zu diesem Begriff habe ich auf meiner Matheseite einen Einstieg ins Thema erstellt (siehe Schaltfläche 'FRAKTAL' oben an der Seite). Hier nur kurz:
   Fraktale Formen oder Muster haben eine hohe Selbstähnlichkeit (Teile der Form sind Kopien der Gesamtform, wie z. B. das Farnblatt), evtl. eine exakte Selbstähnlichkeit (jeder beliebige Teil der Form enthält eine Kopie der Gesamtform), ihre Dimension ist nicht ganzzahlig sondern gebrochen.



2. Kontrahierende Abbildung
   
   Nimmt man 2 Startpunkte P und Q und wendet auf sie eine geometrische Abbildung f an (z.B. zentrische Streckung, Drehstreckung,...) und ist dann der Abstand der Bildpunkte f(P) zu f(Q) kleiner als der Abstand der Startpunkte P zu Q, dann wird die Abbildung f kontrahierend oder zusammenziehend genannt. Für die zentrische Streckung und Drehstreckung (Genaueres zu diesen Abbildungen findet Ihr auf meiner Mathematik-Seite) gilt dies, wenn der Streckfaktor kleiner als 1 ist.



3. Das CHAOSSPIEL
   
   Wählt man einen beliebigen Startpunkt, nimmt man sich eine Menge geometrischer Abbildungen, wählt aus dieser Menge jeweils eine Abbildung zufällig aus und führt damit eine Iteration aus, dann erhält man das sog. Chaosspiel.



4. IFS
   
   Die Abbildungen f₁, f₂, ...., f_n, die für die Zufallsauswahl bei jeder Iteration zur Verfügung stehen, nennt man Iteriertes Funktionensystem (auch iteratives Funktionensystem, auch IFS)



5. Attraktor
   
   Mit einem Würfelspiel nach einer Idee von Jürgen Giesens Vortrag "Chaosforschung - Fraktale - Chaos - Ordnung" , zu dem man im Internet hier auch ein Applet findet, kann man ein solches Chaosspiel mal ausprobieren. Nach hinreichend vielen Würfen entsteht dann allmählich das allseits bekannte Sierpinski-Dreieck. Schon bei ca 1000 Würfen ist es einigermaßen erkennbar.
   
   Eine solche Figur wird dann Attraktor genannt. Jedes kontrahierende IFS hat einen eindeutigen Attraktor.



6. Beispiele aus dem Artikel von Scott Draves
   
   In Apophysis wird nun das System von affinen Abbildungen (diese sind umkehrbar und Geraden werden wieder auf Geraden abgebildet, Genaueres für mathematisch Interessierte ist über die Schaltfläche oben nachlesbar) erweitert:
   
   Es werden auch nicht-lineare Abbildungen mit affinen kombiniert (sog. 'variations'). Beispiele sind lt. Scott Draves:
   
   
   
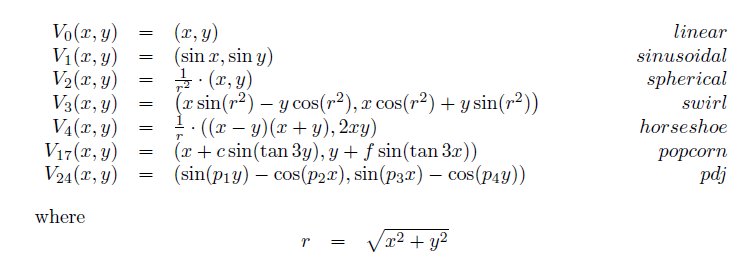
   Weitere affine Abbildungen werden dann in Apophysis 'post transforms' genannt. Dazu kann pro 'flame' dann noch eine sog. 'final transform' kommen.
   



7. Färben der Punkte
   
   
   Untersucht man, welche Teile des Attraktors von welcher Abbildung erzeugt wurden, so kann man das zur Einfärbung der Punkte benutzen. Für zu dunkle Punkte wird dann noch eine Gamma-Korrektur eingefügt. Genaueres kann in Scott Draves Kapitel 'Coloring' nachgelesen werden.

... und wer tiefer in die hinter Apophysis stehende Mathematik einsteigen will, muss sich an dieser Stelle spätestens die Beschreibung von Scott Draves (s.o.) runterladen. Dort findet Ihr dann auch noch grafische Beispiele zu den diversen 'variations'.
Viel Vergnügen beim Lesen, viel Erfolg beim Ausprobieren von Apophysis!

• Zum Seitenanfang