- Start Apophysis
- Teil 1: Transformeditor
- Teil 2: Skripteditor
- Teil 3: Üben mit dem Skripteditor
- Teil 4: Spiralform
- Teil 5: Transformeditor zu Skript
- mathematische Gedanken
- Startseite HP
Eine vollständige und allgemeinverständliche aktuelle Dokumentation - noch dazu in deutscher Sprache - konnte ich nirgends im Internet finden. Am übersichtlichsten ist meiner Meinung nach die Dokumentation von datagram (siehe Link Nr. 4 für den download), allerdings aus dem Jahr 2005 und in englischer Sprache. Links zu Anleitungen für die Verwendung von Apophysis findet ihr auf meiner Linkseite.
Diese Seite soll keine Dokumentation der Skriptsprache von Apophysis (Version 7X) sein, auch keine Anleitung für die Verwendung von Apophysis. Vielmehr möchte ich hier Anregungen geben, wie man sich selbst in die Skriptsprache einarbeiten kann und eigene Skripte schreiben (und testen) kann.
Am oberen Rand der Seite findet ihr Links zu gängigen Begriffen des Programmierens.
Ich beziehe mich bei meinen Beispielen auf die ff. Version:
|
Also fangen wir an: Klicke im Menü links auf Teil 1 / Transformeditor!
Erzeuge zunächst eine neue Datei (file / new / blank flame) und öffne dann den Editor (Transformeditor)(Menüpunkt ´view / editor´ oder Funktionstaste F4).
Es öffnet sich ein Fenster, in dem ein Dreieck OXY (in Apophysis ´transform´ genannt) zu sehen ist.
Gib ihm über den Menüpunkt ´colors´ eine Farbe deiner Wahl (über ´adjustment´/Funktionstaste F5 kannst du eine andere Farbpalette (gradient) wählen).
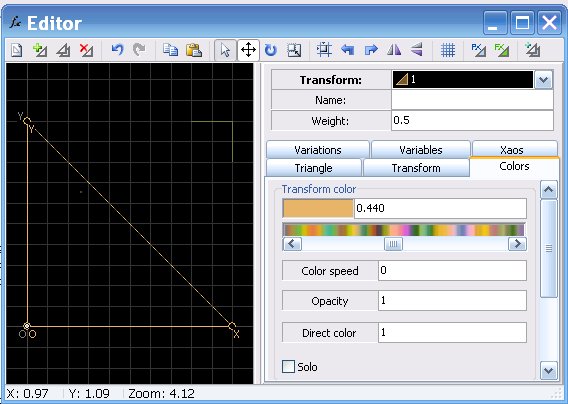
Mit gedrückter Maustaste auf der Ecke O kannst du das ganze Dreieck verschieben, mit gedrückter Maustaste auf den Ecken X und Y kannst du die Position dieser beiden Ecken verändern.
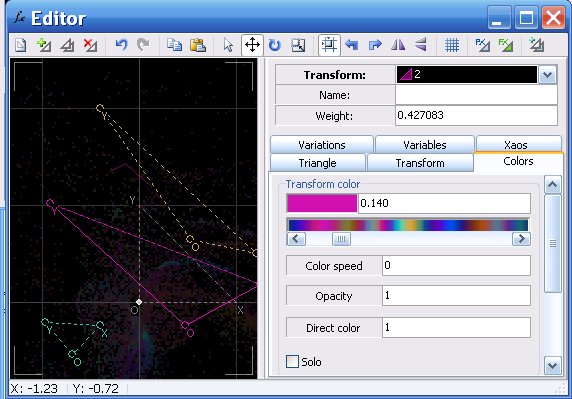
Füge nun noch 2 weitere Dreiecke hinzu (2. Menüpunkt oben von links),gib ihnen unterschiedliche Farben und ändere ihre Größen und Positionen. Falls nun im Apophysis-flame-Fenster nichts zu sehen ist, dann öffne über ´view / mutation´ oder mit der Funktionstaste F7 das Mutationsfenster und klicke mit der linken Maustaste solange auf das mittlere Feld, bis du etwas siehst:

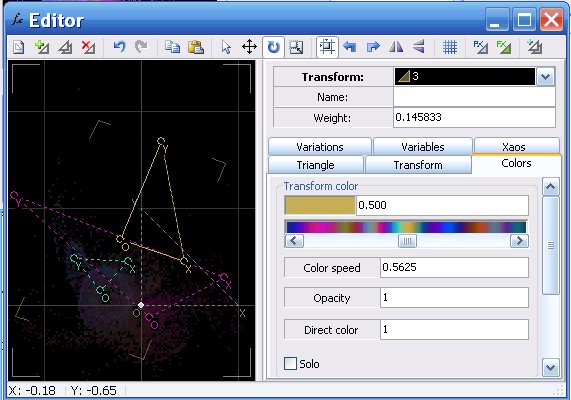
Jetzt ändere wieder mit der Maustaste Position und Größen der Dreiecke und beobachte, wie sich das Bild ändert. Bei Aktivierung von ´rotation mode´ (der 11. Menüpunkt von links) kannst du die Dreiecke auch drehen (auch ein Bewegungsmodus, ein Skalierungsmodus,.... ist vorhanden). Es muss jeweils oben rechts in der Auswahl das Dreick aktiviert sein, das du bearbeiten willst:

Als nächstes wollen wir die "Variationen" ausprobieren. Klicke auf ´variations´ und ändere dort die Werte, auch negative Zahlen kannst du ausprobieren, beobachte, wie sich das Bild ändert.
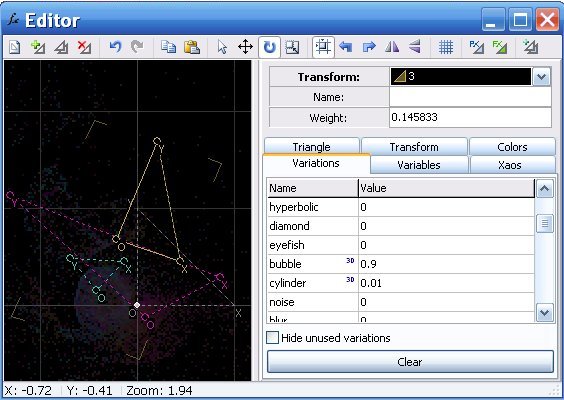

Füge weitere Dreiecke hinzu, ändere Farben, Positionen, Koordinaten ihrer Eckpunkte, ändere Variationen.
Und nachdem du genug experimentiert hast, wird es Zeit, ein kleines bisschen systematischer auf all dies zu schauen. Klicke im Menü links auf den 2. Teil!
Beginne wie im 1. Teil mit einer neuen ´flame´, öffne den Transformeditor, füge 3 Dreiecke in verschiedenen Farben ein und ändere deren Position, Größe und Form beliebig. Wähle nun im Menü ´Script´ den Befehle ´generate script from flame´. Es wird ein neues Fenster geöffnet, das das zur ´flame´ gehörende Skript zeigt. Bei meinem Beispiel:
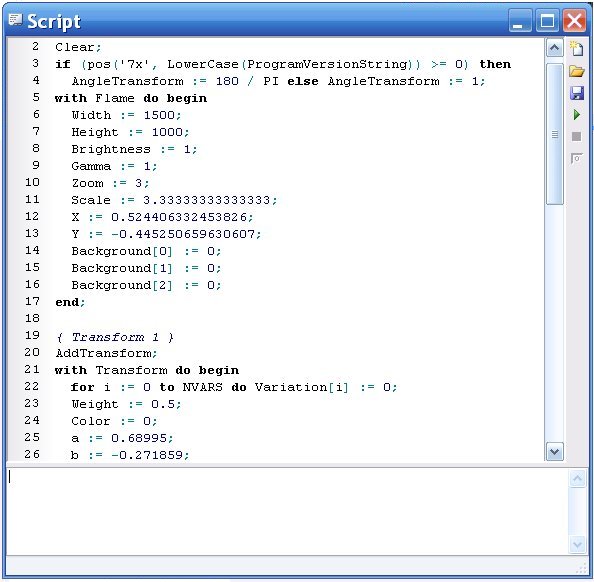
Im diesem vom Programm generierten Skript allerdings nicht erkennbar sind die Abbildungen, die man zuvor mit einem der Dreiecke gemacht hat, z.B. Rotationen, Verschiebungen, Skalierungen.
{ Flame }
Clear;
if (pos('7x', LowerCase(ProgramVersionString)) >= 0) then
AngleTransform := 180 / PI else AngleTransform := 1;
with Flame do begin
Width := 1500;
Height := 1000;
Brightness := 1;
Gamma := 1;
Zoom := 3;
Scale := 3.33333333333333;
X := 0.524406332453826;
Y := -0.445250659630607;
Background[0] := 0;
Background[1] := 0;
Background[2] := 0;
end;
Dieser erste Abschnitt betrifft allgemeine Informationen, du siehst, dass die Befehle mit einem Semikolon abgeschlossen werden. Lese an dieser Stelle auch die Zusatzinformationen am oberen Rand dieser Seite!
- Mit ´Clear´ werden alle Dreiecke (transforms) gelöscht, der Bildschirm wird leer, es müssen dann mindestens 2 neue Dreiecke erzeugt werden.
- In der ´if ... then ...else´- Abfrage wird festgelegt, ob Winkel im Bogenmaß oder Gradmaß verarbeitet werden.
- Zwischen den Schlüsselwörtern with flame do begin ... end; stehen sogenannte Wertzuweisungen:
Breite, Höhe, Helligkeit, Gammaschwellenwert, Zoom-Faktor, Skalierunge, x- und y-Position der (virtuellen) Kamera. Die drei Wertzuweisungen für Background geben den Farbanteil von ROT, GRÜN und BLAU an (0 bis 255). Laut Apoohysisscriting by datagram (2005 für ältere Versionen) werden die Farbanteile allein durch den ersten Wert festgelegt, Helligkeit und Intensität dann durch die nächsten Werte. Ändert man jedoch im Skript die Werte, dann stellt man fest, dass man die Farben mit den drei Werten mischen kann, jedoch in dieser Apophysis-Version keinerlei Einfluss auf Intensität und Helligkeit hat.
Ändere die Werte, gehe auf ´run script´ (kleiner grüner Pfeil) und sieh, was passiert. - X und Y geben an dieser Stelle die Positionierung der Kamera in x- und y-Richtung im Koordinatensystem an. Lieder wurden hier die gleichen Buchstaben wie für die Ecken des Dreiecks gewählt.
{ Transform 1 }
AddTransform;
with Transform do begin
for i := 0 to NVARS do Variation[i] := 0;
Weight := 0.5;
Color := 0.1;
a := 0.68995;
b := -0.271859;
c := -0.375377;
d := 0.958291;
e := 0;
f := 0;
Opacity := 0.011
linear3D := 1
end;
-
Der erste neue Befehl ist AddTransform;, eine Funktion, die ein neues Dreieck erzeugt, das dem Referenzdreieck entspricht. Gleichzeitig wird dieses Dreieck nun als aktiv definiert.
-
Neu ist außerdem die sogenannte Umgebungsvariable NVAR (Anzahl der ´variations´ in apophysis): Ihr Wert ist 18, ab Version_2_02 ist ihr Wert 22 laut Apophysisscripting by datagram aus dem Jahr 2005. Schaut man sich jedoch die ´settings´der Apophysis-Version 7X, auf die ich mich hier beziehe, an, dann sieht man, dass 52 mögliche ´variations´ eingebaut sind (die bei mir installierten plugins mitgezählt):
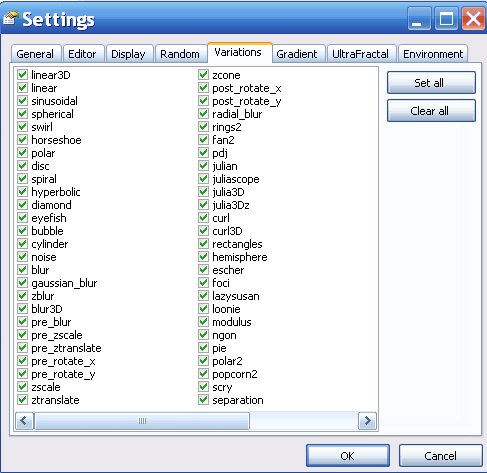
Die ´variations´ sind im Programm vordefinierte mathematische Funktionen, mit denen die Dreiecke (transforms) verändert werden.
Auch im Transform-Editor sind mögliche Variationen aufgelistet, dort sind es 56 Stück, wenn ich mich nicht verzählt habe.

Die ´variations´ sind in einen ´array´ gepackt (ein Datenfeld, eine Menge gleich strukturierter Daten) und werden über eine Indizierung aufgerufen: Variation[i].
In einer Zählschleife, die von 1 bis 22 läuft, wird den 22 "Schubladen" dieses Datenfeldes (array) der Wert 0 zugeordnet, sie werden also nicht angewendet. - Ändere nun den Wert für Weight (´weight´ ist ein Faktor, mit dem lt. Wikipedia die einzelnen Variationen, die auf eine der Flame-erzeugenden Funktionen angewendet werden, multipliziert werden, also eine Streckung vom Koordinatenursprung aus. Laut "scripting by datagram" aus dem Jahr 2005 wird die Summe aller ´weights´ auf 1 zurückskaliert, wie es in der Originasoftware von Scott Draves aus dem Jahr 1992 vorgeschlagen wurde. Dies in der vorliegenden Version lt. Wikipedia, s.o., nicht mehr der Fall.
Im Chaosspiel ist "Gewicht" die Wahrscheinlichkeit, mit der eine Abbildung eines IFS (Iteriertes Funktionensystem, iteratives Funktionensystem) gewählt wird, was v.a. dann eine Rolle spielt, wenn die Abbildungen nicht gleich stark kontrahieren. Die schwächer kontrahierende Abbildung verteilt ihre Punkte auf eine größere Fläche, sodass der Anschein von Transparenz entsteht.
Andere auch die Werte für Color (von 0 bis 1, andere Werte werden von Apophysis verworfen), Opacity und linear3D und beobachte die Veränderung (Doppelklick im Transformeditor ändert von 0 auf 1 und zurück). - Die Variablen a bis f sind die Koordinaten der Ecken X, Y und O des Dreiecks:
X(a/b), Y(c/d) und O(e/f).
Im Transformeditor: Beim Menüpunkt ´triangle' können die Koordinaten für die Ecken des Dreiecks eingegeben werden. Beim Menüpunkt 'transforms' können die Dreiecksseiten OX und OY skaliert werden (anscheinend ist das Zentrum die Ecke O), die Ecke O kann verschoben werden. Wird z. B. die Ecke O um 2 Einheiten nach oben geschoben, dann erscheint bei der y-Koordinate der Ecke X der negative Wert -2, falls dort vorher eine Null stand. Ich hoffe, ich habe das so richtig verstanden, die diversen Anleitungen zum Erstellen von `flames` sind nicht immer sehr klar. Die jeweiligen Autoren haben diese flames nicht mit Scripting erstellt. Sollte mir irgendwann ein neues Licht aufgehen, dann werden ich dies hier ändern.
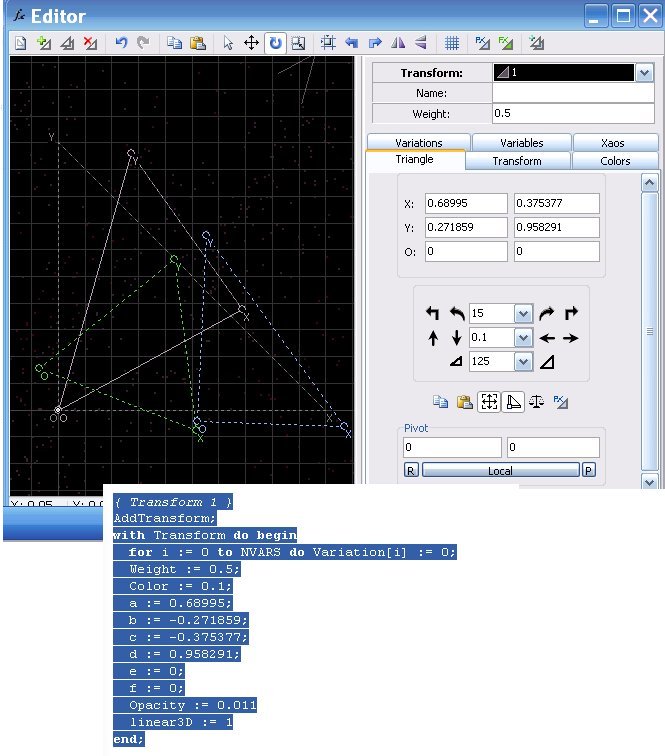
Ändere im Skripteditor die Werte für a bis f, und beobachte die Veränderungen im Transformeditor und auch bei der ´flame´.
Abschnitt 3 und 4 des Skriptes sind analog zu obigem Abschnitt mit entsprechend abgeänderten Koordinaten der jeweiligen Dreiecke.
Ein bisschen Übung kann nicht schaden:
Schreiben wir mal ein Startskript mit einer Zählschleife und klicken auf ´run´. Im Transformeditor können wir sehen, was geschieht:
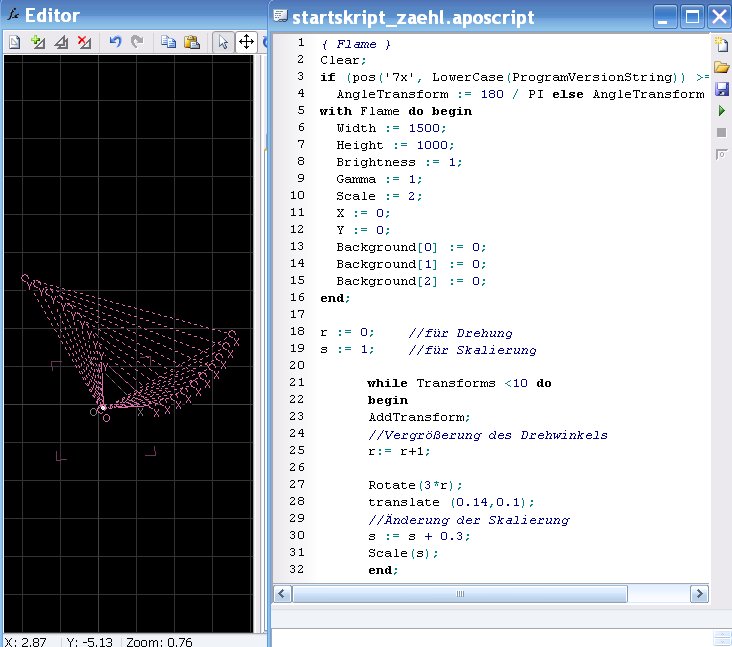
Im ersten Teil des Skripts werden die allgemeinen Eigenschaften festgelegt (siehe vorh. Kapitel), im zweiten Teil werden zunächst 2 Variable r und s definiert, die dann für Rotation und Skalierung benutzt werden, dann werden 10 Dreiecke (Nr. 0 bis Nr. 9) erzeugt.
Der Rotationswinkel wird dann um 1 vergrößert, anschließend wird das Dreieck um das 3-fache von r (in Grad) rotiert. Es wird dann um (x,y) verschoben. Die Skalierung wird nun ebenfalls geändert, das Dreieck dann mit dem Faktor s gestreckt von seiner Ecke O aus.
Ändere nun das Skript (Rotation, Skalierung, Zahl der Dreiecke) und beobachte im Transformeditor, was geschieht.
Es ist nun einsichtig, dass die Skripte schlichtweg aus Befehlen bestehen, mit deren Hilfe man sich die Klickerei im Transformeditor sparen/erleichtern kann, insbesondere dann, wenn ein Befehl sehr oft (Zählschleife) ausgeführt werden soll.
Spiralform
Bei Link Nr. 5 (vgl. oberer Seitenrand) gibt es eine Anleitung zur Erstellung einer Spirale Posted by UltraGnosis in Basic, diese Spirale wird mit dem Transformeditor erzeugt. In etwas veränderter Form gebe ich diese Anleitung hier wieder:
In diesem Abschnitt erzeugen wir zunächst mit dem Transformeditor eine Spirale und versuchen dann, dieselbe Spirale mit Hilfe eines geeigneten Skript zu erzeugen.
- Öffne den Transformeditor, wähle ´new flame´ und setze bei ´variations´ linear3D auf 0.1
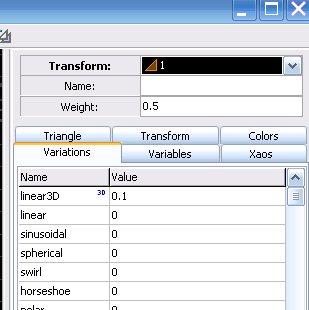
- Füge nun ein 2. Dreieck (geeignete Farbe wählen) hinzu und wähle weight=10.
- Schiebe das Dreieck eine Einheit nach rechts.
- Rotiere es um 15 Grad gegen den Uhrzeigersinn.
- Setze den Skalierungsfaktor auf 101 und klicke auf das kleine Dreieck links neben dem Skalierungsfeld, um es auf 99% zu verkleinern.
- Falls im Hauptfenster nicht zu sehen ist, dann öffne den Adjustmenteditor stelle für die Kamera einen geeigneten Zoomfaktor ein, im Hauptfenster kann du dann mit gedrückter linker Maustaste das Bild zurechtrücken.
- Über den Menüpunkt ´colors´ kannst du auch noch die Farben verändern.
- Für das Skript: Im Adjustment-Editor kannst Du nun auch Zoom und Kameraposition ablesen.
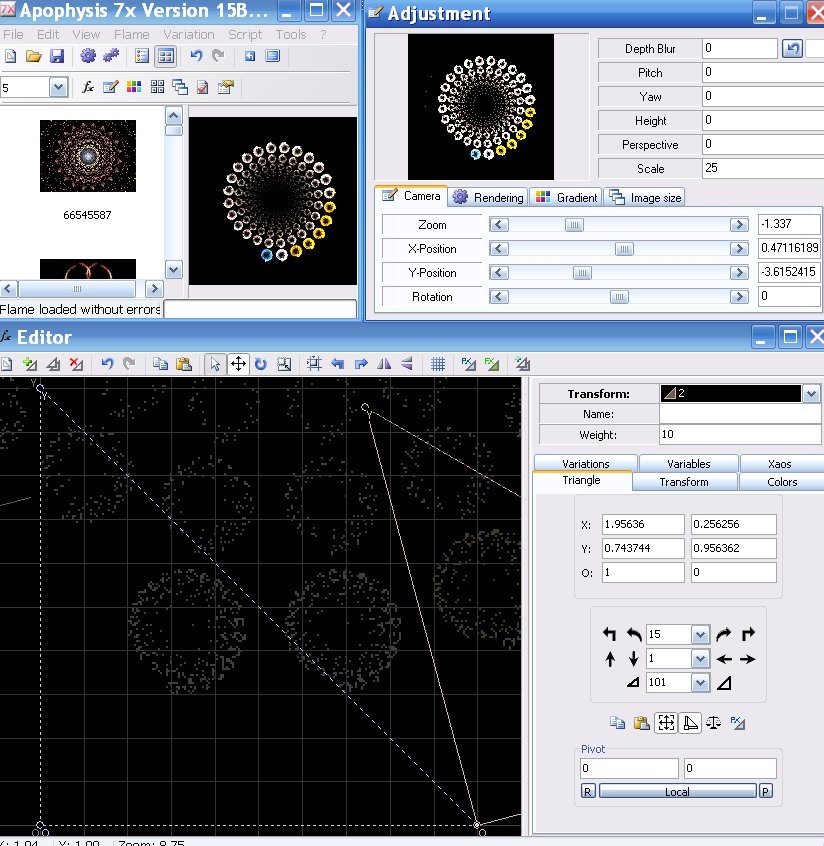
Beim Schreiben des Skripts wollen wir es uns nicht allzu schwer machen: Wir wählen nun im Hauptmenü den Punkt ´script/generate script from flame´ und sehen uns das mal an:
{ Flame }
Clear;
if (pos('7x', LowerCase(ProgramVersionString)) >= 0) then
AngleTransform := 180 / PI else AngleTransform := 1;
with Flame do begin
Width := 300;
Height := 300;
Brightness := 9.9;
Gamma := 1;
Zoom := -1.337;
Scale := 25;
X := 0.471161899062085;
Y := -3.61524154186026;
Background[0] := 0;
Background[1] := 0;
Background[2] := 0;
end;
{ Transform 1 }
AddTransform;
with Transform do begin
for i := 0 to NVARS do Variation[i] := 0;
Weight := 0.5;
Color := 0.64;
a := 1;
b := 0;
c := 0;
d := 1;
e := 0;
f := 0;
Opacity := 1
linear3D := 0.1
end;
{ Transform 2 }
AddTransform;
with Transform do begin
for i := 0 to NVARS do Variation[i] := 0;
Weight := 10;
Color := 0.529;
Symmetry := 0.98;
a := 0.956362;
b := 0.256256;
c := -0.256256;
d := 0.956362;
e := 1;
f := 0;
Opacity := 1
linear3D := 1
end;
Im ersten Teil erkennen wir einige unserer Einstellungen: Die Bildgröße (ich hatte sie tatsächlich auf 300x300 eingestellt), Helligkeit, Gammafaktor, Zoom und Kameraposition stimmen mit den Werten im Adjustment-Editor überein.
Auch die Einstellung für das Referenzdreieck (Farbe, Gewicht, linear3D=0.1) sind im 2. Teil des Skripts ablesbar.
Auch weight=10 und Farbe sind noch im 3. Teil des Skripts erkennbar.
Was jedoch ist mit Verschiebung (1 Einheit nach rechts), Drehung (15 Grad gegen den Uhrzeigersinn) und Skalierung geschehen? Davon ist hier nichts mehr ablesbar, all diese Werte stecken in den Koordinaten des 2. Dreiecks. Wenn man diese nun vorsichtig ändert, ändert sich die ´flame´ möglicherweise gravierend. Wir haben die Kontrolle verloren.
Also ändern wir den 2. Teil des Skripts: Zunächst nehmen wir für die Dreieckskoordinaten wieder die Koordinaten des Referenzdreiecks.
Und nun schreiben wir genau das in Skript, was wir im Transformeditor getan hatten: Um eine Einheit nach rechts schieben, 15 Grad rotieren und dann auf 99% skalieren.
Der letzte Skriptteil sieht nun wie folgt aus:
{ Transform 2 }
AddTransform;
with Transform do begin
for i := 0 to NVARS do Variation[i] := 0;
Weight := 10;
Color := 0.529;
Symmetry := 1;
a := 1;
b := 0;
c := 0;
d := 1;
e := 0;
f := 0;
translate (1,0);
rotate (15);
scale (0.99);
Opacity := 1
linear3D := 1
end;
Speichern wir das Skript und wählen ´run´, dann sehen wir, dass es wieder unsere ´flame´ erzeugt! Wir haben die Kontrolle zurückgewonnen!
... und zur Übung werden nun die Werte für das 2. Dreieck geändert. Anschließend kann man an dieser Stelle auch noch ´variations´ einfügen und mit ein bisschen Glück entstehen ansehbare ´flames´.
Noch ein Minibeispiel:
{ Transform 2 }
AddTransform;
with Transform do begin
for i := 0 to NVARS do Variation[i] := 0;
Weight := 10;
Color := 0.529;
Symmetry := 0.98;
a := 1;
b := 0;
c := 0;
d := 1;
e := 0;
f := 0;
translate (1.31,0.3);
rotate (31);
scale (0.99);
Opacity := 1
linear3D := 1
hyperbolic := -0.03
bubble := -0.12
end;
...in Kombination mit geeignetem Zoom und geeigneter Kameraposition gibt´s ´ne Art fraktalen Weihnachtsbaum, nicht wirklich schön aber einzigartig.
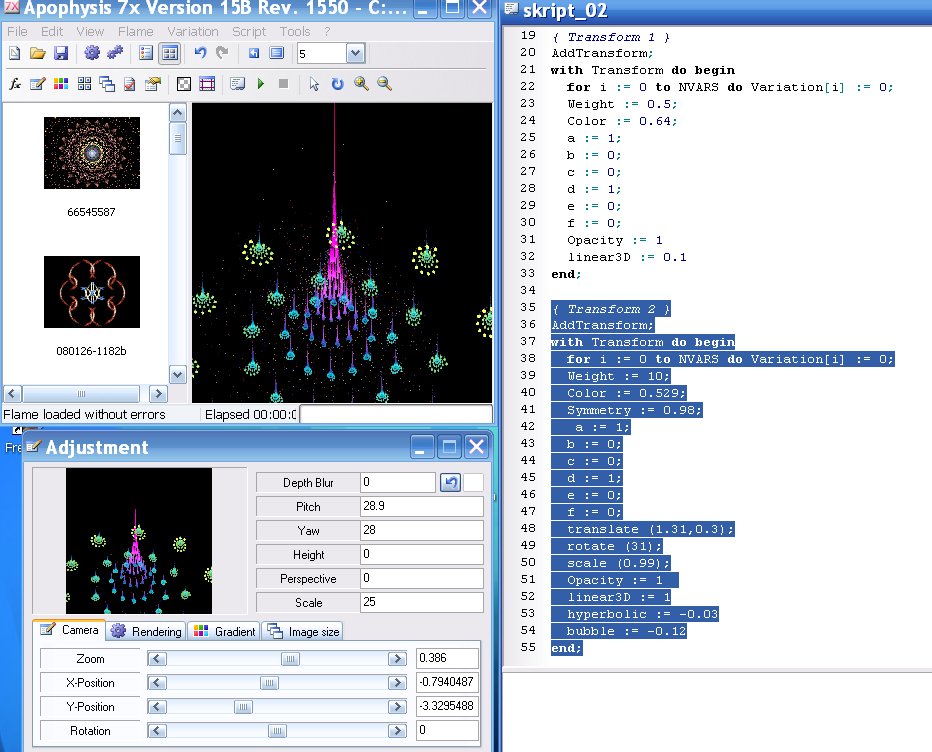
Zum Abschluss noch ein kommentiertes Skript mit Zählschleife und FinalTransform (auf alle Dreiecke werden bestimmte ´variations´ angewendet). Das Ergebnis ist zumindest ´ne Ecke schöner als der fraktale Weihnachtsbaum:
{ Flame }
Clear;
if (pos('7x', LowerCase(ProgramVersionString)) >= 0) then
AngleTransform := 180 / PI else AngleTransform := 1;
with Flame do begin
Width := 300;
Height := 500;
Brightness := 9.9;
Gamma := 3;
Zoom :=0.8;
Scale := 30;
X := 0.7;
Y := -0.1;
Background[0] := 0;
Background[1] := 0;
Background[2] := 0;
end;
{ Transform 1 / Referenzdreieck }
AddTransform;
with Transform do begin
for i := 0 to NVARS do Variation[i] := 0;
Weight := 0.15;
Color := 0.64;
a := 1;
b := 0;
c := 0;
d := 1;
e := 0;
f := 0;
Opacity := 1
linear3D := 0.1
end;
{ Transform bis Nummer 3, d.h. 4 Stück }
AddTransform;
with Transform do begin
for i := 0 to NVARS do Variation[i] := 0;
r := 0; //für die Drehung
s := 1; //für die Skalierung
while Transforms < 5 do
begin
weight:= 0.01;
linear3D := 0.484;
AddTransform;
translate (0.1,0.1)
r := r+5; //r vergrößern
Rotate(r*0.75); //rotieren
s := s - 0.075; //s vergrößern oder verkleinern
Scale(s); //skalieren
Transform.curl:= 0.16; //für alle Dreiecke
//einfärben mit versch. Farben:
for j:= 0 to Transforms - 1 do begin
SetActiveTransform(j);
Transform.Color := j /(Transforms - 1)/1.6;
end //Ende färben
end; //Ende while-Schleife
end; //Ende Transform-Schleife
//für das 4. Dreieck Variationen wählen:
SetActiveTransform(3);
with Transform do begin
Transform.curl:= 0.16;
Transform.swirl:= 0.16;
end;
//für die komplette Flamme:
{ Final Transform }
SetActiveTransform(transforms);
with Transform do begin
Transform.weight := 0.01
Transform.escher :=0.85
end;
Transformeditor zu Skript
Bei den tutorials im JPG-Format bei deviantart findet sich ein spherical-tutorial von Fiery-Fire in französischer Sprache. Auch in englischer Sprache ist es vorhanden.
In leicht abgewandelter Form soll hier das Skript für die ersten 5 Dreiecke (transforms) dazu entwickelt werden.
Die ersten 5 Dreiecke sehen folgendermaßen aus (im Koordinatenursprung die Ecke O des Referenzdreiecks, mit Seite OX nach rechts und Seite OY nach oben weisend):
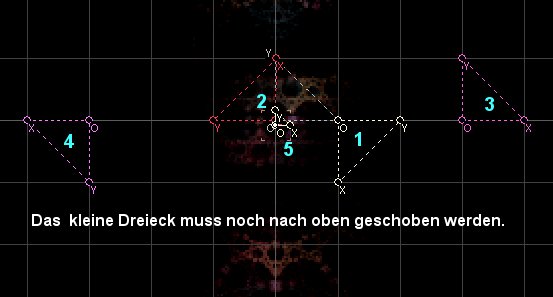
- Nummer 1 ist um 90 Grad im Uhrzeigersinn gedreht, was einer Drehung um 270 Grad gegen den Uhrzeigersinn entspricht. Anschließend wurde es um 1 Einheit nach rechts verschoben.
translate (1,0); rotate (270); - Nummer 2 ist einfach um 90 Grad gegen den Uhrzeigersinn gedreht.
rotate (90);
-
Nummer 3 entspricht dem um 3 Einheiten nach rechts geschobenen Referenzdreieck:
translate (3,0);
-
Nummer 4: Das Referenzdreieck wird 3 Einheiten nach links geschoben, dann um 180 Grad um seine Ecke O gedreht. An dieser Stelle die Bermerkung, dass Drehung und Verschiebung i.a. nicht kommutativ (=vertauschbare Reihenfolge) sind.
Dreht man dieses Dreieck zuerst und verschiebt es dann um 3 Einheiten nach links, dann rutscht es nach rechts, in diesem Beispiel unverständlich, da Rotation nicht den Koordinatenursprung sondern die Ecke O als Zentrum hat (Zumindest, wenn man Im Skripteditor ein bereits verschobenes Dreieck dreht, sieht man, dass dann nicht die in der Geometrie übliche Drehung um den Koordiantenursprung benutzt wird. Zum Drehzentrum konnte ich in keiner Dokumentation einen Hinweis finden.).
translate (-3,0); rotate (180);
-
Nummer ist ist verkleinert und nach oben geschoben, der y-Wert der Ecke O als negative Zahl eingegeben, da es sich sonst nach unten schiebt.
Transform.A := 0.239392; Transform.B := 0; Transform.C := 0; Transform.D := 0.239392; Transform.E := 0; Transform.F := -0.085;
Bei der Verschiebung der Ecke O nach oben, sieht man dann, dass sich auch die Koordinaten der Ecke Y des Dreiecks ändern:
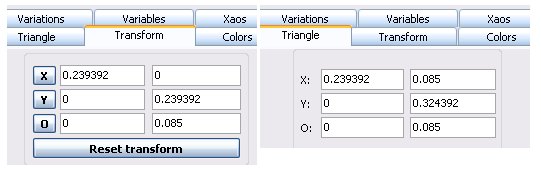
Hier eine Bemerkung zum Transformeditor/Skripteditor: Schreibt man translate (1,1), so schiebt sich das Dreieck nach UNTEN, statt nach oben, was darauf hin weist, dass die positive y-Achse nach unten weist, während die positive x-Achse jedoch nach rechts weist. In keiner Internet-Dokumentation der Befehle habe ich einen derartigen Hinweis gefunden.
Fügt man nun die die Angaben für weight und für variations von Fiery-Fire ein und auch die gewünschten Farben, dann erhält man das folgende Skript und ein ähnliches Bild wie das im Internet vorgestellte (bei meiner Version ist linear:= 0 statt linear:= 1 ab Nummer 3!):
{ Flame }
Clear;
if (pos('7x', LowerCase(ProgramVersionString)) >= 0) then
AngleTransform := 180 / PI else AngleTransform := 1;
with Flame do begin
Flame.Name:= 'spherical_script'
Width := 500;
Height := 500;
Brightness := 0.95;
Gamma := 1;
Zoom := 3;
Scale := 20;
X := 0.4;
Y := -0.04;
Background[0] := 0;
Background[1] := 0;
Background[2] := 0;
end;
{Nummer 1}
AddTransform;
Transform.Weight:=7;
Transform.linear3D:= 0;
Transform.linear:= 0;
Transform.spherical := 1;
translate (1,0);
rotate (270);
Transform.symmetry:= 0.95;
Transform.color:= 0.38;
{Nummer 2}
AddTransform;
Transform.Weight:=7;
Transform.linear3D := 0;
Transform.linear:= 0;
Transform.spherical:= 1;
rotate (90);
Transform.symmetry:= 0.95;
Transform.color:= 0.228;
{Nummer 3}
AddTransform;
Transform.Weight:=0.35;
Transform.linear3D := 0;
Transform.linear:= 0;
Transform.spherical:= 1;
translate (3,0);
Transform.color:= 0.350;
{Nummer 4}
AddTransform;
Transform.Weight:=0.35;
Transform.linear3D := 0;
Transform.linear:= 0;
Transform.spherical:= 1;
translate (-3,0);
rotate (180);
Transform.color:= 0.660;
{Nummer 5}
AddTransform;
weight:= 0.05;
Transform.linear3D := 0;
Transform.linear:= 0;
Transform.eyefish := 0.01;
Transform.bubble:= 0.35;
Transform.symmetry:= -0.45;
//Koordinaten transformieren
Transform.A := 0.239392;
Transform.B := 0;
Transform.C := 0;
Transform.D := 0.239392;
Transform.E := 0;
Transform.F := -0.085;
Transform.color:= 0.670;

Die weiteren transforms, die Fiery-Fire zur Verfeinerung seiner flame einfügt, könnt ihr nun selbst ergänzen.