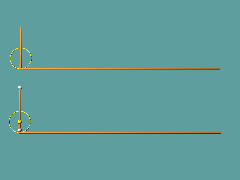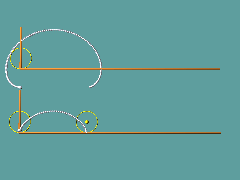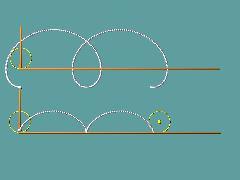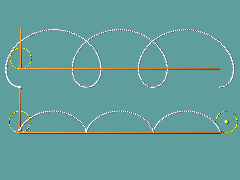Gewöhnliche, verkürzte und verlängerte Zykloiden
Rollt ein Kreis auf einer Geraden ab, so kann man die Bahnkurve eines Punktes auf der Kreislinie beobachten: Der Punkt Q falle zunächst mit dem Nullpunkt N des Koordinatensystems zusammen.
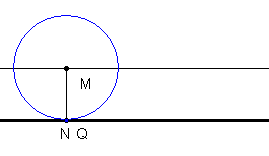
M bewege sich dann mit gleichförmiger Geschwindikeit parallel zur x-Achse, entsprechend rollt Q auf der Kreislinie mit: Es entsteht eine gewöhnliche Zykloide.
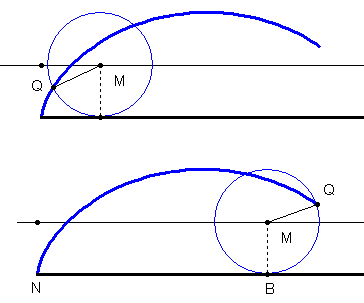
Bemerkung zur Namensgebung:
Liegt der zu beobachtende Punkt auf der Kreislinie des abrollenden Kreises, so spricht man von einer gewöhlichen Zykloiden, die Bezeichnung verkürzte Zykloide wird dann für die Bahnkurve eines Punkten benutzt, dessen Abstand a vom Kreismittelpunkt kleiner als der Radius ist, eine verlängerte Zykloide liegt vor, wenn a > r ist.
Herleitung der Bahnkurve:
Bahnkurve von Q einer gewöhnlichen Zykloide: in Abhängigkeit vom Drehwinkel

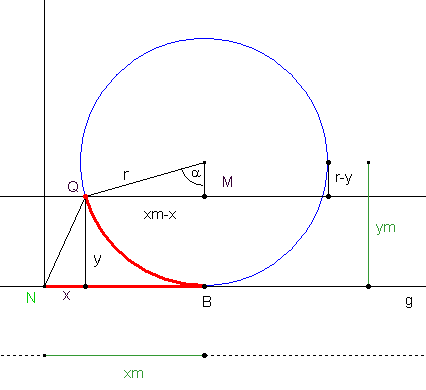
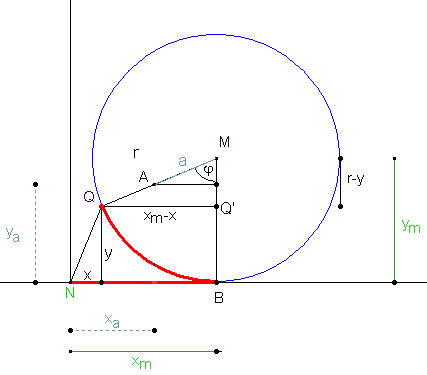
In der Startposition des Kreises falle der Punkt B mit dem Nullpunkt N zusammen. Beginnt der Kreis auf der Geraden g abzurollen, so entspricht die Länge des Kreisbogens BQ gleich der Strecke BN bzw. der x-Koordinate x m des Kreismittelpunktes M.

Der Quotient aus Kreisbogen und Vollwinkel ist also gleich dem Quotienten aus  und 360°:
und 360°:
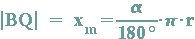
Es gilt also (vgl. die Abbildung oben):
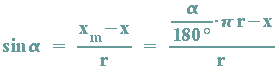 und
und
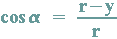
Löst man die 2. Gleichung nach r auf, dann erhält man:
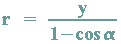
Setzt man nun das Ergebnis in die 1. Gleichung ein, so ergibt sich:
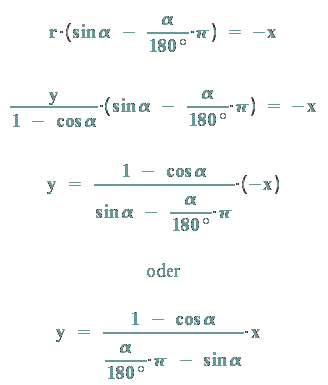
Bahnkurve einer gewöhnlichen Zykloide: in Abhängigkeit der Winkelgeschwindigkeit
Aus

und
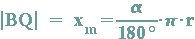
und der Umrechnungsformel von Grad zu Bogenmaß
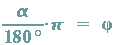
folgt, dass der Abstand des Berührpunktes B vom Nullpunkt N gleich dem Produkt aus 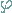 und dem Radius r ist:
und dem Radius r ist:
Es gilt also:

Für die x-Koordinate von Q gilt:
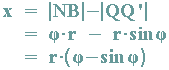
Für die y-Koordinate von Q gilt:
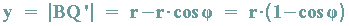
Betrachten wir nun nicht den Punkt Q(x/y) auf der Kreislinie sondern den Punkt A(xa/ya), der im Kreisinnern oder außerhalb des Kreises liegt und den Abstand a zum Kreismittelpunkt hat, dann gilt (vgl. Abbildung):
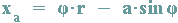
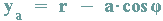
Setzt man in den beiden letzten Formeln a=r, so ergeben sich wieder die Formeln für die Koordinaten von Q(x/y).
Bahnkurve einer gewöhnlichen Zykloide: Parameterdarstellung
Das Abrollen eines Kreises auf einer Geraden ist aus 2 Bewegungen zusammengesetzt:
Eine geradlinige Bewegung mit gleichförmiger Geschwindigkeit des Kreismittelpunktes M(xm/r) parallel zur x-Achse (Translation) und der Rotation des Kreises.
Zur Herleitung der Bahngleichung kann also auch das Superpositionsprinzip benutzt werden:
Für die Translationsbewegung von M gilt:
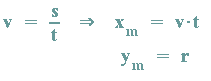
Für die Rotationsbewegung von Q(xr)/yr)) gilt:
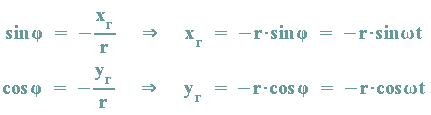
Für beide Bewegungen addieren sich nun die Koordinaten in Abhängigkeit von der Zeit t:
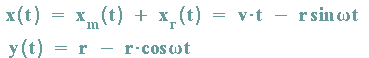
Was hier noch stört, ist die Geschwindigkeit v des Kreismittelpunktes M.
Für v gilt:
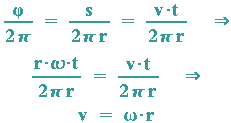
Dies wird in die Bahngleichungen eingesetzt und in vektorieller Form erhält man:
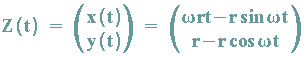
| © 2009 Asti | Links für Unterricht | PoVRay-Site |