Das Möbiusband

Im Jahr 1865 veröffentlichte Professor August Ferdinand Möbius das bekannte Möbiusband: eine 3-dimensionale endliche Fläche mit nur einer Seite und nur einem Rand. Verdreht man einen Papierstreifen um 180° und klebt die beiden Ende zusammen, dann erhält man ein Möbiusband.

Am Ende dieser Seite sind Links zu entsprechenden Videos im Internet aufgeführt.



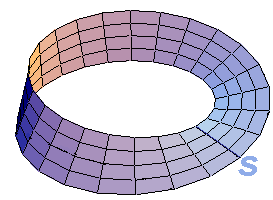
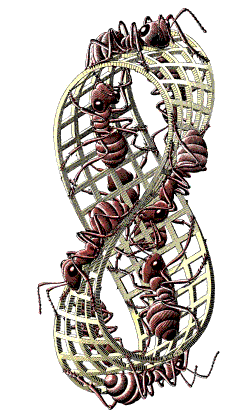
Bekannt ist das Bild des niederländischen Graphikers Maurits Cornelius Escher (1898-1972) mit den über ein Möbiusband laufenden Ameisen:

Auch ein Möbiusband entsteht durch Bewegung:

Bei Mausklick auf die jeweilige Abbildung wird der Programmiertext angezeigt.

Zunächst bewegt sich eine Strecke, deren Länge der Breite des Bandes entspricht auf einer Kreislinie:



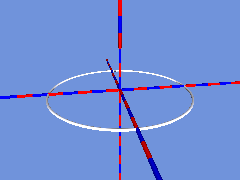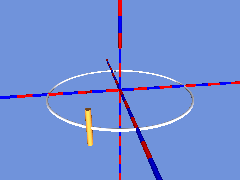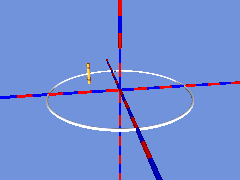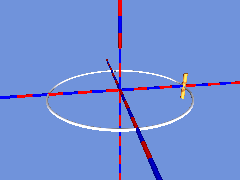
Setzt man an jede Position einen Zylinder, so hat man schon fast ein Band, das allerdings nicht um 180° verdreht zusammengefügt ist:



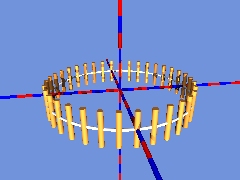
Es müssen nur noch die Zylinder dichter gesetzt werden:



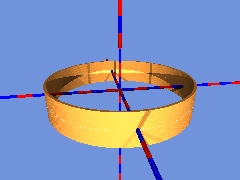
Dreht sich nun der in Kreis laufende Zylinder so um seinen Mittelpunkt, dass er sich bei einer Volldrehung um 180° gedreht hat, dann kann die Entstehung des Möbiusbandes aus der Bewegung einer Strecke nachvollzogen werden:




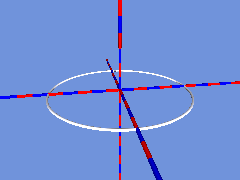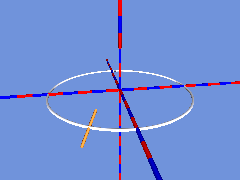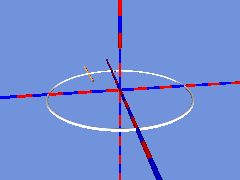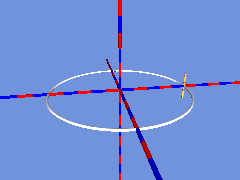
Als nächstes wird nun wieder an jede Position ein Zylinder gesetzt:



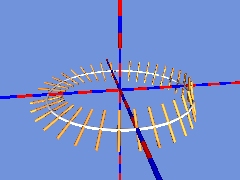
Wieder wird der Abstand der Zylinder verkleinert, sodass nun ein Möbiusband entsteht:

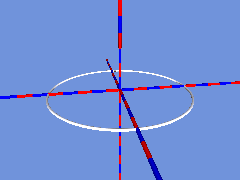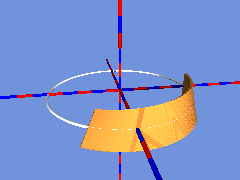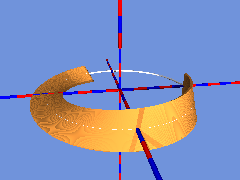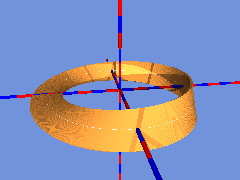
Dreht sich die bewegte Strecke beim Durchlaufen des Kreises nicht um das 1-fache von 180°, sondern um ein geradzahliges Vielfaches von 180°, dann entsteht kein Möbiusband, sondern eine doppelseitige Fläche, die man auch zweifarbig einfärben kann:

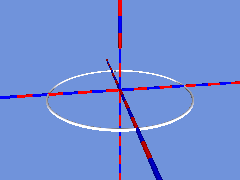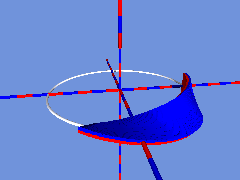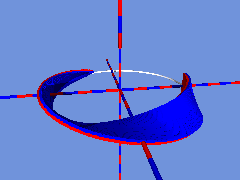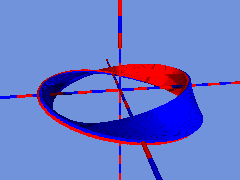
Links im Internet:

Video: Herstellung und Zerschneiden eines Möbiusbandes
Video: Zerschneiden eines Möbiusbandes
Video: Transformationen auf einem Möbiusband:
Video: Ein gestricktes Möbiusband - in engl. Sprache