Trochoiden und Zykloiden
Die Idee stammt aus dem Bewegungsmodul der sehr sehenswerten Matheprisma-Seite der Uni Wuppertal.
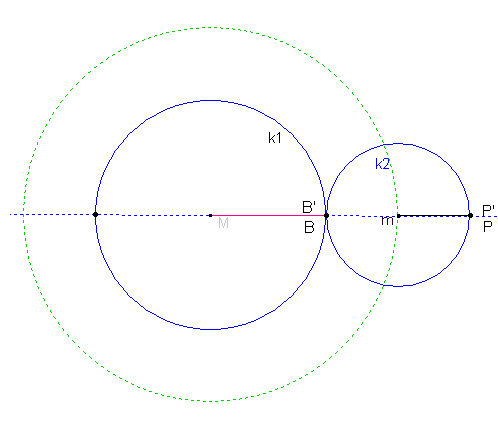
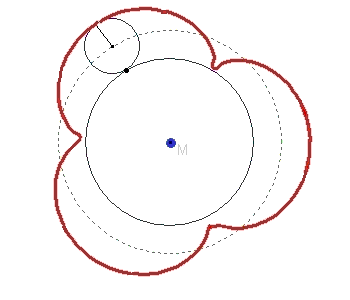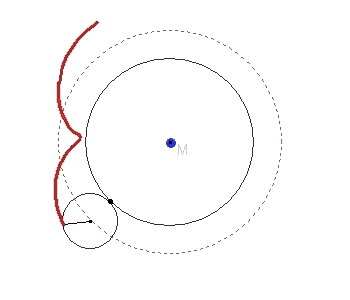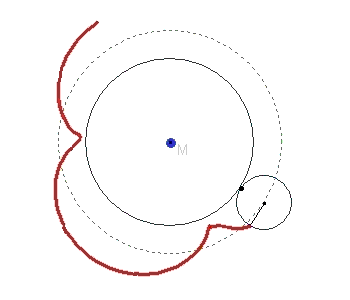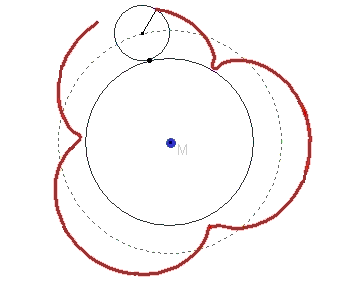
Zeichnet man zwei Kreise, die einander berühren und lässt die Kreislinie des einen auf der anderen abrollen, so muss man sich nur noch einen Punkt auf oder in der Nähe der kleinen Kreislinie denken, der mit rotiert, und schon ergibt dessen Ortslinie
eine TROCHOIDE. Der in der Abbildung äußere Kreis kann auch im Innern des Ausgangskreises abrollen.
Bemerkung zur Namensgebung:
Liegt der zu beobachtende Punkt auf der Kreislinie des abrollenden Kreises, so wird die Bahnkurve oft als Zykloide bezeichnet, die Bezeichnung Trochoide wird dann für Bahnkurven von Punkten benutzt, die innerhalb oder außerhalb des abrollenden Kreises liegen.
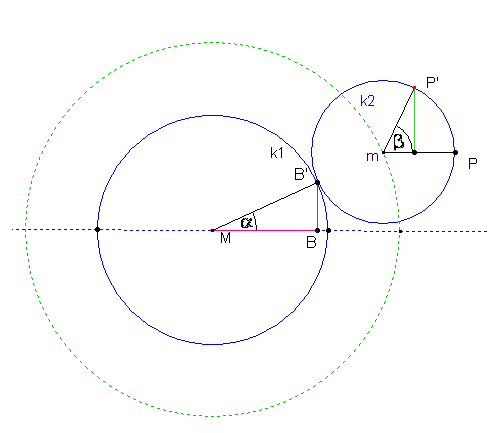
Rollt der kleine Kreis gegen den Uhrzeigersinn auf der Kreislinie des großen ab, dann bewegt sich P auf dem kleinen Kreis nach P'. Um dieselbe Kreisbogenlänge ist dann der Berührpunkt B der beiden Kreise auf dem großen Kreis gegen den Uhrzeigersinn gewandert. Der neue Berührpunkt sei dann B'.
Die Bogenlängen PP' und BB' sind gleichlang.
Um die Linie, auf der der Punkt P sich bewegt, genauer untersuchen zu können, suchen wir zunächst einen Zusammehang
zwischen den Winkeln  und ß und beachten dabei die gleiche Länge der genannten Kreisbögen.
und ß und beachten dabei die gleiche Länge der genannten Kreisbögen.
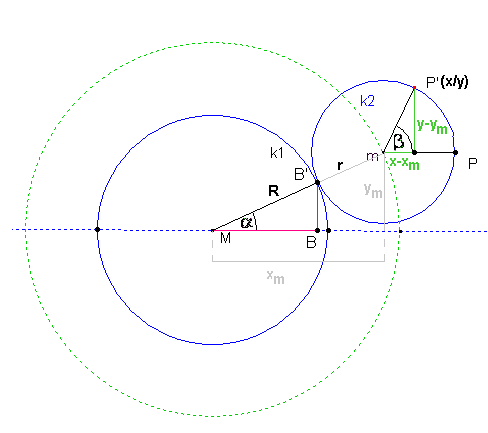
Anhand der letzten Abbildung erkennt man nun die folgenden Zusammenhänge:
Für die beiden Kreisumfänge gilt:

Für die Kreisbögen gilt dann:
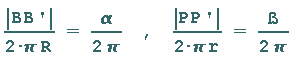
Da beide Kreisbögen gleichlang sind, folgt daraus:
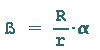
Anhang der 3. Abbildung erkennt man, dass:
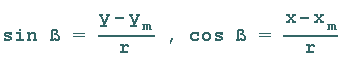
Woraus die Gleichungen für die Koordinaten von P(x/y) folgen:

Programmiert man nun eine solche Ortslinie, dann können die Werte für R und r frei gewählt werden
(negative Werte für r bewirken, dass der kleine Kreis innerhalb des großen Kreises abrollt).
Ein programmiertes Beispiel:

Der Programmcode wurde mit PoVRay erstellt.
#macro Mache_rahmen (Aussenradius)
union{
#local R_gross=Aussenradius;
#local R_klein=R_gross/15;
#local faktor=1/255;
#declare Alpha=.1;
#while (Alpha<360.05)
#declare Beta= R_gross/R_klein*Alpha;
#declare xm=(R_gross+R_klein)*cos(Alpha);
#declare ym=(R_gross+R_klein)*sin(Alpha);
//Der Punkt P muss nicht auf der kl. Kreislinie liegen!
//verändert xm und ym!
#declare X=R_klein*cos(Beta)+xm;
#declare Y=R_klein*sin(Beta)+ym;
sphere{<X,Y,0>,.075//Der Kugelradius bestimmt die Rahmendicke
pigment {color rgb<148,199,222>*faktor}
finish{F_MetalA}
}//ende kugel
#declare Alpha=Alpha+0.25;
#end //end while
}//end union
#end //Ende des Makros
Mache_rahmen(3.1) //Makro aufrufen
Entstehung von Trochoiden
Die folgende GIF-Animation zeigt die Entstehung einer Trochoide beim Abrollen eines kleinen Kreises auf einer großen Kreislinie.
|
| © 2009-2024 Asti | PoVRay-Site |