Trochoids and cycloids
The idea comes from the motion module of the very interesting Matheprisma page of the University of Wuppertal.
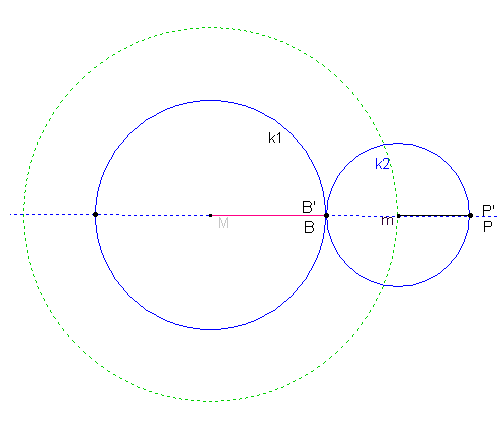
If you draw two circles that touch each other and let the circle line of one roll on the other, you only have to think of a point on or near the small circle line that also rotates, and its location line
will result in a TROCHOIDE. The outer circle in the illustration can also roll inside the initial circle.
Comment on the naming:
If the point to be observed lies on the circular line of the rolling circle, the trajectory is often referred to as a cycloid, the term trochoid is then used for trajectories of points that lie inside or outside the rolling circle.
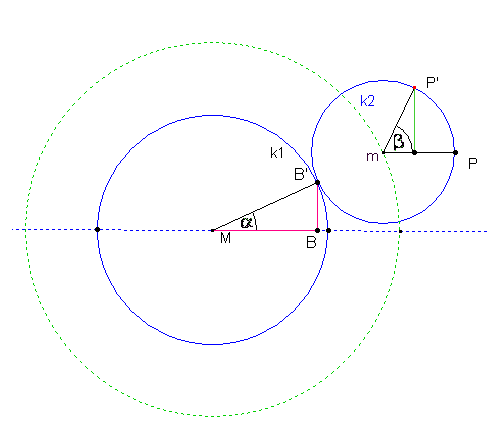
If the small circle rolls counterclockwise on the circular line of the large circle, then P moves on the small circle to P'. The point of contact B of the two circles on the large circle has then moved anticlockwise by the same arc length. The new point of contact is then B'.
The arc lengths PP' and BB' are the same length.
In order to be able to examine the line on which the point P moves more closely, we first look for a connection
between the angles  and ß and note the same length of the circular arcs mentioned.
and ß and note the same length of the circular arcs mentioned.
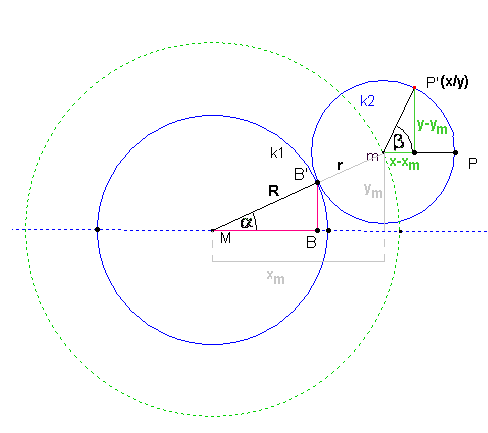
The last figure shows the following relationships:
The following applies to both circumferences:

The following then applies to the circular arcs:
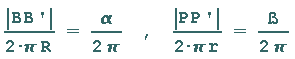
Since both arcs are the same length, this follows:
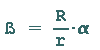
Appendix of the 3rd figure shows that:
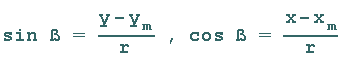
From which the equations for the coordinates of P(x/y) follow:

If you now program such a locus line, the values for R and r can be freely selected
(negative values for r cause the small circle to roll inside the large circle).
A programmed example:

The program code was created with PoVRay.
#macro Mache_rahmen (Aussenradius)
union{
#local R_gross=Aussenradius;
#local R_klein=R_gross/15;
#local faktor=1/255;
#declare Alpha=.1;
#while (Alpha<360.05)
#declare Beta= R_gross/R_klein*Alpha;
#declare xm=(R_gross+R_klein)*cos(Alpha);
#declare ym=(R_gross+R_klein)*sin(Alpha);
//Der Punkt P muss nicht auf der kl. Kreislinie liegen!
//verändert xm und ym!
#declare X=R_klein*cos(Beta)+xm;
#declare Y=R_klein*sin(Beta)+ym;
sphere{<X,Y,0>,.075//Der Kugelradius bestimmt die Rahmendicke
pigment {color rgb<148,199,222>*faktor}
finish{F_MetalA}
}//ende kugel
#declare Alpha=Alpha+0.25;
#end //end while
}//end union
#end //Ende des Makros
Mache_rahmen(3.1) //Makro aufrufen
Creation of trochoids
The following GIF animation shows the formation of a trochoid when a small circle rolls on a large circular line.
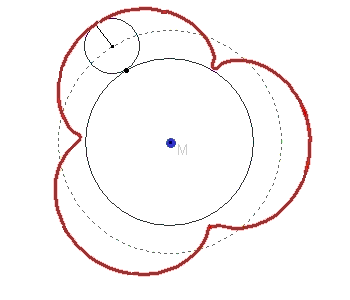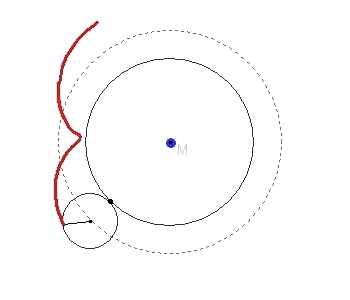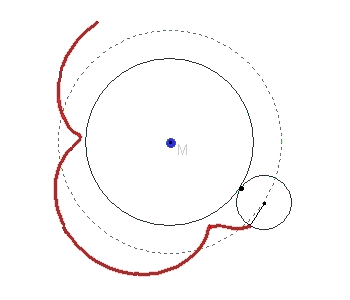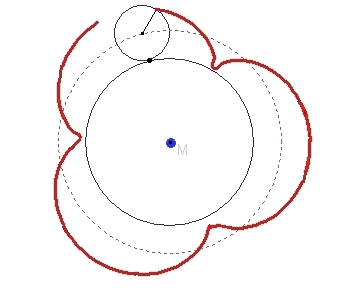
|
| © 2009-2025 Asti | PoVRay-Site |