Gewöhnliche Differentialgleichungen

Hat man eine Beziehung zwischen einer einzigen unabhängigen Veränderlichen x, einer Funktion y von x und einem oder mehreren Differentialquotienten von y nach x, so spricht man von einer gewöhnlichen Differentialgleichung:

f(x, y', y'', y''', ...) = 0

Als Ordnung einer Differentialgleichung wird dabei die Ordnung der höchsten vorkommenden Ableitung bezeichnet.

Differentialgleichungen 2-ter Ordnung kommen besonders oft in der Mechanik vor:
Ist beispielsweise ein Massepunkt durch seine 3 Raumkoordinaten bzw. durch seinen Ortsvektor



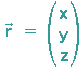
gegeben und ist die unabhängige Variable die Zeit t, dann gilt für die Bewegung des Punktes die Beziehung



Bewegt sich P geradlinig, so gilt für den in der Zeit t zurückgelegten Weg s die folgende Differentialgleichung 2-ter Ordnung:



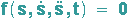
Diese kann als System von 2 Differentialgleichungen 1. Ordnung umgeschrieben werden, indem man die Geschwindigkeit v einführt:



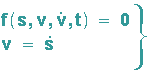
Allgemein kann eine DGL n-ter Ordnung durch ein System von n DGLn 1. Ordnung ersetzt werden, was für das Lösen häufig vorteilhaft ist.