Einfache Anwendungen gewöhnlicher Differentialgleichungen
Freier Fall - Schiefer Wurf: Ein Anfangswertproblem
Gesucht: s = s(t)
Gegeben: 
Da die 2. Ableitung von s konstant ist, muss die Lösung dieser DGL ein Polynom 2. Grades sein:
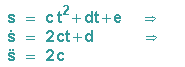
Als Anfangsbedingung wählt man s=s0 für t=0.
Daraus ergibt sich e = s0.
Weiterhin sei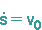 
für t = 0, woraus sich d = v0 ergibt.
Es gilt außerdem noch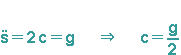 
, sodass man insgesamt die folgende Lösung erhält:
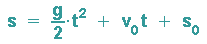
Wählt man nun noch s0=0 und v0=0, so hat man die reine Fallbewegung:
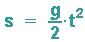
Oberfläche einer rotierenden Flüssigkeit
Gerät eine Flüssigkeit ins Rotieren, so wirken auf einen Punkt P mit der Masse m zwei Kräfte: (vgl. nachfolgende Abbildung)
- Die Schwerkraft
- Die Zentrifugelkraft
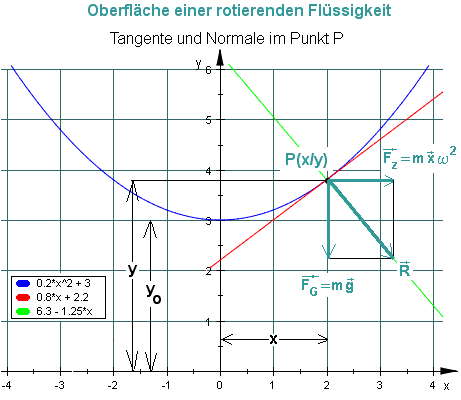
Damit sich der Punkt P im Gleichgewicht befindet und keine Verschiebung der Oberfläche stattfindet, muss die Resultierende von Zentrifugal- und Gewichtskraft auf der Oberfläche senkrecht stehen. Aus dieser Bedingung kann nun die Tangentensteigung im Punkt P und damit auch y' berechnet werden:
Die Tangentensteigung mt = y' ist der negative reziproke Wert der Normalensteigung mn.
Anhand des Steigungsdreiecks der Normalen erkennt man:
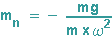
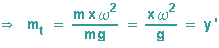
Die Lösung muss also ein Polynom 2. Grades sein, das kein lineares Glied enthält, da y' keine Konstante hat.
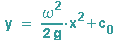
Setzt man y0 = c0 für x = 0, dann ergibt sich das ff. Drehparaboloid:
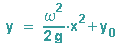
... und um es zu sehen, braucht der Mensch keine Zentrifugalmaschine, ein einfacher Suppentopf mit Inhalt genügt.
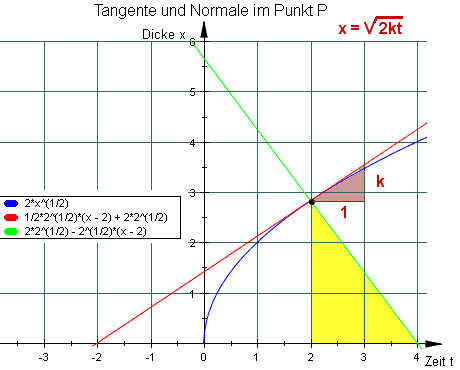
Die Dicke einer Silberjodidschicht
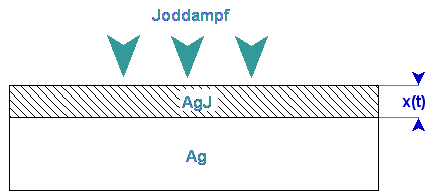
Gelangt Joddampf auf eine Silberplatte, so wächst die entstehende Schicht aus Jodsilber umso schneller, je mehr "unverbrauchte" Ag-Atome zur Verfügung stehen. Mit zunehmender Dicke wird die Wachstumsgeschwindigkeit kleiner. Geht man von der physikalischen Hypothese aus, dass sie umgekehrt proportional zur Dicke x(t) der Schicht sei, dann gilt für die Wachstumsgeschwindigkeit die ff. DGL:
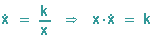
Die Subnormale ist also konstant (siehe auch hier)
und die Dicke x(t) nimmt proportional zur Wurzel aus der Zeit zu:
| © 2009 Asti | Links für Unterricht | PoVRay-Site |