Aufgabe 22:
Programmiere ein rechtshändiges Koordinatensystem
und eine dazu passende Kamera. Lies zunächst den erklärenden Text unter
den Abbildungen!
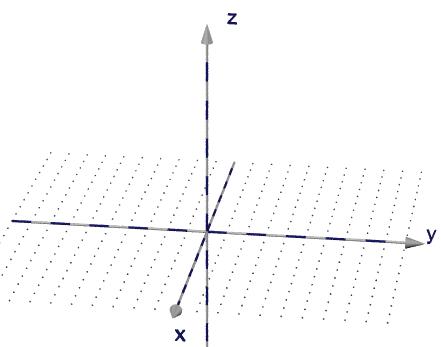
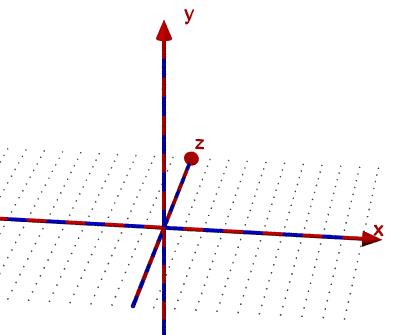
Vergleicht man das rechtshändige Koordinatensystem (obere Abbildung) mit
dem linkshändigen (untere Abbildung), so erkennt man, dass
die
| x-Achse zur y-Achse |
| y-Achse zur z-Achse |
| z-Achse zur -x-Achse |
wird.
Natürlich ist es einfacher, schlichtweg aus der z-Achse die
minus-z-Achse zu machen. Man hat dann jedoch Mühe, Kamera und
Lichtquellen so zu positionieren, dass man Abbildungen erhält, die den
gängigen Darstellungen in den Mathebüchern zu Vektorgeometrie und
linearer Algebra entsprechen.
Wir nehmen also einfach das "alte" Koordinatensystem und beschriften es
"falsch". Um Verwechslungen zu vermeiden, wähle eine andere Farbgebung!
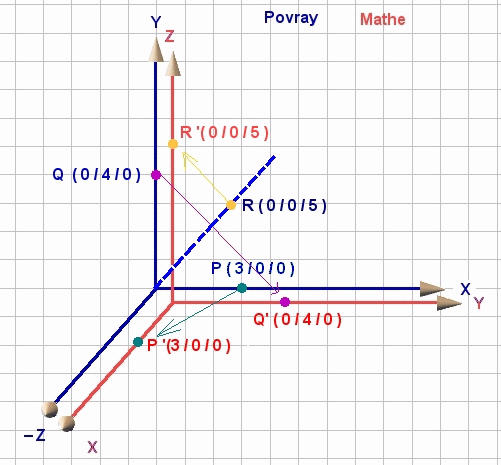
An der obigen Abbildung erkennt man,
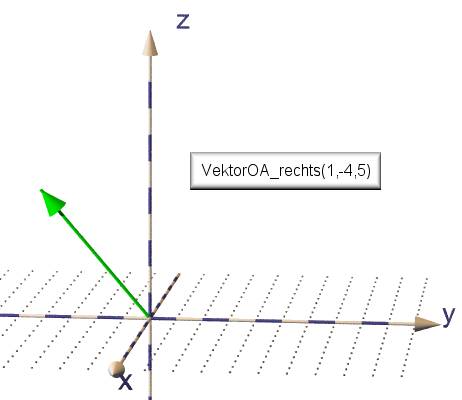
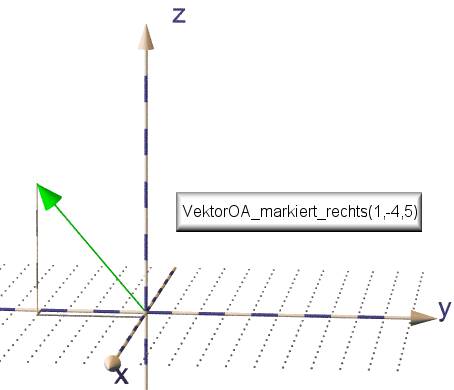
.... dass der Punkt P(3/0/0)von PovRay an der "mathematischen y-Achse"
(d.h. im rechtshändigen Koordinatensystem) gezeichnet wird,
..... dass der Punkt Q(0/4/0) von PoVRay an der "mathematischen z-Achse"
gezeichnet wird,
..... dass der Punkt R(0/0/5) von PoVRay an der "mathematischen
minus-x-Achse" gezeichnet wird.
Für die "mathematischen" Koordinaten gilt also:
Da dem jeweiligen Makro die Variablen x p , y p
und z p übergeben werden sollen, werden die mit 'neu'
indizierten Variablen wieder umbenannt:
Für alle Punkte P(xp/yp/zp), die in den bereits fertiggestellten Makros
auftauchen, musst du nur noch die folgenden lokalen Variablen
definieren, das jeweilige Makro umbenennen, und schon kannst du auch
3-dimensionale Darstellungen entsprechend den Darstellungen in den betr.
Mathebüchern programmieren.
#local x_neu=yp;
#local y_neu=zp;
#local z_neu=-xp;
#local xp=x_neu;
#local yp=y_neu;
#local zp=z_neu;
Wenn wir später Makros programmieren, die bereits vorhandene Makros für
das rechtshändige Koordinatensystem benutzen, müssen überall vor
Makroende diese Transformationen rückgängig gemacht werden. ... Aber
lassen wir das für später!
Als Kamera_rechts bietet sich die ff. Kamera an:
#declare Kamera_rechts = camera {
angle 10
location <20 ,55 ,-135>
right x*image_width/image_height
look_at <0 , 3 ,0>
}
In den nun folgenden Abbildungen ab Aufg. 23 wurden die ff.
Lichtquellen benutzt:
light_source{<25,250,-150> color Gold*1.2}
light_source{<-25 ,5 ,-15> color White*1.8}
Aufgabe 23:
Programmiere nun die zu den ff. Abbildungen
gehörenden Makros und binde sie in deine Geometrie.inc-Datei ein.
Fertige auch die entsprechenden Abbildungen und binde alles mit
passendem Text in ein HTMl-Dokument ein.
... und als Abschluss noch ein Polygon. Programmiert man sich mit Hilfe
des triangle-Befehls ein Makro Dreieck_rechts, dann kann man über die
Farbgebung auch gut verdeutlichen, dass vier gegebene Punkte nicht in
einer Ebene liegen: