- Grundlagen
- Zusatzinfos zu Aufgaben
- Aufgaben 1 - 21
- Aufgaben 22 - 23
- Ebene in Normalenform
- Startseite Geometrie
- Startseite PoV-Theorie
- Startseite
Das Ziel:
Es soll eine Include-Datei "Geometrie.inc" entstehen, in der
Deklarationen oder Makros zur Verfügung gestellt werden, mit denen dann
Elemente aus der analytischen Geometrie (die Ihr in Mathe 12
kennenlernen werdet) problemlos programmiert werden können.
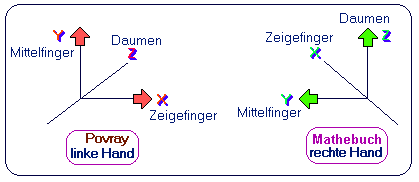
Leider gibts einen Unterschied: PoVRay hat ein linkshändiges
Koordinatensystem (linker Daumen zur x-Achse, Zeigefinger zur y-Achse,
dann gibt der zu beiden rechtwinklig ausgestreckte Mittelfinger die
z-Achsen-Richtung an. In der Mathematik wird i. a. ein rechtshändiges
Koordinatensystem benutzt.
-
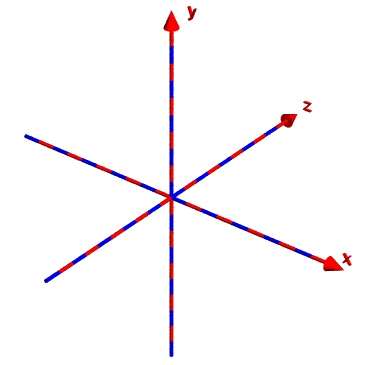
Koordinatensystem mit Beschriftung x, y und z und 2-farbig als
Achsenskalierung
Rasterebene
Rasterpunkte
Punkt
Vektor
Gerade (2-dimensional) in Hauptform
Gerade (2-dimensional) in 2-Punkte-Form
Gerade (2-dimensional) in Punkt-Steigungsform
Schnittpunkt zweier Geraden (2-dimensional)
Gerade in Punkt-Richtungsform
Gerade in Punkt-Normalenform
Ebene in 3-Punkte-Form
Ebene in Punkt-Normalenform
Ebene in Koordinatenform
Ebene in Achsenabschnittsform
----- wenn's bis hier gelingt, ist's schon mal SPITZE!!! -------
Dann wäre alles noch fortsetzbar: (ist von der Theorie her natürlich ab Mathe12, 2. Halbjahr einfacher lösbar!)
-
Schnittpunkt zweier Geraden (3-dim.)
Spurpunkt (=Schnittpunkt) von Geraden mit den 3 Grundebenen
-
Spurgerade (=Schnittgeraden) von Ebenen mit den 3 Grundebenen
Schnittgerade zweier Ebenen
Aufgabe 1:
Programmiere die Datei Koord.pov, die folgendes oder ein ähnliches Bild liefert: Verwende dazu die Startdatei und sichere sie unter dem neuen Namen. Stelle die Position der Kamera geeignet ein.
 |
.. und schon gibt's ein Problem:
Der Text-Befehl für Windows lautet
text { ttf "arial.ttf", "y", 0.15, 0 pigment{Red} translate <1,11,0>}
Hier der Auszug aus der Windows-PovRay-Hilfe:
TEXT_OBECT:
text {
ttf "fontname.ttf/ttc" "String_of_Text"
Thickness,
[OBJECT_MODIFIERS...]
}
Der zugehörige Windows-TrueTypeFont wird dann ins jeweilige Arbeitsverzeichnis kopiert oder mit dem Pfadnamen aufgerufen. Falls es unter einem anderen Betriebssystem keine TrueTypeFonts gibt, dann aus dem Internet einen passenden Font runterladen.
Zum Einfärben der Achsen kann modulo benutzt werden.
- Es gilt: 17 : 5 = 3 Rest 2
- Es gilt also: 17 mod 5 = 2
- Lässt man also einen Zähler die Werte 1 bis 100 annehmen und fragt, ob zaehler mod 10 = 0, so erhält man die Vielfachen von 10, wenn die Antwort "ja" ist.
Denn: 10 mod 10 = 0, 20 mod 10 = 0, .... - Für die Syntax von mod gilt: mod (zahl1,zahl2)
Aufgabe 2:
Öffne eine leere Pov-Datei und sichere sie unter dem Namen geometrie.inc in dein pov-Arbeitsverzeichnis.
Schreibe dort Folgendes hinein:
// ==== Standard POV-Ray Includes ====
#include "colors.inc"
#include "textures.inc"
#declare Kamera01 = camera {
angle 10
location <80 ,80 ,-100>
right x*image_width/image_height
look_at <0 , 1 ,-0.5>
}// Ende der Kamera
Lösche nun in der Datei koord.pov die camera-Zeilen, schreibe stattdessen Kamera01 hin. Ergänze im Programmkopf #include "geometrie.inc". Alles sollte (von der Kameraposition, die du evtl. in der Include-Datei anpassen musst, genauso funktionieren! Den Sehwinkel kannst du auch verändern.
Anmerkung:
Arbeitet man z. B. mit Pyvon als Programmierumgebung zu PoVRay unter Linux, dann werden die include-Dateien nicht mit angeboten, sie müssen also getrennt aus dem Internet (mit einer Windows-Version) runtergeladen und in's home-Verzeichnis kopiert werden.
Aufgabe 3:
Programmiere unter Verwendung einer geeigneten Zählschleife eine "Rasterebene" aus 21 Reihen von je 21 Kügelchen, sodass die Koordinatenachsen von -10 bis -10 in der x-z-Ebene ein Raster haben. Dateiname: raster01.pov.
 |
Aufgabe 4:
Öffne die Datei geometrie.inc und ergänze sie:
#declare koordxyz=object{
... hier wird dein Koordinatensystem aus koord.pov eingefügt ...
}//Ende des Koordinatensystems
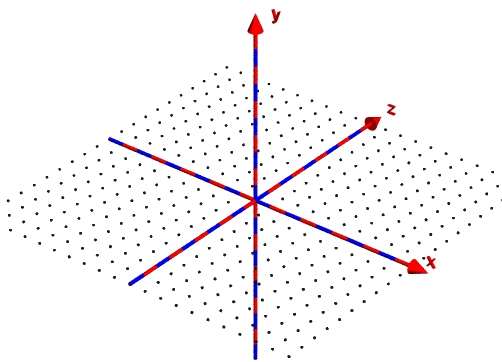
Schreibe in die Datei raster01.pov nun in den Verarbeitungsteil koordxyz dazu. Das Ergebnis sollte wie folgt aussehen:
 |
Aufgabe 5:
Lagere nun deine Rasterpunkte ebenfalls in die geometrie.inc-Datei aus:
#declare Rasterpunkte=object{
union{
..... deine Zählschleifen....
}//Ende der Vereinigungsmenge
}Ende des Objekts
In der Datei raster01.pov steht im Verarbeitungsteil -zusätzlich zur Lichtquelle -nur noch:
Kamera01 koordxyz Rasterpunkte
Die zugehörige include-Datei hast du ja schon eingebunden, oder ?????????
Aufgabe 6:
Programmiere noch eine zweite Datei raster02.pov, deren Raster in der xz-Ebene aus dünnen Zylindern besteht.
Aufgabe 7:
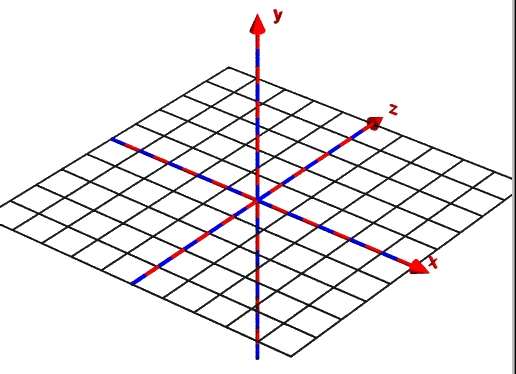
Lagere dieses Raster nun auch unter geeignetem Namen in deine include-Datei aus und rufe es dann mit diesem Namen in raster02.pov auf.
So etwa sollte es aussehen.
 |
Für die kommende Aufgabe ist die Verwendung eines Makros nötig:
#macro Punkt (xp, yp, zp) .......... Anweisung zur Ausgabe des Kügelchens........ #end
Mit Punkt (3,-5,6) wird der Punkt dann auch im Bild ausgegeben.
Die Anzahl der Parameter in der runden Klammer muss mit der Anzahl der Parameter anzahlmäßig und namentlich übereinstimmen!
Falsch für das obige Makro wäre: sphere {<a,b,c> 0.3 pigment {Farbe}}
Für eine solche Anweisung wäre die ff. Kopfzeile nötig: #macro Punkt (a,b,c,Farbe)
Aufgabe 8:
Jetzt geht's an die Punkte: Alles was ihr zunächst mal braucht sind kleine bunte Kügelchen in gut sichtbarer Farbe (Farbnamen kannst du dir in der Datei colors.inc aussuchen), deren Mittelpunkt dort ist, wo der Punkt sein soll. Dateiname: punkt01.pov.
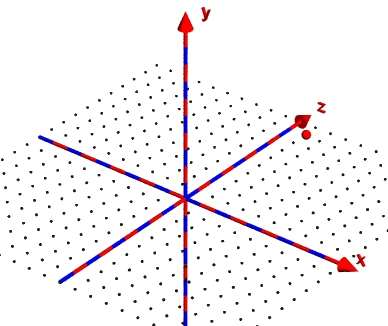 |
Im Beispiel ist der Punkt p(4/3/5) dargestellt, was natürlich schlecht zu erkennen ist.
Also: Verbesserung ist angesagt:
Aufgabe 9:
Das Ergebnis der Datei punkt02.pov sollte so aussehen: Die Ablesbarkeit der Koordinaten in der xz-Ebene ist schon mal gut, an der Ablesbarkeit in der y-Richtung muss noch gearbeitet werden.
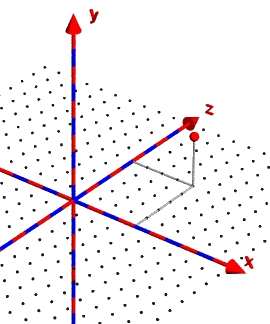 |
Aufgabe 10:
Ändere also deine Punkt-Programmierung, bis du ein Ergebnis hast, bei dem alle Punktkoordinaten deutlich ablesbar sind:
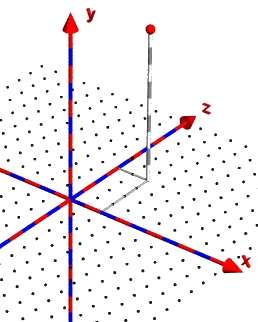 |
Aufgabe 11:
Überprüfe nun dein Ergebnis, indem du einen Punkt mit negativen Koordinaten anzeigen lässt. Hast du etwa eine Endlosschleife programmiert? Hast du möglicherweise eine if-Abfrage ausgelassen? Falls nötig verbessere, bis du ein gutes Ergebnis hast.
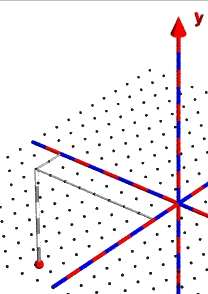 |
Verschwinden evtl. deine Punkte unter einer undurchsichtigen xz-Ebene?
Und hier noch ein Tipp zur Aufgabe 11:
mit abs(Zahl) wird der Absolutbetrag einer Zahl bestimmt, also abs(-8) = 8.
Aufgabe 12:
Überprüfe nun deine Kameraposition, sodass alle Punkte von P(-10/-10/-10) bis Q(10/10/10) auch im Bild sichtbar bleiben.
Eine Möglichkeit (noch zu verbessern) ist die Abbildung.
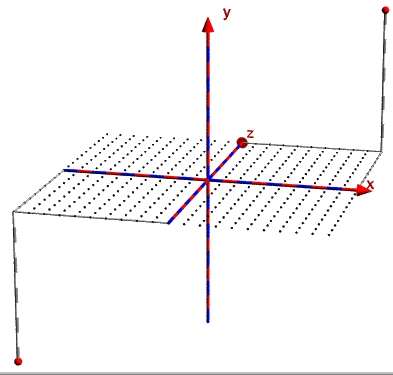 |
camera {
angle 15
location <30 ,35 ,-120>
right x*image_width/image_height
look_at <0 , 0 ,0>
}
Aufgabe 13:
Wie sieht's in deinem Arbeitsverzeichnis aus?? Lege ein Unterverzeichnis GEOHTML an und kopiere geometrie.inc dorthin und ein PoV-Skript mit dem Namen geometrie.pov.
In dieses schreibst du den Programmkopf mit den nötigen include-Dateien, auch dein Name kann hier mal auftauchen. Der Deklarationsteil bleibt leer, alles Nötige ist ja in geometrie.inc. Im Verarbeitungsteil stehen alle Makros oder Objekte, die in geometrie.inc deklariert sind, jeweils alle außer einem auskommentiert. Dazu ein kleiner Kommentar über ihre Verwendung. Natürlich auch eine oder zwei Lichtquellen.
Das Koordinatensystem und die Rasterpunkte sind nicht auskommentiert.
Fertige nun kleine Beispielbilder im Format 320x240 Pixel, png- oder jpg-Grafik, sodass für jedes Makro oder Objekt ein Bild zur Verfügung steht. Im HTML-Dokument geopov.html gibt es einen Link zu Geometrie.inc und zu geometrie.pov. Zu jedem Bild ein kleiner Kommentar.
Aufgabe 14:
Als nächstes soll ein Vektor vom Koordinatenursprung zu einem gewünschten Punkt A(xa/ya/za) programmiert werden.
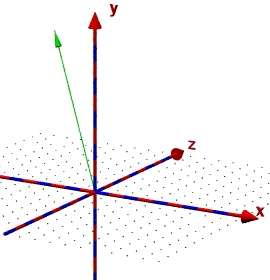 |
Hier gibt's gleich zwei Probleme:
- die Komponenten des Vektors ,im Beispiel , sind schlecht erkennbar,
- ein kleiner Kegel für die Pfeilspitze muss dieselbe Richtung wie der Vektor haben.
Fangen wir mit der Pfeilspitze an:
benötigt wird die Funktion vnormalize(<xa,ya,za>)</xa,ya,za>, die aus dem Vektor einen Vektor der Länge 1 LE macht, der dieselbe Richtung wie hat.
Beispiele zu vnormalize(<xa,ya,za>):
VektorOA(7,10,3)
Punkt(7,10,3)
sphere {vnormalize (<7, 10,3>) 0.3
pigment{Blue}
}//Ende Kugel
liefert das Bild rechts:
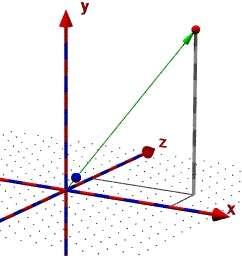 |
Die kleine blaue Kugel liegt auf der Verbindungslinie vom Ursprung zum Punkt (7,10,3) und hat vom Ursprung den Abstand 1 LE.
cone{<0,0,0> 0.2 vnormalize(<7, 10, 3>) 0
pigment {Blue}
}// Ende Kegel
liefert einen kleinen Kegel der Höhe 1 LE, der dieselbe Richtung wie der gewünschte Vektor hat. Er muss nun nur noch verschoben werden. Macht man dies mit translate <xa, ya,="" za=""> , dann ragt seine Spitze über den Punkt A hinaus, bei der Verschiebung muss also noch vnormalize(<xa,ya,za>) subtrahiert werden!
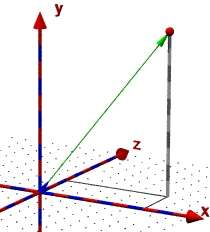 |
So, die Datei vektor01.pov ist kein Problem mehr. Wenn alles klappt, dann lagere das Makro gleich zu geometrie.inc aus, und rufe es in vektor01.pov auf.
Zum Testen der Pfeilspitzen gib die ff. 3 Vektoren ein:
VektorOA(6,10,3)
VektorOA(1,8,7)
object {VektorOA(6-1,10-8,3-7) translate <1,8,7> }
Das Ergebnis sollte der Abbildung rechts entsprechen!
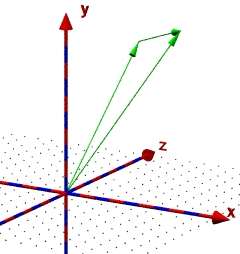 |
Aufgabe 15:
Als nächstes soll ein Vektor vom Punkt A(xa/ya/za) zum Punkt B(xb/yb/zb) programmiert werden.Bezeichnet man in der obigen Abbildung die beiden Spitzen der langen Vektoren mit A und B, dann erkennt man, dass
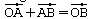
ist, es gilt also
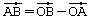 .
.
Programmiere nun also das Makro VektorAB (xa,ya,za,xb,yb,zb) , binde es in geometrie.inc ein und rufe es in deinem pov-Skript auf.
Aufgabe 16:
Es war ja nicht anders zu erwarten, die Komponenten sollen ablesbar sein: So wie in der Abbildung oder schöner soll das Ergebnis sein. Im Beispiel ist
A (-4 / -9 / 2) und B(7 / 8 / 6)
erkennbar, oder ?
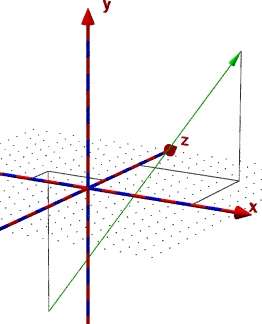 |
Überprüfe für "ausgefallene" Punkte, ob der cylinder-Befehl möglicherweise eine Fehlermeldung liefert: base point = apex point (d.h. Grundkreismittelpunkt und Deckkreismittelpunkt sind identisch).
Mit vlength (<xa,ya,za>) >0 (Bestimmung der Länge des Vektors ) kannst du eine if-else-Abfrage einbauen: wenn bei den Markierungen die y-Komponente 0 ist, soll eine kleine Kugel gezeichnet werden.
Weiter geht's zu den 2-dimensionalen Geraden.
Aufgabe 17:
Die Darstellung einer Geraden in der Hauptform y = mx + b, als Makro programmiert. a) Eine sinnvolle Kamera ist
#declare Kameraxy = camera {orthographic
angle 20
location <0 ,0.01 ,-95>
right x*image_width/image_height
look_at <0 ,0 ,0>
}
wobei das Schlüsselwort orthographic die Kamera anweist, parallele Lichtstrahlen zur Bildentstehung anzuwenden.
b) Ein xy-Koordinatensystem muss her.
c) "Kästchenpapier" für die xy-Ebene brauchen wir auch.
d) Rufe nun das Makro GeradeHauptform (m,b) auf.
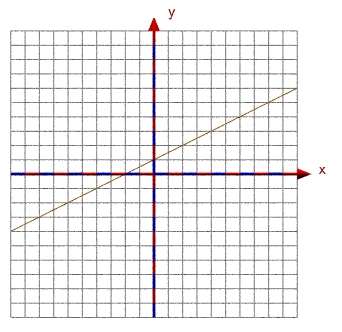 |
Raster_xy koordxy_markiert GeradeHauptform (0.5,1)
sollte ein Ergebnis wie die Abbildung oben liefern:
Aufgabe 18:
Für die Gerade in der 2-Punkte-Form
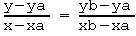
bietet sich natürlich ein Zylinder von einem Punkt zum nächsten an. Liegen die beiden Punkte jedoch dicht beieinander, dann ist das Ergebnis nicht schön. Auch in diesem Fall soll die Gerade von x1 = -10 bis x2 = +10 dargestellt werden.
Zwei Lösungen bieten sich an:
- Aus den gewünschten Punkten werden die y-Werte für x1 = -10 und x2 = +10 berechnet, dann ein Zylinder gezeichnet.
- Aus den gewünschten Punkten werden die y-Werte für m und b
berechnet, dann ein Zylinder gezeichnet analog zur Aufgabe 15.
Die Abbildung rechts ist aus der ersten Möglichkeit entstanden.
Aufgabe 19:
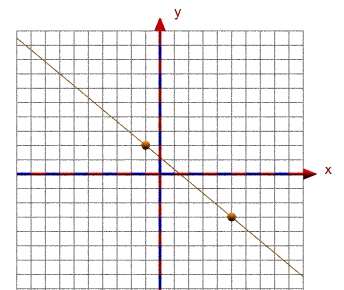
Was noch fehlt, ist eine Gerade in der Punkt-Steigungs-Form:
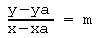
Das aufgerufene Makro GeradePS (1,-4,2.5) sollte die ff. Abbildung liefern.
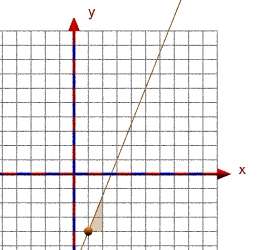 |
Denke auch an das Steigungsdreieck! Es wird mit dem Befehl
triangle {
<...,...,...>
<...,...,...>
<...,...,...>
pigment {color Coral transmit 0.6}
}// end triangle
berechnet.
Die drei Eckpunkte kannst du leicht aus der Geradengleichung berechnen.
Mit dem Schlüsselwort transmit nach Coral wird diese Farbe zu 60% transparent gemacht.
Aufgabe 20:
Wird sind bei der Schnittpunktbestimmung zweier 2-dimensionaler Geraden angelangt. Damit das Thema 2-dimensionale Geraden nicht zu umfangreich wird, beschränken wir uns auf den Fall, dass die Gerade in der Hauptform gegeben ist. Der Schnittpunkt kann dann durch Gleichsetzen berechnet werden.
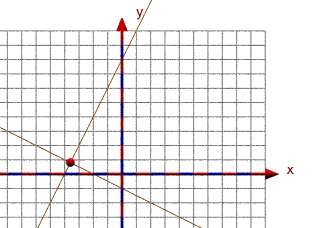 |
Schnittpunkt(2, 8, -.5,-1) wurde abgebildet.
Aufgabe 21:
Die Ausgabe der Koordinaten soll noch ergänzt werden. Wenn innerhalb des Makros mit
#local xs = ...........;
der Wert einer Variablen deklariert wurde, dann kann diese mit
str (string)
in eine Zeichenkette umgewandelt werden und mit
text{ttf "cyrvetic.ttf",str(xs,3,2),0.25, 0 pigment{.... }}
im Schnittpunktmakro eingefügt werden. Die Zahl 3 im Beispiel gibt die Mindestlänge der Zeichenkette an, die 2 die Anzahl der Nachkommastellen (abgeschnitten, nicht gerundet). Mit einer Verschiebung soll die Ausgabe an einer geeigneten Stelle platziert werden.
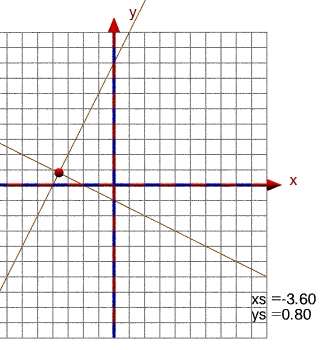 |
| © 2010 Asti | PoVRay-Site | Mathematische Streiflichter | Algorithmische Kunst |