Einführung

Wahrscheinlichkeitsverteilung, Verteilungsfunktion und Wahrscheinlichkeitsfunktion

Die Grundlagen der Wahrscheinlichkeitsrechnung sowie die Zählregeln aus der Kombinatorik werden hier als bekannt vorausgesetzt.

Einführendes Beispiel 1:

Ein Würfelspiel wird mit 2 Würfeln gespielt, jeder Augenkombination (Ergebnis) ist ein Gewinn oder ein Verlust zugeordnet. Man zahlt z.B. einen Euro, wenn keine 6 fällt, für jede gewürfelte 6 erhält man einen Euro. Der Gewinn, die Zufallsgröße X, kann also die Werte +2, +1 oder -1 annehmen.

Den möglichen Werten x_i der Zufallsgröße X sind dann Wahrscheinlichkeiten zugeordnet:

Ordnet man jedem möglichen Wert x_i, den die Zufallsgröße X annehmen kann, die Wahrscheinlichkeit P(X=x_i) zu, dann nennt man dies die Wahrscheinlichkeitsverteilung der Zufallsgröße X.

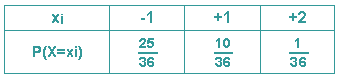
Die Wahrscheinlichkeitsverteilung der Zufallsgröße X ist graphisch darstellbar (häufig auch als Stabdiagramm):

Einführendes Beispiel 2: Einmaliges Werfen zweier Münzen.

Die Zufallsvariable X sei die Anzahl der Wappen. Es gilt also:

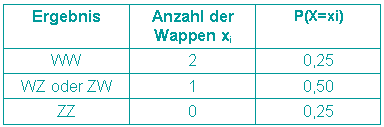
Für die graphische Darstellung der Wahrscheinlichkeitsverteilung gilt also:

Verteilungsfunktion

Betrachtet man zu einer gegebenen reellen Zahl x die Wahrscheinlichkeit

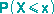, mit der die Zufallsvariable X einen Wert kleiner oder gleich x annimmt, dann erhält man eine Funktion F_x(x), die als Verteilungsfunktion bezeichnet wird.

Für das 2. Beispiel - einmaliges Werfen zweier Münzen - gilt:

Mehr als 2 Wappen sind nicht möglich, weniger als 0 Wappen sind nicht möglich, die Wahrscheinlichkeit für weniger oder gleich 1 Wappen setzt sich aus den Teilwahrscheinlichkeiten zusammen.

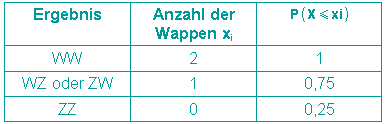
Man erhält die folgende graphische Darstellung:

Wahrscheinlichkeitsfunktion
Wenn x₁, x₂, x₃,... die Werte einer diskreten Zufallsvariablen X mit positiver Wahrscheinlichkeit sind und p₁, p₂, p₃,... die zugehörigen Wahrscheinlichkeiten P(X=x_i)=p_i, dann ist

die Wahrscheinlichkeitsfunktion für X.

PoVRay-Site